ГЛАВА ПЯТАЯ
ТУПОСТЬ И ГЕНИЙ
«Бесконечность — пучина, в которой тонут
наши мысли»
Симон Люилье
«Игра в математику происходит в
полном безмолвии, без единого слова…»
Герман Вейль
«…
не следует слишком удивляться, если попытки описания природы приведут нас в
конце концов к логике, этому «воздушному замку» в самом центре математики.
Если, как считают, вся математика сводится к математической логике, а вся
физика — к математике, то разве не единственной возможностью является то, что
физика сводится к математической логике? Логика — единственная область
математики, которая может «размышлять о себе самой».
Ч. Мизнер, К. Торн, Дж. Уилер «Гравитация»
«Я не знаю более совершенного способа и
сохранить для науки чувственное представление, и в то же время ограничить его в
сравнении с научным понятием […], кроме
толкования понятия как предела и представления как переменной величины,
стремящейся к пределу. … Переменная величина имеет предел, говорят
математики, если разница между ней и ее пределом может стать меньше любой
заданной величины, т.е. вечно стремится к нулю. Что этим чувственное
представление буквально спасается для
науки, это совершенно ясно. Вместо расплывчатого пятна неизвестно чего, вместо
абсолютной текучести дряблого чувственного марева представление получает определенную закономерность, оно
получает научный смысл, его уже нельзя просто отбросить, оно — настоящий
фундамент науки. Но в то же время все его логическое значение держится, по
нашей теории, только его пределом, т.
е. понятием, общим, которое им
управляет, как в математике предел управляет соответствующей ему переменной
величиной. В этом пределе нет ровно ничего таинственного или
сверхъестественного. Это—самая обыкновенная конечная величина».
Алексей
Фёдорович Лосев («Хаос и структура»)
«Тупость и гений»… Так назвал свою статью академик АН
СССР А. Д. Александров, в которой он подробно рассказывает о трудном и
противоречивом пути становления неевклидово геометрии, являющейся одной из
заявленных в предыдущей Главе математических форм диалектического движения человеческой
мысли, которая в философии была выражена и известна как спекулятивный
философский метод Ф.Гегеля.
И хотя рассмотрение всех математических форм мы будем
производить в строго заявленном порядке,
то есть черёд неевклидовой геометрия наступит лишь в конце настоящей Главы, её
начало справедливо венчает неотделимая друг от друга пара «гениальность –
тупость».
Впрочем, если вдуматься разве гениальность это высшая мера развития человечности?
Нет. Скорее наивысшая мера явления духа человека – в
человеке, в котором и несломимое мужество, и упорство, и абсолютная
независимость от мнения и точек зрения иных, и умение прежде всего найти в
самом себе необходимое духовное основание, на котором только и можно устоять в
воистину страшном противостоянии … всемирной
тупости – тупости как активности
потенциала сил тьмы и зла.
История становления
неевклидовой геометрии в этом отношении весьма и весьма показательна и
поучительна.
Тупые – безымянные толпы армии тьмы!
Тупость – обезличенная личина зла!
Тупоумие – основа основ всех мыслимых и немыслимых
форм тирании над человечностью, демонстрируемых самим человечеством!
Демонстрируемых и допускаемых Всеобщим («Богом») с единственной целью – показать как можно ярче и отчетливее всему тупому человечеству вместе и
каждой его частице в отдельности его омерзительную
тупость!
Для чего?
Да чтобы помочь, побудить, заставить человека мыслить.
***
Итак,
начнём наше движение.
Кажется
Рене Декарт сказал, что нельзя придумать ничего столь странного и невероятного,
что не было бы уже высказано кем-либо из философов. И это действительно так,
это – правда.
Глава
Пятая и посвящена такого рода правде, а точнее – истине спекулятивной
гегелевского философии, спекулятивный характер которой означает лишь опору этой философии на бесконечное, а истинность – её всеобщность,
всепроникающий свет которой мы будем искать и находить в пространстве математики.
Предмет
нашего исследования: «философия и математика» – предмет, который кажется и необозримым, и неисчерпаемым. Но истины ради необходимо отметить,
что число тех, кто достоин звания «философа» в столь специфической области математики вполне хватит пальцев одной руки.
Один
из них и по всей очевидности достигший самых
выдающихся результатов - Алексей Федорович Лосев.
Ранее
уже было отмечено, что если наблюдать философию под предельно острым
диалектическим углом зрения, который как раз и легко позволяет увидеть тех, кто
на голову, а то и на две выше всех остальных, то создаётся стойкое впечатление,
что все иные философы делают вид, что
никакого Лосева в истории философии вовсе не было, как не было и всего того что
им написано в отношении того, что составляет саму сущность философского видения
– её метод – диалектику.
Философские
работы и исследования Алексея Федоровича Лосева, которые мы используем, написаны им в 30-40-х годах прошлого века и,
как указано в послесловии к книге «Хаос и структура» (где они представлены), изданной
в 1997 году, «ни одно из них не знало печатного станка при жизни автора».
Казалось
бы, четырнадцатилетний период является вполне достаточным для ознакомления даже
с учетом всей неповоротливости мысли философских масс, но нет, их вероятная
задумчивость всё длится, длится и длится многозначительной тишиной, которую просто необходимо прервать, та как она уже
неотличима от тишины склепа.
И
видимо весьма трудно выделить какую-то одну или даже несколько причин такого
положения дел, если вообще возможно,
но скорее всего она имеет кроме, разумеется, глубинной и законной – единой меры зрелости всеобщей философской
мысли и чисто психологические.
И потому Алексей Федорович Лосев – скромный русский гениальный
философ вроде бы и есть, но фактически его, увы, нет, и эта нелепая антиномия, венчающая тупость и
трусливость мысли всех тех, кто мог бы увидеть правду и сказать о ней всем, но
не хочет видеть и боится её, – вопиёт,
но вопиет, как всегда, когда люди имеют дело с пророками – в пустыне, пустыне человеческой глупости:
«.. автор считает необходимым сказать, что его
инфинитезимальная логика является пока только скромным предложением и что она нуждается в подробной
и внимательной критике со стороны
советских философов. Возможно, что здесь окажется многое неверным или излишним
и что это предложение потребует в дальнейшем коренной переработки. Однако все
это является только вполне естественным, поскольку данное предложение и связанное с ним исследование являются новыми,
ибо безопасным является только повторение старых трафаретов. Автор, во всяком
случае, вдохновлялся известными словами товарища Сталина, что «овладеть
марксистско-ленинской теорией—значит уметь развивать ее и двигать вперед»».
Подобно
тому, как
для западного и особенно звездно-полосатого обывателя всё то, что произносится и исходит из определенного источника, или
имеет к нему некое отношение, источника априори имеющего (как он полагает) прямое
отношение к злу, например, киношного злодея-террориста, не может быть истинным и
быть правдой.
Так и обыватели от философии влившиеся,
наконец, «в единую всемирную философскую семью», ныне случайно наткнувшись на словосочетания
вида «тов. Сталин», «Владимир Ильич Ленин», «марсксизм-ленинизм»
останавливаются в ужасе и, не желая «переходить на тёмную сторону», откладывают
в сторону произведения, где содержится подобная философская бесовщина.
Но Алексей
Федорович Лосев в нечеловеческих условиях торжества лагерного сталинского «социализма», лагерного не в переносном, а в прямом
смысле, двигал
и двигал вперёд диалектику, и делал это настолько успешно и умело, что
глядя из сегодняшнего дня его реверансы в сторону «советских философов» кажутся
и нелепыми и даже унижающими.
Итак, время представить новый материал, точнее, его часть, который и станет основой, с
которой мы и начнём процесс обозрения пространства заявленной ранее сферы,
сферы бесконечно малого, бесконечно большого и понятия предела неразрывно
связанного с бесконечностью, которую человеческий
ум решается охватить и становится в таком движении разумом. Кроме того,
нельзя не отметить, что знания добытые А.Ф.Лосевым по настоящий момент являют собой великолепный учебный материал к которому, как правило, мало что
можно добавить:
«1. Бытие, небытие, становление. Приступая
к логическому анализу всех основных категорий, оперирование с которыми создает
науку математического анализа, мы должны помнить, что далеко не все, понятное
математически, тем самым является понятным и с философской точки зрения. Часто
бывает так, что математик ограничивается каким-нибудь очень коротким
разъяснением или формулой, философ же затрачивает массу времени и пространства,
чтобы эту короткую и простую формулу разъяснить для себя и понять. Точно так же
нередки и случаи, когда весьма пространные математические выкладки для философа
не имеют почти никакой цены и из массы доказательств важной оказывается только
какая-нибудь одна идея. Тем не
менее давно уже настало время, когда математический анализ требуется понять
широко философски и ощущается насущная потребность вывести его из
формалистического тупика и пустой, бессодержательной трактовки.
Мы рассмотрим ряд категорий, приводящих к самому
понятию бесконечно-малого, потому что понятие это с логической точки зрения
довольно сложное и те определения, которые мы имеем в руководствах по анализу,
для нас слишком формалистичны и техничны. Они
совсем не вскрывают ту логическую структуру, которая кроется в понятии
бесконечно-малого.
Мы
начнем с тех трех категорий, с той общезначимой диалектической триады, без которой невозможно вообще никакое логическое построение, и каждое логическое
построение есть только вид этой триады, один из бесконечно разнообразных ее
случаев. Это та триада, с которой начинается всякая диалектика:
1)
бытие,
2)
небытие (инобытие),
3)
становление.
Тут
прежде всего — бытие.
Почему диалектика начинается с бытия?
Потому что всё, всякая категория, прежде чем быть самой собой, должна просто быть. Прежде чем быть чем-нибудь и как-нибудь, надо сначала просто быть.
Вот почему диалектика, желающая дать всю область знания в системе, необходимым
образом начинает с «бытия». Бытие—первый шаг, первый жест, первое движение, первая
точка диалектики. Без этой точки, без этого первоисточника никакое построение
невозможно.
Далее,
бытие не может остаться только бытием, просто бытием. Бытие не есть бытие вообще. Если бы оно всегда оставалось
бытием вообще, мы никогда не смогли бы получить никаких конкретных форм бытия. Существует не просто
бытие, но и разные виды бытия. А для
этого нужна такая универсальная категория, которая бы сделала возможным
существование этих разных видов бытия. Такой категорией является инобытие, т. е. иное, другое бытие, являющееся по отношению к первому общему бытию отрицанием его, отсутствием его,
небытием. Как только мы положим бытие,
так тут же необходимо полагать и небытие,
это понятия соотносительные. Если есть черный цвет, то
он может быть только тогда, когда есть (или по крайней мере мыслится) не-черный
цвет.
Если мыслится белое, значит, как-нибудь и где-нибудь
существует «не-белое». Также и «бытие», если оно
реально есть или мыслится, то тем самым есть или мыслится «инобытие».
Но стоит
только немного задуматься над той антитезой бытия и небытия, как становится
совершенно ясно, что остаться при такой антитезе совершенно невозможно. Если
оставить эти две области бытия и небытия в их голой и абсолютной
противоположности, то совсем не будет достигнута цель, ради которой мы и ввели
понятие инобытия. Мы ввели его для того, чтобы вместо абстрактного и общего
бытия получить его конкретные виды. Но если инобытие будет абсолютно оторвано
от бытия и не будет как-то с ним совмещено,— не возникнет и никаких конкретных
видов бытия.
Необходимо
их как-то объединить, эти категории бытия и небытия, как-то нащупать то, что
есть в них общего и что могло бы нейтрализировать этот дуализм двух
противоположных логических стихий. Но что значит найти общее, что значит
объединить? Это значит найти такую новую категорию, где обе полученные уже
содержались бы и где они были бы покрыты чем-то третьим, что их и объединило
бы.
Такой
категорией является становление. В
становлении мы находим прежде всего то, что становится. Стало быть, тут бытие
налично. Но вместе с тем здесь же мы имеем тоже и некое как бы отталкивание от
этого бытия. Становление есть ведь некий процесс, где бытие все время меняется
и переходит в другое. В каждый мельчайший момент своего становления бытие—все
иное, иное и иное. Оно тут никогда не одно и то же. В каждый мельчайший новый
момент бытие оказывается небытием в отношении к прежнему бытию, к бытию в его
прежней форме. И таким образом, в каждый мельчайший момент становления
становление оказывается и бытием, и небытием. Потому в диалектике и говорят,
что бытие и небытие синтезируются в становление.
2. Целое, дробное, бесконечность. Тут мы
пока еще у преддверия анализа бесконечно-малых, но пока еще не вошли в него, не
получили еще самого понятия бесконечно-малого. Попробуем конкретизировать достигнутую нами
диалектическую ступень — с тем чтобы дойти постепенно и до этого понятия.
Первое,
с чем мы тут встретимся,— это понятие и область числа. Когда мы выставляли
указанную диалектическую триаду, мы не имели в виду чисел, а говорили в
применении вообще ко всяким возможным предметам мысли. Теперь необходимо эту же
самую триаду провести в чисто числовой области.
Разумеется,
различных форм приложения этой триады к области чисел очень много. Так, напр., если мы возьмем положительное
число, то антитезой к нему будет, очевидно, отрицательное число, а синтезом, в котором
соединится то и другое, будет, очевидно, нуль.
Но эта триада неинтересна в смысле получения понятия бесконечно-малого, и она
ничего не разъясняет нам в математическом анализе. Потому подробно говорить о
таких построениях надо только в общей философии числа, но не в логике
математического анализа. Что же в числе есть такого, диалектическое понимание
чего приводит нас вплотную к математическому анализу?
Математический анализ есть исчисление
бесконечно-малых.
Стало быть, здесь мы находимся в области учения о
бесконечном.
Спрашивается:
что такое бесконечность?
Самое
простое и самое «понятное» популярному сознанию — это то, что
бесконечность есть нечто, не имеющее конца. Хотя это как будто и ближе всего
передает смысл данного понятия, тем не менее считать это вполне ясным
совершенно невозможно. Как понимать это отсутствие конца? Обычно это понимается
так, что, сколько бы мы ни двигались к границе, мы никогда не можем ее
достигнуть. Другими словами, в понятие бесконечности вносят идею процесса. И это
вполне справедливо, хотя, быть может, и недостаточно. Самое простое и самое понятное — это понимать бесконечность как бесконечный процесс. Однако
этим нисколько задача не решается. Вместо того чтобы определить понятие,
выраженное при помощи существительного («бесконечность»), мы в
данном случае приходим к необходимости определять понятие, выраженное через
прилагательное («бесконечный процесс»). И если мы там не понимаем, что такое
бесконечность, то не станет она понятнее и здесь. Какой же процесс мы должны
считать бесконечным? Вот вопрос, который теперь предстоит нам решить.
Пусть мы
от 1 перешли к 2, от 2 к 3, от 3 к 4 и т. д. Спрашивается: можем ли мы
когда-нибудь на этом пути получить бесконечно-большое число? Пусть мы знаем,
что такое 2; и пусть нам известно, что такое 10. Можем ли мы путем прибавления
отдельных единиц получить из двойки десятку? Конечно, можем. На пути
прибавления к двойке отдельных единиц и лежит то самое число, которое
называется десяткой. Но можем ли мы на этом же самом пути получить
бесконечность? Очевидно, нет. Зная только
одни конечные числа, мы, какими бы арифметическими операциями ни пользовались,
никогда и никак не можем получить бесконечную величину. Это значит, что
бесконечность отличается от конечных величин отнюдь не количественно, а качественно.
Это какое-то особое качество среди количественных операций; и к нему нельзя
прийти путем обычных количественных операций, но только путем «скачка».
Итак, ни
голая процессуальность не определяет бесконечности, хотя и как-то входит в нее,
ни голая количественность не определяет
бесконечности, хотя тоже как-то входит в нее. Приходится, следовательно, искать
иных путей для нахождения понятия бесконечности.
Обратим
внимание на следующее. Бесконечность не увеличивается и не уменьшается от количественного ее увеличения и уменьшения. Стало быть, в каждом отдельном
пункте бесконечность есть уже вся бесконечность, какие бы операции мы над ней
ни производили. Каждый момент
бесконечности есть и вся целая бесконечность. Раз ∞ + А (любое число) =∞, то ясно, что в
бесконечности каждая отдельная ее часть равняется всей бесконечности, взятой в
целом. Этого, разумеется, никогда не бывает в конечной области. Тут всегда
часть меньше целого и целое больше части. Этим область бесконечности коренным
образом отличается от области конечных величин. Тут, однако, кроется и еще одна
категория.
Простое
тождество целого и части еще ничего не говорит о бесконечности, если эти категории брать
самостоятельно. Нужно точнее определить способ отождествления целого и части и
ясно ощущать форму этого отождествления. Этот способ и эта форма не могут быть
статическими. Бесконечность, видели мы, есть прежде всего процесс.
Следовательно, отождествление целого и части должно быть дано в процессе, в
становлении. Становление должно объединить целое и часть или, вообще говоря, целое и дробное, и тут-то и
необходимо искать категорию бесконечности.
Как же
протекает этот процесс отождествления целого и части в бесконечности?
Чтобы
перейти от целого к дробному, надо перейти от бытия к небытию. Дробное—инобытие
целого. Целое, воплотившись в инобытие, превращается в отдельные части и их
сумму. В целом все элементы существенно связаны один с другим, почему они и
являются элементами, или частями. Когда же целое воплощено в инобытии, все его
элементы тоже воплощены в инобытии, но они уже дискретны друг в отношении
друга, так как всякое инобытие есть всегда прежде всего внеположность и
саморазличение, самоотрицание. Итак, целое выражается внешне-инобытийным
образом в дробном, в отдельных частях, в сумме частей, в том, что в отличие от внутреннего центра целости можно
назвать всем. Всё — воплощенное в инобытии целое.
Но если
так, то спрашивается: может ли инобытийная стихия выявить внутреннюю целость
вполне и адекватно? Конечно, может.
Тогда в
инобытии мы находим именно всё. Но
она может выявлять его и не полностью, не адекватно. Становление есть как раз
такая категория, которая мешает в данном случае адекватному выявлению целости.
В целом все дано сразу, а становление все дает постепенно, не сразу.
Следовательно, если дать свободу стихии становления, то целое, хотя и будет все
время дробиться на части (в инобытии) и будет в них постоянно присутствовать,
оно никогда не получит полного выявления и всегда будет только стремиться к
полноте выявления. Целое дробится на части, и эти части призваны выразить его
целиком; но так как части эти тождественны с целым, то количество элементов
целого присутствует в части, она тоже делится на те же части, а часть этой
части опять, в силу своего тождества с целым, содержит в себе то же количество
частей и т. д. и т. д. Идя по этому пути, мы никогда не сможем выразить всего
целого при помощи его частей — и это потому, что части возникают в результате постепенного
дробления, т. е. в результате становящегося дробления, в результате становящегося отождествления целого
и частей.
Теперь
мы можем дать некоторого рода логическую формулу, определяющую понятие
бесконечности.
Бесконечность есть становящееся тождество (или становящийся синтез) целого и дробного.
Это
простейшая концепция бесконечности, без которой невозможно будет понять и
отдельных видов бесконечности. Тут мы видим, что без момента целости нельзя
получить понятие бесконечного. Видим также, что в бесконечность входит и момент
процесса, становления. Необходимо полнейшим образом представлять себе участие
каждого из этих моментов в общем понятии бесконечности.
[…] Бесконечность
не целое и не дробное. Но она и целое, и дробное, и нечто гораздо большее, в
чем обе эти категории как бы взаимно растворяются. Это целое, из объединившее,
есть становление одного другим,
становление целого дробным и дробного, частного—целым. В бесконечности все
последовательные моменты равны один другому, но они в то же время и различны,
так как возникают они в процессе становления. Целое стремится выразиться в
убывающих частях и не может, и части стремятся стать целым и не могут. Все это
в процессе становления по самой природе своей алогично, т. е. нерасчленимо,
неразличимо.
Бесконечность,
таким образом, есть вид становления. От становления вообще
этот вид становления отличается тем, что тут совпадает не просто бытие с
небытием, но именно целое с дробным. Каждый момент бесконечности представляет
собою не просто переход от бытия к небытию и от небытия к бытию, т. е. не
просто уничтожение и возникновение, но переход к раздробленности и обратно, т.
е. рост целостности и дробления. Когда мы движемся в области бесконечности от
одной точки к другой, то тем самым мы, во-первых, удаляемся все в большую
дробность, но в то же время, во-вторых, обнимая все большее и большее
количество точек, мы неизменно стремимся ко все большей и большей цельности.
Такая структура числа, где эти два процесса являются существенно
тождественными, такая структура числа и называется бесконечностью.
Из
предыдущего вполне ясно, что бесконечность
меньше всего определяется размерами. Бесконечность
помещается в любых конечных размерах. Если мы возьмем линию длиною в 5 см,
то на ее протяжении поместится бесконечное количество точек. Если мы возьмем
линию длиною в 1 см, то, очевидно, на ней тоже поместится бесконечное
количество точек. Если мы возьмем линию в 0,1 см, в 0,01 см, в 0,001 см длиною
и т. д. и т. д., то и на этих линиях, как бы малы или велики они ни были, тоже
помещается бесконечное количество точек. Отсюда совершенно ясно: бесконечная величина определяется не
абсолютными размерами числа или вещи, но определенно — взаимоотношением их целости
и их дробности, а именно тем взаимоотношением, когда они даны как полное
тождество. […]
4. Непрерывность (постоянная и переменная величина),
прерывность и предел. Однако прежде чем войти в рассмотрение самого математического анализа, необходимо определить
еще ряд категорий, которые так же
основоположены для анализа, как и понятие бесконечности. Их тоже обычно излагают в случайной форме, не связывая в диалектическую систему, в то время
как это касается самых основных сторон
математики, и они не могут не иметь диалектического строения, если все вообще категории возникают диалектически.
Ряд
категорий, которые требуют нашего рассмотрения, отличаются одним общим
признаком. Число есть непосредственное бытие; в нем нет еще различия между
самим числом и его значением. До сих пор
мы имели число само по себе. Целое,
дробное и бесконечное число есть
значения числа в смысле его внутреннего строения. Чтобы узнать, является ли данное число целым
или дробным, необходимо всмотреться в
само число непосредственно, не обращая никакого специального внимания на фон, его окружающий. Это касается и не только числа. Чтобы судить,
является ли данная вещь цельной, надо,
очевидно, рассмотреть строение самой вещи, как оно дано в контурах, внутри контуров данной вещи. Когда сосуд, напр., имеет трещину или дыру, то для
констатирования этого достаточно только
изучить сосуд в тех границах, которые даны очертанием этого сосуда. И мы вполне будем в состоянии определить, является ли данная ваза целой,
или она разбита. Однако о значении числа
или вещи можно говорить и с точки зрения их внешней судьбы. Можно представить себе, что вещь мыслится совершенно неизменной сама по себе, но что
она погружена или вовлечена в
какое-нибудь изменение, оставаясь сама по себе целой. Можно иметь одно и то же число или комбинацию
чисел и, оставляя их в одном и том же
виде, придавать им те или иные внешние значения. Тут не будет ни просто
числа, взятого в его непосредственности,
вне каких бы то ни было количественных значений, ни числа, в котором имеются в виду только изменения во внутренней структуре. Тут число вступит в
новые значения при полном сохранении
внутренних структур или, вернее, независимо ни от каких внутренних структур.
Прежде
всего величина с этой внешней точки зрения может никак не меняться; она может
иметь, так сказать, нуль изменения. Такую величину называют постоянной величиной. Антитезой к этой
постоянной величине является, очевидно, переменная
величина.
Что
такое постоянная величина и что такое переменная величина, это известно уже из элементарной
математики. В анализе эта пара понятий
играет, однако, гораздо большую роль. […]
Но
интереснее всего то, что получается от соединения этих двух категорий—постоянной и переменной
величин. Диалектический синтез всегда
особенно интересен; он часто таит в себе полную неожиданность. Так, из синтезирования целого и дробного получалась (быть может, с первого взгляда
довольно неожиданно) категория
бесконечности. Что же получится из синтезирования постоянной и переменной величин? Какова та
категория, в которой обе эти категории
совпадают совершенно, точно сливаясь в полную неразличимость на фоне вполне новой и в них не содержащейся конструкции?
Такой
категорией является непрерывность.
Подобно
тому как бытие и небытие объединяются в становление, так и постоянная величина с переменной объединяются в непрерывной величине. […]
Непрерывная величина есть тождество постоянной и
переменной величин.
Непрерывность,
однако, не может быть утверждаема сама по себе, без другой категории, которая с нею соотносительна. Раз мыслится непрерывность, то тем самым должна
мыслиться и прерывность. Одно без
другого совершенно немыслимо. Таким образом, достигнутый нами синтез непрерывности в свою очередь переходит в новый антитезис, в прерывную
величину, и, следовательно, в свою
очередь требует еще нового синтеза.
Синтезом прерывности и непрерывности является предел.
Предел немыслим вне понятия процесса. Предел есть то,
что достигается в течение того или иного определенного процесса. Какой это процесс? Если это есть именно
процесс достижения, то это достижение происходит постоянно, постепенно. Чем больше и дальше двигаемся мы в сфере этого процесса,
тем ближе мы к пределу, тем больше мы
его достигаем. Итак, предел есть некое движение, изменение и некий процесс.
Спросим
теперь себя: какой же именно это процесс? С одной стороны, даже самое понятие предела говорит о
некоей определенности и конечности.
Движение происходит в определенном направлении, и оно имеет какую-нибудь определенную, конечную цель. Без этой идеи не может существовать никакого
предела. Однако, с другой стороны,
предел в математике не мыслится просто, как граница и конец. Этот предел в
математике всегда мыслится как нечто недостижимое, хотя и конечное, как нечто
притягивающее к себе издали приближенную
величину, но никогда не совпадающее с
этой приближенной величиной. Предел, с одной стороны, конечен, а с другой—эта его конечность никогда не
может быть вполне адекватно охвачена.
Как это можно совместить?
Совместить
это можно только тем обычным диалектическим путем, который от бытия и небытия ведет к становлению. Необходимо, чтобы достижение конечного
предела и постоянное его недостижение
совместились во взаимном становлении, т. е. так, чтобы достигнутая конечность все время
сдвигалась с места и заменялась другой,
тоже достигнутой конечностью и чтобы бесконечное, постоянное достижение выражалось, тоже постоянно, в
определенных конечных пунктах. В таком становлении мы получаем, следовательно, бесконечный ряд конечных
величин, но эти конечные величины, уменьшаясь все больше и больше,
приближаются к определенной величине,
хотя никогда ее и не могут достигнуть. […]
Заметим, что становление алогично не
только в том смысле, что оно неразличимо само в себе, само внутри себя, но и в том, что оно
неразличимо и по своей периферии, т. е.
не имеет никаких законченных границ и в этом смысле безгранично. Отсюда понятно, почему становление прерывности непрерывностью или непрерывности
прерывностью никогда не может быть
кончено; по самому смыслу своему оно абсолютно беспрерывно. И значит, предел, диалектически синтезирующий непрерывность и прерывность — по типу
категории становления,— есть в одно и то
же время и полная недостижимость для числового процесса, и выраженность, достигнутость в каждый отдельный момент этого процесса, причем эта
выраженность и достигнутость бесконечно
интенсифицируется, возрастает.
Предел—это
та категория, которая (правда, в довольно вялом виде) применяется уже и в
элементарной математике. Главное ее место, однако, в математическом анализе; и
тут на ней, можно сказать, построена целая наука.
Пусть в
круг вписан квадрат. Если мы удвоим количество его сторон, то площадь его,
конечно, увеличится и периметр его тоже увеличится. Это удвоенное количество сторон может быть удвоено еще раз, еще раз и еще раз. Оно может быть
удвоено до бесконечности. Периметр,
последовательно меняющий свою форму в зависимости от количества удвоений, будет стремиться, очевидно, к окружности и в пределе совпадет с нею. Окружность, говорят, есть предел вписанных многоугольников при
бесконечном увеличении количества
сторон, равно как и предел описанных многоугольников при бесконечном увеличении количества сторон. Здесь окружность есть нечто определенное и
конечное; каждый многоугольник,
вписанный или описанный, с любым количеством сторон, есть тоже величина определенная и конечная; но многоугольник тут дан не сам по себе, но в
своем становлении (в смысле увеличения
количества сторон); потому и количество сторон все время растет, по длине они делаются все меньше, и, значит, в целом же они приближаются все
больше и больше к окружности; окружность
для них—предел. Тут вполне отчетливо выступают две основные категории—непрерывности и прерывности и их синтетическое
взаимопревращение, сплошной и бесконечный переход непрерывности в прерывность и прерывности в непрерывность.
Итак,
вот диалектическая схема указываемых нами понятий: непрерывность, прерывность,
предел, при этом непрерывность сама возникает как синтез постоянной и
переменной величин.
5. Бесконечно-малое и бесконечно-большое. Только
теперь мы можем формулировать то основное понятие, на котором строится весь
математический анализ,— понятие бесконечно-малого (и, значит, бесконечно-большого). Оно возникает
как напряженное, конденсированное
выражение всех только что рассмотренных нами категорий.
Непрерывность
(с постоянной и переменной величинами), прерывность и предел — все это, вместе взятое, может рассматриваться как нечто целое. Именно — это то, что
противостоит числу, взятому в его чисто
арифметическом виде, т. е. числу, взятому как непосредственное бытие. Когда
мы берем числа натурального ряда и производим над ними арифметические действия, то здесь не возникает никаких сопоставлений каждого отдельного
числа с тем или иным его внутренним или
внешним функционированием. Произведя, напр., деление одного числа на другое, мы не ставим никаких вопросов о том, являются ли эти числа,
делимое, делитель и частное, величинами
постоянными, переменными, прерывными, непрерывными или предельными. Никаких таких вопросов тут совершенно не возникает. Это понятно. Все
эти вопросы связаны с числом в том или
ином опосредствованном виде. […]
Самое
простое математическое определение бесконечно-малого есть следующее. Бесконечно-малое есть переменная величина, имеющая своим пределом нуль. С виду
простое, это определение, однако,
содержит в себе немало разных подчиненных моментов, и они враздробь указаны нами в предшествующем,
подготовительном изложении.
Во-первых,
бесконечно-малое есть величина переменная.
Одно уже это тянет за собою всю систему
категорий, которую мы наметили выше. И
уже один этот момент накладывает неизгладимую печать на всю изучаемую нами категорию. Бесконечно-малое—это сплошь стихия
становления, изменения; тут ничто не стоит на месте, все движется и беспокойно требует расширения, углубления, распространения.
Во-вторых,
бесконечно-малое есть такая переменная величина, которая имеет определенный предел. Отнюдь не всякая переменная величина имеет предел, стремится к пределу.
Возьмем самую обыкновенную синусоиду.
Эта равномерно вьющаяся вокруг прямой кривая никуда не стремится, ни к какому пределу не стремится, сколько бы ее ни продолжали. Она проходит
одни и те же значения бесконечное число
раз; эти значения неизменно повторяются, и кривая от этого ровно ни к чему не приближается и не стремится ни к какому пределу. Бесконечно-малое [же] как
раз имеет такой предел, неизменно
стремится к нему; предел управляет бесконечно- малым и притягивает его к себе из таинственного полумрака бесконечности. Это создает для понятия
бесконечно-малого вполне оригинальный
стиль, который еще усиливается от других элементов этого понятия. Подчеркнем, что изменение,
поскольку речь зашла о пределе, дано тут
не само по себе, но в становлении, в алогическом становлении. Оно само стремится в какую-то даль, и стремится сплошно, неразличимо,
безраздельно. Предел, следовательно, достигается тут при помощи бесконечного
процесса приближения. Другими
словами, этот предел никогда и нигде не достигается, а дано только вечное стремление, вечное
движение, неустанный уход в бесконечные
дали.
В-третьих,
бесконечно-малое есть такая переменная величина, которая имеет своим пределом нуль. Нуль в качестве предела рисует всю
нашу картину вечного стремления совсем в другом, в небывалом виде. Что это значит? Что значит
это вечное стремление—и к чему же? К
нулю, в ничто, в небытие! Это значит, что дух, живущий по законам бесконечно-малого, не только стремится куда-то вдаль и не только это
стремление вечно, но, кроме того, тут
ставится задача исчерпания бытия, охвата бытия до последней его точки,
использование его до тех пор, пока не останется в нем нуль бытия, пока не перестанет существовать само бытие и не превратится оно в ничто.
Инфинитезимальный дух хочет исчерпать
все бытие, пережить всю стихию жизни, завоевать до последней точки все существующее, охватить его умом и сердцем, сделать соизмеримым с собою,
адекватным себе, превратить его из
сверхразумной бездны в ощутимую бездну, перевести ее всю-всю целиком на язык своего субъекта,
своего сознания, потопить и растворить в
глубинах собственной личности. Вот что значит это стремление бесконечно-малого к нулю как к своему пределу; и вот почему это не вообще
переменная величина и не вообще процесс,
хотя бы и бесконечный процесс, но процесс, имеющий своею целью нуль, исчерпание охватываемого им бытия до нуля.
В этом
смысле бесконечно-большое мало чем отличается от бесконечно-малого. Если бесконечно-малое есть
переменная величина, стремящаяся к
нулю, то бесконечно-большое, очевидно, есть отношение единицы к этому бесконечно-малому. Если α=1/β, то
при условии lim α=0, lim β=∞, а при
условии lim β=∞, lim α=0. Чем больше
уменьшается α, тем больше увеличивается β; и когда α стремится к нулю, β стремится к
бесконечности. Наоборот, чем больше α, тем меньше β; и когда α стремится к бесконечности,
β стремится к нулю. Тут вполне ясна
связь, существующая между бесконечно- малым и бесконечно-большим. Когда мы имеем какой-нибудь цельный предмет, то, уходя в его глубину с
целью исчерпать его до нуля, пользуясь
идеей бесконечного процесса, мы сразу получаем и бесконечно-малое, и бесконечно-большое: бесконечно-малое мы получаем, если имеем в виду отдельные моменты
процесса, и бесконечно-большое,—если
имеем в виду весь пройденный путь. Если сравнить все целое с отдельной стремящейся точкой, мы получаем уже не просто целое, но целое, разработанное
именно с точки зрения этой отдельной
стремящейся точки, с точки зрения этого бесконечно-малого, т. е. получаем бесконечно-большое. И наоборот, сравнивши бесконечно-большое,
возникшее из всех бесконечно- малых, с
целым, мы замечаем, что оно могло возникнуть действительно только из передвижения бесконечно-малого, т. е.
получаем идею бесконечно-малого. Так
связаны между собой эти оба понятия,
являясь, в сущности, одной и той же идеей, рассматриваемой только с разных точек зрения.
Можно
дать еще другое определение бесконечно-малого, хотя это определение, конечно, в
сущности своей может быть только тождественным с первым. Именно,
бесконечно-малое определяют еще так. Бесконечно-малое есть такая переменная величина, которая может стать меньше любой заданной величины. Пожалуй, это
определение несколько ярче подчеркивает момент процессуальное, играющий такую огромную роль во всем понятии бесконечно-малого. Тут важны именно слова «может
стать меньше любой заданной величины». В них
выражена стихия становления, без которой
бесконечно-малое не существует. В предыдущем определении момент становления и процессуальности выражен слабее,
но зато лучше выражена идея исчерпания
неисчерпания, идея, так сказать, «объятия
необъятного». Этот момент тоже основной в учении
о бесконечно-малом. И таким образом, оба определения, имея в виду один и тот же предмет, подчеркивают в
нем одинаково важные, хотя и различные,
стороны, причем каждая из этих сторон необходимо предполагает другую, так что в конце концов безразлично, какую сторону выдвигать и на
каком определении останавливаться.
Итак,
бесконечно-малое есть диалектический синтез числа в его непосредственном (арифметическом) бытии и
числа в его опосредствованном
(инобытийном в отношении к арифметическому) бытии. Бесконечно-малое есть прежде всего некая
чистая величина, и в этом сказывается
участие здесь арифметического элемента. С другой стороны, это не просто арифметическая
величина со всей ее статической
структурой, но такая величина, которая вобрала в себя и воплотила в себе эти понятия, инобытийные в
сравнении с арифметической статической
раздельностью,— непрерывность, прерывность, предел. Поэтому можно дать такую диалектическую
формулу понятия бесконечно-малого.
Бесконечно-малое есть тождество (синтез)
непосредственно-арифметической значимости числа и
опосредствованно-инобытийного, внутренно-внешнего становления. Этот
момент внутренно-внешнего становления важен потому, что, как мы помним,
бесконечность уже сама по себе,
независимо от ее специального — инфинитезимального, или аналитического, типа
есть синтез целого и дробного, т. е.
синтез внутренних особенностей строения числа, в то время как природа непрерывности, прерывности и предела
возможна у нас на почве именно внешней ориентированности числа на
окружающем его фоне.
Предложенная
формула, конечно, совершенно тождественна с двумя указанными, чисто математическими определениями. Но это есть формула философская, логическая или,
точнее, диалектическая, т. е. основанная на анализе и антиномико-синтетической структуре понятий, в то время как те два
определения суть чисто математические определения, т. е.
основанные на формально-числовом,
формально-счислительном объединении счетных величин. В диалектике — понятия и категории, в математике
— числа и величины. В
диалектике—антиномико-синтетическая связь понятий и категорий, в
математике—счислительно-счетная связь чисел и величин».
Итак, на первый взгляд видимо стоит согласиться с тем,
что бесконечность – это действительно та пучина,
в которой тонет, и не может не пойти на дно, пуская пузыри и в нелепом барахтанье любая формально-рассудочная мысль…
Чтобы плыть, увы, – действительно, как ни странно нужно уметь плавать. В самом худшем
случае и как говорится на худой теоретический
конец – хотя бы понимать, что стихия, которой ты в данный момент окружен,
предполагает совершенно иные двигательные движения рук и ног, которые очень существенно
отличаются от указанных движений по поверхности земли в газовой среде.
Впрочем, возможно, конечно же, и прямо противоположное,
но, по сути, также подпадающее под описываемую концепцию прохудившегося до
неприличия ментального «конца»: совершенно неразумно нырять в бассейн, в
котором полностью отсутствуют условия для реализации плавательных движений, или
попросту говоря, в котором нет воды…
Для того человечеству и дан весьма длительный и
непростой период адаптации, являющийся временем различения и выявления форм и
типовых отношений в этих формах и к этим формам, чтобы наконец, быть готовым к
любым поворотам судьбы; которой то ли
к счастью, то ли к несчастью, то ли к непостижимому человечьим умом единству этих
двух – не существует.
Нет судьбы, есть Провидение, надо лишь
видеть его.
Но чтобы видеть Его необходимо видеть Им.
Последнему, впрочем, научить и вовсе невозможно, а научиться не так легко, как может, и вдруг захочется легионам ныне беззаботно и в весьма
специфической радости беснующихся слепцов.
Но, кажется, пора двигаться вперёд, пора отчалив навсегда от чужих формально-конечных математических берегов, беззвучно скользить
над бездной пучины-в-которой-тонет-всё, стараясь не вспенить её волнующейся поверхности,
скрывающей бесконечно прозрачную хрустальную тайну того, что не имеет границ:
Прощай, чужая
земля,
Но нам здесь
больше нельзя.
Мы стали легче
тумана,
Мы стали чище
дождя.
Мы вновь вернемся
сюда,
Но кто нам
скажет тогда:
"Прощай, чужая
земля,
Прощай!"
«На протяжении последних
десятилетий математика прямо-таки упивалась всякого рода обобщениями и
формализациями. Однако считать, будто она стремится к общему ради общего,
значит неверно понимать заключенную здесь здоровую тенденцию. Дело обстоит
иначе: любое естественное обобщение упрощает, сокращая допущения, и тем самым позволяет понять определенные стороны
некоторого необозримого целого. Разумеется, вполне может случиться, что
обобщения в различных направлениях принесут понимание конкретного положения
вещей в различных аспектах. В этом случае разговор
об истинной основе, истинном источнике этого положения вещей отягчен
субъективным и догматическим произволом»
Это - Герман
Вейль, пожалуй, наиболее последовательный мыслитель-и-математик 20-го столетия,
последовательный в правильной, т.е. соответствующей Истине постановке вопроса
оснований математики и направления её развития, и на своём пути не раз
достигавший выдающихся прозрений:
«Математика — это наука о бесконечном. Великим достижением
греков было преобразование полярной
противоположности конечного и бесконечного в мощное и плодотворное орудие
познания действительности. Интуиция бесконечного, спокойное и не задающееся
никакими вопросами признание его были присущи восточному миру. Но на востоке
эта интуиция оставалась лишь чисто абстрактным сознанием, равнодушно
оставлявшим существование рядом с собой неоформленного, необработанного
конкретного многообразия вещей. Это пришедшее с востока религиозное чувство
бесконечного
 овладело греческой душой в предшествовавшую
греко-персидским войнам дионисо-орфическую эпоху. Греко-персидские войны и в
этом отношении знаменовали собой разрыв западного мира с восточным. С этого
момента указанная полярность и стремление к ее преодолению стали для греков
движущим мотивом познания. Но всякий раз, когда, казалось, уже удавалось
достигнуть желанного синтеза, старое противоречие возникало вновь и притом в
еще более углубленном виде. Противоречие это определяло собою вплоть до наших
дней ход развития теоретического познания.
овладело греческой душой в предшествовавшую
греко-персидским войнам дионисо-орфическую эпоху. Греко-персидские войны и в
этом отношении знаменовали собой разрыв западного мира с восточным. С этого
момента указанная полярность и стремление к ее преодолению стали для греков
движущим мотивом познания. Но всякий раз, когда, казалось, уже удавалось
достигнуть желанного синтеза, старое противоречие возникало вновь и притом в
еще более углубленном виде. Противоречие это определяло собою вплоть до наших
дней ход развития теоретического познания.
Тот вид, в котором понятие бесконечности
могло быть введено в науку, впервые ему придан был Анаксагором. В одном
дошедшем до нас отрывке из его сочинений говорится: «В малом не существует
наименьшего, но всегда имеется еще меньшее. Ибо то, что существует, не может
исчезнуть, как бы далеко ни было продолжено деление". Речь здесь идет о
пространстве или о теле; непрерывное, говорит Анаксагор, не может состоять из
дискретных элементов, которые отделены друг от друга и как бы отрублены друг от
друга ударами топора. Пространство бесконечно не только в том
смысле, что в нем не имеется конца; оно кроме того в любом своем месте
бесконечно, так сказать, во-внутрь, и точка в нем может быть определена лишь
путем бесконечного и от раза к разу все точнее и точнее фиксирующего ее
процесса деления. Это представление противоречит интуиции покоящегося и
законченного в себе бытия пространства. Для заполняющего его
многообразия качеств пространство служит принципом их разграничения, впервые
вообще создающим возможность существования различия в сфере качественного;
однако пространство является не только принципом разграничения, но вместе с тем
и принципом соприкосновения, непрерывной связи, в силу которой ни одна вещь не
может быть отрублена от другой „как бы ударами топора". […]
Исчисление бесконечно малых нового времени, преобразованное Лейбницем и
Ньютоном в мощное орудие для изучения природы, не могло со стороны логической
своей строгости итти в сравнение с греческой теорией континуума. Зато
значительно обширнее оказалась ныне область подлежащих его ведению проблем.
Теперь речь стала итти уже об исследовании любых непрерывных форм и процессов,
в особенности, же процессов движения. Страстная воля к действительности превалирует в эпоху нашей культуры
над прозорливым греческим ratio. Если в свое время Эвдокс в строго
сформулированной аксиоме отбросил понятие бесконечно малого, то теперь как раз
наоборот, именно это расплывчатое и полное непостижимой загадочности представление
положено было в основание нового исчисления *). Правда основоположники его Ньютон и Лейбниц довольно ясно выразили ту
правильную идею, что речь идет не о законченном бесконечно малом, а о
предельном переходе к нулю, но эта точка зрения не являлась первенствующей в
общем ходе их мыслей, и они, очевидно, не знали, что выполнение перехода к
пределу не только требует определения значения предела, но обязано также в
первую очередь гарантировать его существование. По отношению к Ньютону дело
объясняется тем, что в случае движения конкретный процесс его заключает в себе,
по мнению Ньютона, в качестве момента скорость до всякого математического
анализа. Что касается Лейбница, то взгляды его были затемнены тем ложным
метафизическим представлением, будто бесконечно малое должно иметь место не в
качестве чего-то действительно существующего, а только как чисто логическое
основание.
И среди преемников Ньютона и
Лейбница господствовал в общем тот взгляд, что бесконечно малые величины,
бесконечно близкие точки на кривых и т. п. действительно существуют. С
бесконечными рядами оперировали, не обращая внимания на вопрос об их
сходимости. И хотя при этом все-таки ощущались некоторые затруднения и то в
одном, то в другом пункте возникали неразрешимые противоречия, но что все это означало
по сравнению с грандиозными успехами анализа и базирующегося на нем
математического естествознания: „Allez en avant et la foivous viendra" *). Лишь крайне медленно развилась
более осторожная теория пределов; только в начале XIX в. Коши удалось
последовательное проведение ее и растворение застывшего бытия бесконечно малых
величин в процессе перехода к пределу.
В новейших аксиоматических
изысканиях в области арифметики и геометрии были построены разнообразные
числовые системы, в которых аксиома Эвдокса не выполнена. Таким образом совсем
не невозможно выработать такую четкую и свободную от противоречий систему
арифметики, в которой имелись бы величины различных порядков. Но вместе с тем очевидно, что подобная
арифметика была бы совершенно непригодна для анализа, ибо суть исчисления
бесконечно малых заключается ведь в том, что на основании подчиненных известным
элементарным законам отношений в области бесконечно малых величин познают при
помощи интегрирования отношения, существующие в области величин конечных. Если
же мы станем в анализе рассматривать бесконечно малые не с точки зрения
процесса перехода к пределу, то процессы в области конечного и бесконечно
малого становятся тогда совершенно чуждыми, независимыми друг от друга, и
связующая их цепь оказывается разомкнутой. Взгляды Эвдокса в данном вопросе
были несомненно правильными».
К слову, Вейль в своём докладе-выступлении, который дополняет
приведенный выше опорный материал (в
который мы будем далее вникать и учиться его
понимать) и называется «Математический способ
мышления» поднимает и иные весьма
важные для нас в текущий момент вопросы, в частности вопрос почему мы,
например, рассматривая реализацию моделей, поясняющих и главное – показывающих диалектические отношения форм, говорим именно о топологии:
«…Мы умышленно избрали
топологический подход, поскольку только он позволяет достичь широты,
достаточной для того, чтобы мы могли охватить одновременно специальную и общую
теорию относительности. Специальная теория относительности рассматривает
причинную структуру как нечто геометрическое, жесткое, заданное раз и навсегда,
в общей же теории относительности эта структура обретает гибкость и зависимость
от вещества - так же, как, например, электромагнитное поле.
Анализируя природу, мы расчленяем
явления на простые элементы, каждый из которых изменяется в определенном
диапазоне возможностей, диапазоне, который обозрим для нас apriori потому, что
эти возможности мы строим apriori чисто комбинаторным образом из некоего чисто
знаковою материала. Многообразие точек пространства-времени является одним из
конструктивных элементов природы, по-видимому, наиболее важным. […]
До сих пор я всячески подчеркивал
конструктивный характер математики. В нашей фактически существующей математике
с ним соперничает неконструктивный аксиоматический метод. Его
классическим прототипом являются аксиомы геометрии Евклида. Аксиоматический
метод был весьма остроумно использован Архимедом, а впоследствии Галилеем и Гюйгенсом
при создании науки механики. При аксиоматическом методе все понятия
определяются через несколько неопределяемых основных утверждений — аксиом,
относящихся к основным понятиям. В прежние времена создатели теорий были
склонны утверждать априорную очевидность своих аксиом, но это
эпистемологический аспект проблемы, не представляющий интереса для математика. Дедукция
происходит в соответствии с принципами формальной логики, в частности, следует
схеме силлогистического вывода. Подобное аксиоматическое изложение
moregeometrico на протяжении долгого времени считалось идеалом любой науки. Спиноза предпринял попытку применить его к
этике. Для математика безразличен смысл слов, выражающих основные понятия;
любая их подходящая интерпретация, т.е. такая, при которой аксиомы становятся
истинами, одинаково пригодна, и все суждения аксиоматизируемой дисциплины при
такой интерпретации сохраняют свою силу, поскольку все они являются логическими
следствиями из аксиом. […]
… математика рассматривает
отношения в гипотетически-дедуктивном плане, не связывая себя никакой
конкретной материальной интерпретацией. Ее
интересует не истинность аксиом, а лишь их непротиворечивость; в
самом деле, противоречивость apriori лишала бы нас надежды когда-нибудь найти
подходящую интерпретацию. […]
Все же я считаю своим долгом
заметить, что с тех пор, как аксиоматический подход перестал быть излюбленной
темой специалистов по методологии, его влияние распространилось с корней на все
ветви математического древа. Как мы уже успели убедиться, в основе топологии
должен лежать полный перечень аксиом, определяющих топологическую схему. Одним из простейших и наиболее фундаментальных понятий, задаваемых
аксиоматически, может служить понятие группы, проникшее во все разделы
математики. Алгебра с ее полями, кольцами и т.п. от вершины до основания
пронизана аксиоматическим духом. […]
Рассмотри сначала первую
альтернативу. Приняв ее, мы должны считать, что математика есть прежде всего
конструкция. Используемые в математике системы аксиом лишь устанавливают
границы области значений тех переменных, которые участвуют в конструкции. Поясню это утверждение несколько подробнее на наших примерах причинной
структуры и топологии. Согласно специальной теории относительности причинная
структура задана раз и навсегда и поэтому может быть построена явно. Более
того, эту структуру разумно строить вместе с соответствующей топологической
средой, подобно тому, как, например, окружность вместе со своей метрической
структурой получается путем выполнении нормального разбиения — деления каждой
дуги на две равные части. Однако в общей теории относительности
причинная структура представляет собой нечто гибкое: она должна лишь
удовлетворять некоторым аксиомам, выведенным из опыта и оставляющим достаточную
свободу. Но по мере развития теории устанавливаются законы природы, связывающие
гибкую причинную структуру с другими гибкими физическими сущностями —
распределением масс, электромагнитным полем и т. д., и эти законы, в
которых гибкие явления выступают как переменные, в свою очередь оказываются
результатом явных априорных теоретических построений. […]
Но довольно о первой альтернативе.
Если принять противоположную точку зрения, то конструкция оказывается
подчиненной аксиомам и дедукции, математика же предстает в виде системы аксиом,
выбор которых зависит от соглашения, и выводимых из них заключений. В полностью
аксиоматизированной математике конструкции отводится второстепенная роль: к ней
прибегают при построении примеров, образующих мост между чистой теорией и ее
приложениями. Иногда существует лишь один пример, потому что аксиомы
определяют некий объект однозначно или по крайней мере с точностью до
изоморфизмов; в этом случае необходимость перехода от аксиоматической структуры
к некоторой явной конструкции становится особенно настоятельной. Еще более существенно отметить, что хотя
аксиоматическая система и не предполагает построения математических объектов, она, комбинируя и неоднократно используя логические правила, строит
математические суждения. Действительно, извлечение следствий из заданных
посылок происходит по определенным логическим правилам, которые со времен
Аристотеля неоднократно пытались свести в единый полный перечень. Таким
образом, на уровне суждений аксиоматический метод есть чистейшей воды
конструктивизм. В наши дни Давид Гильберт довел аксиоматический метод до
горького конца, когда суждения математики, включая аксиомы, превратились в
формулы и игра в дедукцию свелась к выводу из аксиом тех или иных формул но
правилам, не учитывающим смысла формул. Игра в математику происходит в полном
безмолвии, без единого слова, как игра в шахматы. Слова нужны лишь для того,
чтобы объяснить и сообщить «игрокам» правила; и, разумеется, все рассуждения о
возможностях игры, например выяснение вопроса о ее непротиворечивости, также происходит
в среде слов и апеллирует к данным опыта.
На этом этапе, коль скоро он достигнут, расхождение между явной
конструкцией и неявным аксиоматическим определением затрагивает самые основы
математики. Конструктивный
опыт перестает подкреплять принципы аристотелевской логики, когда эти принципы
применяются к экзистенциальным или общим суждениям, относящимся к бесконечным
областям, таким, как последовательность целых чисел или континуум точек. Если
же мы примем во внимание логику бесконечного, то нам вряд ли удастся адекватно
аксиоматизировать даже самые примитивные процессы, например, переход n1 -> n2, т. е. от целого числа n к следующему числу n'. Как
показал К. Гёдель, всегда найдутся конструктивно очевидные арифметические
суждения, не выводимые из аксиом, как бы вы их ни формулировали, и в то же
время аксиомы, безраздельно правящие всеми тонкостями конструктивной
бесконечности, выходят далеко за пределы того, что может быть подтверждено
опытом. Нас не удивляет, что фрагмент природы, взятый в своем феноменальном
изолированном бытии, бросает вызов нашему анализу с его незавершенностью и
неполнотой; именно ради
полноты, как мы видели, физика проецирует то, что дано, на то, что могло бы
быть. Но удивительно другое: конструкция, порожденная разумом, — последовательность
целых чисел, эта простейшая и самая прозрачная для конструктивного ума вещь, —
обретает аналогичную неясность и ущербность, если подходить к ней с позиций
аксиоматики. Но тем не
менее это факт, отбрасывающий зыбкий отблеск на взаимосвязь опыта и математики.
Несмотря на проницательность критической мысли — а может быть, благодаря ей —
мы теперь гораздо меньше, чем наши предшественники, уверены в тех глубинных
устоях, на которых покоится математика».
Мы начнём, конечно, с непоколебимой
уверенности, уверенности в глубинных устоях, на которых по словам Вейля должна
покоится математика, чтобы стать собой – уверенностью, должна стать простым знанием опять же простого понимания этих
устоев:
А) Единство
субъекта и объекта мышления, единство, порождающее бесконечное, конечное и их непрерывный
переход друг в друга через самих себя:
«Когда мы говорим о мышлении, мы должны различать между конечным, лишь
рассудочным мышлением, и бесконечным, разумным мышлением. Определения мышления,
которые мы непосредственно преднаходим изолированными, суть конечные
определения. Истинное же есть в себе бесконечное, которое не может быть
выражено и осознано посредством конечного. Выражение
бесконечное мышление может казаться странным, если придерживаться представления
новейшего времени, будто мышление всегда ограничено. На самом деле, однако,
мышление по своей сущности в себе бесконечно. Конечным называется, выражаясь
формально, то, что имеет конец, то, что есть, но перестает быть там, где оно
соприкасается со своим другим и, следовательно, ограничено последним. Конечное,
таким образом, состоит в отношении к своему другому, которое является его
отрицанием и представляет собой его границу. Но мышление находится у самого
себя, соотносится с самим собой и имеет своим предметом само себя. Делая мысль
своим предметом, я нахожусь у самого себя. «Я», мышление, согласно этому,
бесконечно, потому что оно в мышлении соотносится с предметом, который есть оно
само. Предмет вообще есть нечто другое, нечто отрицательное по отношению ко мне.
Но если мышление мыслит само себя, то оно имеет предмет, который вместе с тем
не есть предмет, т. е. имеет снятый, идеальный (ideeller) предмет; мышление как
таковое в своей чистоте не имеет, следовательно, предела в себе. Конечным оно является лишь постольку,
поскольку оно останавливается на ограниченных определениях, которые признаются
им чем-то последним. Бесконечное,
или спекулятивное, мышление точно так же определяет, но, определяя,
ограничивая, оно снова снимает этот недостаток. Не следует подобно обычному
представлению понимать бесконечность как абстрактное выхождение за всякий вновь
возникающий предел, а следует понимать его тем простым способом, который мы
разъяснили выше».
«Абсолютное знание
есть истина всех способов сознания, потому что, как показало [описанное в
"Феноменологии духа"] движение сознания, лишь в абсолютном знании
полностью преодолевается разрыв между предметом и достоверностью самого себя, а
истина стала равной этой достоверности, так же как и эта достоверность стала
равной истине.
Чистая наука, стало
быть, предполагает освобождение от противоположности сознания [и его предмета].
Она содержит в себе мысль, поскольку мысль есть также и суть вещи (Sache) сама
по себе, или содержит суть вещи саму по себе (die Sache an sich selbst),
поскольку суть вещи есть также и чистая мысль. В качестве науки истина есть
чистое развивающееся самосознание и имеет образ самости [что выражается в том],
что в себе и для себя сущее есть осознанное (gewusster) понятие, а понятие, как
таковое, есть в себе и для себе сущее. Это
объективное мышление и есть содержание чистой науки. Она поэтому в такой мере
не формальна, в такой мере не лишена материи для действительного и истинного
познания, что скорее лишь ее содержание и есть абсолютно истинное или (если еще
угодно пользоваться словом "материя") подлинная материя, но такая
материя, для которой форма не есть нечто внешнее, так как эта материя есть
скорее чистая мысль и, следовательно, есть сама абсолютная форма. Логику, стало
быть, следует понимать как систему чистого разума, как царство чистой мысли.
Это царство есть истина, какова она без покровов, в себе и для себя самой.
Можно поэтому выразиться так: это содержание есть изображение Бога, каков он в
своей вечной сущности до сотворения природы и конечного духа».
Б) Метафизическое мышление было мышлением конечным, причина этого –
застывший формализм понимания «предельного» как чего-то такого, что не может быть отрицаемым. Но любой предельный переход потому способен
охватить предельное – само себя – и
выйти за его-свои границы, что эти границы находятся не извне, а в самих
глубинах того что понимается неким предельным и бесконечным:
«Мышление прежней метафизики было конечным мышлением, ибо она двигалась
в таких определениях мышления, предел которых признавался ею чем-то незыблемым,
не могущим в свою очередь подвергнуться отрицанию».
В)
Важнейшим является правильное понимание понятия именно как «понятие понятия»,
которое является особенным движением, а именно движением саморефлексии или
самодвижением понятия в самом себе; такое движение приводит к тому, что постигая
понятие человеческий разум раздваивается в нём – в себе – но улавливая движения
раздваивания он в самом движении раздваивания-противоположения видит движение
соединения раздвоенного. Причине этого в том, что каждая противоположность
содержит в самом себе определение своего противоположного, а единство
противоположностей является выражение сущности понятия:
«Отсюда для понятия сразу же вытекает следующее более точное
определение. Так как в-себе-и-для-себя-бытие непосредственно дано как положенность, то понятие в своем простом
соотношении с самим собой есть абсолютная определенность, которая, однако, как соотносящаяся лишь с собой есть точно так же
непосредственно простое тождество. Но это соотношение определенности
с самой собой как ее слияние (Zusammengehen) с собой есть также отрицание
определенности, и понятие как это равенство с самим собой есть всеобщее. Но это
тождество имеет точно так же и определение отрицательности: оно отрицание, или определенность,
которая соотносится с собой; как такое, понятие есть единичное. Каждое из них
есть тотальность, каждое содержит внутри себя определение другого, и потому эти
тотальности суть в такой же мере просто лишь одна тотальность, в какой это
единство есть расщепление самого себя, превращение себя в свободную видимость
этой раздвоенности, раздвоенности, выступающей в различии между единичным и
всеобщим как полная противоположность, которая, однако, настолько есть
видимость, что
когда постигается и высказывается одно, при этом непосредственно постигается
и высказывается другое.
Только что изложенное следует
рассматривать как понятие понятия. Может показаться, что это понятие не согласуется с тем, что обычно понимают под
понятием, и можно было бы потребовать, чтобы было указано, каким образом то,
что здесь оказалось понятием, содержится в других представлениях или
объяснениях. Однако, с одной стороны, здесь не может идти речь о подтверждении,
основанном на авторитете обыденного
понимания; в науке о понятии его содержание и определение может быть
подтверждено только посредством имманентной
дедукции, содержащей его генезис, и эта дедукция уже находится позади нас. С другой стороны, дедуцированное здесь понятие необходимо распознать в том самом, что
обычно предлагается как понятие понятия. Но не так-то легко выяснить
то, что другие говорили о природе понятия. Ведь большей частью они вовсе не
занимаются отыскиванием этой природы и предполагают, что когда говорят о
понятии, каждому уже само собой понятно, о чем идет речь».
Г) Развитие и воплощение Всеобщей Мысли в сфере абстрактно-математического познания
по существу так и не смогло достигнуть высшего и необходимого уровня и
основания – уровня и основания спекулятивного гегелевского мышления его
философской системы, застряв в общем и целом на первой ступени, на И.Канте и на
его «вещи-в-себе». Бесконечное у
Канта осталось содержательно формальным. Но форма не только может быть выражением и средством
постижения истинного скрытого под
ней, но и должна ей быть, ибо мысль двигаясь к основе основ не просто сводит эту
основу к бесконечности ничто, но видит это «ничто» само формой бесконечного
бытия. Понятие, утверждает Ф.Гегель есть
форма абсолютного, которая выше бытия
и сущности, абсолютное является абсолютным основанием и являясь им определяет
любую форму как абсолютную, рождающуюся в результате соотнесения абсолютного с
самим собой. Форма, явление, таким образом, позволяют не только двигаться
к абсолютной истине, но и достигнуть её.
Пустая непостижимая и потому бессмысленно-бессодержательная форма в виде «вещи-в-себе» раскрывается, и раскрывается именно
для себя, и для себя не как исключительно «сотворенного» и потому
поднимающегося лишь до уровня «вещности», но равноправного со-творца:
«Так как Кант определяет отношение разума к категориям как лишь диалектическое и притом понимает
результат этой диалектики просто как бесконечное
ничто, то бесконечное единство разума утрачивает еще и синтез, а тем самым
и упомянутое выше начало спекулятивного, истинно бесконечного понятия; оно
становится известным, совершенно формальным, чисто регулятивным единством систематического применения рассудка. Кант
считает злоупотреблением со стороны логики то, что логика, которая должна быть
только каноном критической оценки, рассматривается как органон для
образования объективных взглядов.
Понятия разума, в которых следовало бы ожидать более высокой силы и более
глубокого содержания, уже не имеют ничего конститутивного, как это еще имело место у категорий; они только идеи; их, правда, вполне дозволительно применять, но под этими умопостигаемыми сущностями, в которых должна была
раскрываться вся истина, разумеют не
что иное, как гипотезы, приписывать
которым истину в себе и для себя было бы полным произволом и безумной
дерзостью, так как они не могут
встретиться ни в каком опыте. - Можно ли было когда-нибудь подумать, что
философия станет отрицать истину умопостигаемых сущностей потому, что они
лишены пространственной и временной материи чувственности?
С этим непосредственно связана точка зрения, с которой следует вообще
рассматривать понятие и назначение логики и которая в философии Канта
понимается так же, как это обычно принято, а именно отношение понятия и науки о
нем к самой истине. Уже выше было
сказано о кантовской дедукции категорий, что, согласно ей, объект, в котором объединяется многообразное, охватываемое созерцанием, есть это единство лишь через единство самосознания. Здесь,
следовательно, определенно говорится об объективности
мышления, о тождестве понятия и вещи, которое и есть истина. Подобным образом и вообще признается, что, когда мышление
усваивает данный предмет, это предмет тем самым претерпевает изменение и
превращается из чувственного в мыслимый, но что это изменение не только ничего
существенного в нем не изменяет, а, напротив, он истинен именно в своем понятии; в непосредственности же, в которой
он дан, он лишь явление и случайность; что познание предмета,
постигающее его в понятии, есть
познание его таким, каков он в себе и для
себя, и что понятие и есть сама его объективность. Однако, с другой
стороны, опять-таки точно так же утверждается, что мы все же не можем познавать вещей, каковы они в себе и для себя, и
что истина недоступна познающему разуму; что та истина, которая состоит в единстве объекта и понятия, есть все же лишь
явление и притом опять-таки потому, что содержание-де есть лишь то
многообразное, что дано в созерцании. По этому поводу было уже отмечено, что,
напротив, именно в понятии снимается это многообразие, поскольку оно
принадлежит созерцанию в противоположность понятию, и что через понятие предмет
возвращают к его неслучайной существенности; эта существенность выступает в
явлении, и именно поэтому явление есть не просто нечто лишенное сущности
(Wesenloses), а проявление (Manifestation) сущности. Но ставшее вполне свободным проявление сущности и есть понятие. - Это
не значит, что положения, о которых мы здесь напоминаем, суть догматические
утверждения, ибо они выводы, вытекающие сами собой из всего изложения сущности.
Теперешняя точка зрения, к которой привело это изложение, состоит в том, что понятие есть форма абсолютного, которая выше
бытия и сущности».
Итак, логика диалектической логики
не так уж сложна, но необходимо уметь, как говорит Ф.Гегель возвыситься от созерцания
и представления о предмете до понятия и мысли о нём, мысли, которая охватывает своё охватывание предмета, но
такое охватывание вовсе не следует понимать как абстрактное выхождение за вновь
возникающий предел, от чего предостерегал Ф.Гегель:
«Не следует подобно обычному
представлению понимать бесконечность как абстрактное выхождение за всякий вновь
возникающий предел, а следует понимать его тем простым способом, который мы
разъяснили выше».
Речь здесь о том, что:
«…мышление по своей сущности в себе бесконечно. …
Конечное… состоит в отношении к своему другому, которое является его отрицанием
и представляет собой его границу. Но мышление находится у самого себя,
соотносится с самим собой и имеет своим предметом само себя. Делая мысль своим
предметом, я нахожусь у самого себя. «Я», мышление, согласно этому, бесконечно,
потому что оно в мышлении соотносится с предметом, который есть оно само».
И необходимо особо отметить, что именно это особое движение – движение рефлексии, находится в основании всех пока что непознанных
или непонятых тайн в философии, логике, геометрии и математике, физике, социологии
и политике…
Итак, мысль, настоящая мысль именно как особое движение себя – в себе самой и
далее все иные уже отмеченные аспекты рефлексивного движения, осуществляется автоматически, а точнее – естественно и в соответствии с природой самой живой человеческой мыслеформы которая научилась порождать саму себя и тем самым отныне способна стать и быть живой.
Именно отныне мысль – это живая мысль, самодействующая мысль в
которой движение мысли неотличимо от движения мышления и оба
движения едины как сознание осознающее себя.
Сознание – в общем конечно,
ибо сознанием обладают не только люди, но и животные.
Но рефлексия
сознания раскрывает конечное и выводит его за границы самого себя и делает тем
и таким кем и каким оно есть в своей действительности – бесконечной и всеобщей
рефлексией осознания.
Всеобщее (т.е. «Всеобщее
Сознание») как развивающаяся Единая-Живая-Совокупность всех
форм воплощенных сознаний начало осознавать себя или иными словами,
стало научно отражать отражение своего понимания целым рядом своих
выразителей-мыслителей известных ныне человечеству как блестящая плеяда
известнейших и гениальных ученых финала восемнадцатого,
всего девятнадцатого и начала двадцатого столетия.
Ведущая особенность описываемого этапа – его
рефлексивность.
Сознание – Всеобщее – осознаёт, осознаёт себя и осознаёт себя сознающим – т.е. является таким,
что достигло качественно нового уровня способности мыслить само себя в самых
различных сферах своей активности.
Для нас же интересными и важнейшими являются сферы
философии, математики (в некоторой мере физики) и социологии, как областей
требующих наибольшей меры абстрагирования как формы построения живой
развивающейся фрактальной структуры осознания предмета сознания.
Философия Ф.Гегеля является наиболее чистой философской формой рефлексивного
инварианта Всеобщего Движения Сознания за указанный период.
Выделяя важнейшее отличие этой философии от всех иных
можно сказать, что это первая истинная философия, это рождение Науки Абсолютного
Основания.
Именно к указанного рода основанию, хотя и дольно противоречиво,
двигалась и математика рассматриваемого нами периода.
Итак, абстрактно-математической формой того же Движения Всеобщего именно как движения
становления Абсолютного Основания являются:
- теория бесконечно малых и понятия
дифференциала, интеграла и производной;
- теория математического предела;
- теория
бесконечных множеств Г.Кантора;
- теория
комплексных чисел;
- неевклидова и проективная
геометрия.
Наша задача в данной Главе наглядно это, окантовав,
таким образом, и этим окончательно утвердив
законность и необходимость философии Ф.Гегеля как особой рефлексивной формы
именно научного мышления.
Именно
истинное научное мышление как мышление
абсолютного основания должно и призвано изменить мир людей, а вера, чудеса и
религиозность как и мифы о «втором пришествии» были необходимы для предыдущей
фазы развития человечества.
Гегелевская
философская система является той единой и единственной Интеллектуально-Духовной
Почвой, в которой взрастут Зерна грядущего Одухотворенного Единого Мира, напряженно
ожидающего воистину исторического момента вырваться из оков грубой
материальности и открыть пред собой Беспредельность Духовных Небес.
Этот Мир, Мир в
котором будет господствовать Дух Всеобщего и Цвести и Плодоносить Истинное
Единство Всех в Истине вызревал на протяжении более чем двух столетий, и
первая попытка его воплощения в мире и её судьба всем нам хорошо известна.
Но Всеобщее – Существует. Всеобщее – Мыслит. Всеобщее
– Действует.
В соответствии со Своей Волей.
Воля Всеобщего выступает и проявляется перед Своим-Иным
– сознаниями своего особенного и единичного как Закон.
Большинство, а
точнее абсолютное большинство не в
состоянии ни постичь эту Волю, ни даже само Её существование, как не в
состоянии увидеть в хаосе сменяющих друг друга форм неуклонность поступательного
действия Закона и Воли.
В действительности, то есть под
поверхностью форм явлений, сменяющих друг друга в непонятной игре – в необходимом
основании себя, в общем и всеобщем движении, моменты и проекции которого они
составляют, эта Воля и Закон не просто просты и незамысловаты, но скорее даже до неприкрытого неприличия просты и
являются уже знакомым нам Вечным Становлением, Законом Единства, законом
перехода противоположностей друг в друга.
Итак,
Всеобщая Воля выглядит на нашем плане в лучшем случае немыслимо распыленной и лишь иногда концентрируется – выявляясь – в воле тех немногих, кто оказывался, как принято говорить «волей судеб», а
в действительности просто Волей Всеобщего во главе миллионов, движение которых
становится движением Истории. Но даже те, кто становится во главе таких течений,
как правило, не в состоянии постичь творимого собой и не понимает, почему происходит
то, что происходит.
К слову, трудно сказать в каком смысле эту волю можно назвать «Божьей Волей», ибо указанный
термин глубоко и, пожалуй, непоправимо формален гнилостью тупоумия религиозной догматики,
которая отрывает т.н. «Бога» от т.н. «человека», совершенно не понимая
порождающей связи и глубинного единства обоих, и этим действием совершающего,
пожалуй, смертный грех всех смертных грехов.
Человек – не
может быть без Бога.
Но и Бог не
может быть без человека. Одно
предполагает другое и существует в другом и переходит, движется к нему по
спирали, спускаясь к неведомому и существующему лишь в Мифах центру-фокусу, в
котором Бог неотличим от человека, а человек – от оживляющей его Всеобщей Воли.
Итак, Всеобщее («Бог») Мыслит, и эти Мысли, а точнее,
разумеется, их формы и есть суть события материального, наблюдаемого и
отчасти понимаемого человеком мира.
И трудно это отрицать в принципе, ибо Всеобщая Мысль так или иначе практически явлена своими многочисленными, почти неисчислимыми человеческими
проекциями мысли, каждая из которых несет на себе свой удивительный и
неповторимый отпечаток, свою печать
подлинности, и наверное несёт в себе и Истину, хотя несёт её в уникальной форме и является истиной как
правило где-то почти невыявляемо глубоко в
себе.
Крайне редко лишь в переломный моменты Истории Всеобщее явлено
открыто, явно, недвусмысленно и осмысленно в самой человеческой
форме и так Всеобщая мысль соединяется со своим-иным, со своим единичным-человеческим – с какой-то конкретной личностью и мыслится этой личностью одновременно,
параллельно-синхронно с Всеобщим, ибо и опирается и исходит из основы
основ.
Рассматриваемый перелом в сознании человечества начал
осуществляться на рубеже веков – 18-го и 19-го.
Можно утверждать, что вот уже более двух столетий впервые человечество как целое учится мыслить и учится понимать помысленное собой.
Именно это и является предметом нашего рассмотрения в Пятой Главе в отношении
самой абстрактной и потому очень близкой к Всеобщему Формы.
Кроме того необходимо учесть, что Пятая Глава завершает
Первую Часть Книги, в которой мы совместными усилиями учились мыслить и понимать, учились
мыслить мышление понимания и понимать
и видеть мысли – свои и мысли других людей.
Завершение любого рода требует известного подведения
итога. Ведь путь проделан немалый. И потому мы для продолжения пути оглянем то,
что пройдено и подумаем над пройденным, и попробуем увидеть подуманное, ведь именно в этом цель наша.
По сути дела вся Первая Часть Книги является весьма
многословным и очень подробным пояснением, разъяснением и выяснением того, что означает загадочные слова мантры гегелевского философского заклинания
способного расколоть… нет, скорее – превратить в пыль одну на всех скалу тотальности
непонимания всеми – всех, в
которую вмурована истинная, потому что Единая Человеческая Свобода: «противоположности
переходят друг в друга через самих себя, через то, что они есть».
Эти слова наиболее простая и доступная пониманию формула выражения Всеобщего Закона, воистину
всеобще-божественной юрисдикции которого подчинено всё и вся.
Многословность разумеется не случайна и она лишь выражение
опыта, который говорит о главной проблеме, неизменно стоящей в рост перед познающим
субъектом: человек не понимает ни других, ни себя самого, но это ещё часть беды.
Другая и много большая часть – и это воистину беда – он не
хочет понимать ни себя, ни других, ибо потрясающе слабоумен и туп в своём
самомнении «венца творения».
Иначе говоря, человек, как правило, настолько ограничен, что его «понимание» чего-либо
– может быть в равной мере названо «непониманием» и отношение между обоими понятиями настолько неопределенно, что даже интеллектуальную ограниченность невозможно
как-то определить в границах определенных
форм-понятий. И если постараться как-то совершенно по-простому выразить суть всей
ситуации, то она видимо, в следующем образе, образе обреченного возгласа врача-психиатра: «Какой к черту диагноз, просто – дурак!».
Вот такая простая непростая ситуация.
Ведь именно указанная простота (непростота) вызывает
непростоту (простоту) в оперировании формами и соответственно их понятийном разумении: «как же я могу
сказать, что понимаю что-либо, если я даже не понимаю, что означает «понимать»?
И в таких случаях, видимо, лишь русское сознание – сознание образное и склонное
чувствовать сердцем истину и справедливость – способно разрубить гордиев узел злокачественного
движения в порочно-формальном кругу, в котором непонимание неотличимо от своей
противоположности.
Но пока что проблема и в том, что на любой вопрос и
любое суждение, подразумевающее внутри себя вопрос: «Вы, – понимаете?», ответом скорее
всего будет эдакий бессмысленный смех, которые можно услышать за кадром ситуационных комедий и в кадре неисчислимых дебильных шоу, превращающих
участников в соучастников повсеместного творимого людьми тотального беззакония,
ибо у человечности в мире, видит Бог, несколько иная функция и предназначение.
Что в таком случае говорить о таких нерейтинговых ныне
понятиях как «Истина», «Всеобщее», «Абсолют», которые в прямом смысле содержат – выражая собой – через себя – в
себе бесконечно глубокое вложение неисчислимого числа взаимодействующих
понятий.
Но человек, если даже и пытается понять
что-либо, но совершенно не понимает того, что если основание не
является всеобщим, то даже попытка
договорится о начале, имеющем смысл некоего «начала», имеющего разумное продолжение, – в смысле тех или иных понятий, которые
используются в качестве аргументов никакого смысла не имеет.
Иногда неглупые люди даже говорит о подобном – о необходимости предварительно договориться, о чём далее будет
говорено, чтобы под одинаковыми вербальными формами одного дискуссанта было скрыто хотя бы примерно то же, что скрыто у другого,
чтобы соблюдались элементарные правила и логика взаимодействия.
Но даже эти неглупые люди всё же, как правило, не понимают, что же они говорят, когда говорят о подобном.
Речь, разумеется, идёт о хорошо известном, о
необходимом едином основании относительно
которого должны быть определены все
используемые понятия.
В этом смысле показательны и хороши математические и
вообще так называемые «научные дискуссии», когда предметная область является
хорошо формализованной, т.е. оформленной стройной системой форм, каждая из которых занимает подобающее ей классическое место потому, что не занимает другого.
Но даже и для такого рода форм поиска истины порой случается не совсем обоснованный выбор основания:
«С именем Даламбера связан один
забавный случай. Рассказывают, что, обучая математике очень тупого и очень
знатного ученика и не добившись понимания доказательства, Даламбер в отчаянии воскликнул: “Ну,
честное слово, сударь, эта теорема
верна!” На что ученик отвечал: “Сударь, почему вы сразу так мне не сказали? Вы
– дворянин, и я – дворянин; Вашего слова для меня вполне достаточно”.
Здесь перед нами представлена в общем виде модель «проблемы понимания», если и не в полный рост, то хотя бы в согбенно-полувертикальном
положении: от человека ныне требуется мыслить и понимать творимое собой и
другими, а не просто соглашаться
или не соглашаться, исходя из каких-то иных и кажущихся обоснованными причин.
Иными словами, в явленных ныне и очевидных для всякого мыслящего человеческого существа Скрижалях Всеобщей Воли Сказано:
«Предрассудочность и тупость более не имеют и не могут иметь никакого
оправдания, пришло время сдавать
экзамен на разумность и право называться
человеком и быть им.
Переэкзаменовок не будет, не сдавшие будут отчислены и исключены навечно
из списков тех, кто имеет право быть, т.е. воплощаться в человеческой форме».
Логика воплощений и перевоплощений в нерушимой
законной связи с тем, что человеком совершается в жизни издревле
известна человечеству, и это обычная трансформальная логика, в которой
противоположности «жизни» и «смерти» в причудливом танце-кружении переходят
друг в друга через самих себя.
Единство же обоих – третье из двух возможных – называется «нирваной».
Это не жизнь, и не смерть и не некое «уничтожение»,
нирвана – то, что выше обоих противоположностей, это диалектическое снятие
жизни – смертью, а смерти – жизнью, раскрывающее перед достигшим совершенно неведомые и непредставимые перспективы.
Возвратимся однако же к философии математики, и дабы не оставить дело так, чтобы имя Вейля
не было упомянуто всуе, продолжим строго о том, что сам Вейль говорил по темопредмету нашего внимания:
«Вряд ли кто-нибудь из нас
сочтет удовлетворительным такой способ передачи математической истины, при
котором она предстает в виде сложной цепочки формальных умозаключений и
вычислений, когда мы вынуждены, так сказать, вслепую, наощупь переходить от
одного звена к другому. Мы хотели бы
заранее видеть конечную цель и ведущий к ней путь, хотели бы понять внутреннее
основание, определяющее ход мыслей, идею доказательства, более глубокие
взаимосвязи. С современным математическим доказательством дело обстоит так же,
как с современной машиной или экспериментальной физической схемой: простые
основные принципы лежат глубоко и едва различимы под оболочкой технических
деталей. Феликс Клейн, рассматривая в своих «Лекциях о развитии математики в
XIX столетии» творчество Римана, говорит: «Неопровержимые доказательства всех
утверждений, несомненно, являются краеугольным камнем любой математической
теории. Разумеется, математика сама судит, в каких случаях стоит поступиться
строгостью доказательств. Извечный секрет необычайной продуктивности гения — в
его умении находить новые постановки задач, интуитивно предугадывать теоремы,
приводящие к новым значительным результатам и к установлению важных
зависимостей. Не будь новых концепций,
новых целей, математика с присущей ей строгостью логических выводов вскоре
исчерпала бы себя и пришла в упадок, ибо весь материал оказался бы
израсходованным. В этом смысле можно сказать, что математику движут вперед в
основном те, кто отмечен даром интуиции, а не строгого доказательства». В
методике самого Клейна главным было именно это интуитивное постижение тех
внутренних взаимосвязей и отношений, основания которых различны, но там, где
требовалось напрячь всю мощь изощрений логики, он в известной мере был вынужден
отступать. В речи, посвященной памяти Лежёна Дирихле, Минковский
противопоставил принципу минимума, который в немецкой литературе принято
связывать с именем Дирихле, но который на самом деле был всесторонне разработан
Уильямом Томсоном, другой, подлинный
принцип Дирихле: одолевать проблему при минимуме слепых вычислений и максимуме
наглядных идей; с этого принципа, говорит Минковский, началось новое время в
истории математики.
Но в чем же секрет такого
понимания математических фактов, в чем он состоит? В философии науки ныне вновь предпринимаются попытки противопоставить
понимание, герменевтику как основу наук
о духе, естественно-научному объяснению, и вокруг слов «интуиция», «понимание» возникает некий мистический ореол
как свидетельство их особенной глубины и непосредственности. В математике
мы предпочитаем несколько более трезво смотреть на вещи. Я не могу пускаться
здесь — да это, мне кажется, было бы очень трудно сделать - в подробный анализ
тех мыслительных актов, о которых пойдет речь. Но одну решающую, хотя саму по себе и не достаточную, характеристику
процесса понимания я хотел бы подчеркнуть: различные стороны предмета
математического исследования мы подвергаем естественному разделению, каждую
сторону в отдельности осваиваем, исходя из особого, сравнительно узкого и легко
обозримого набора предположений и затем возвращаемся к целому, подходящим
образом объединяя частные результаты в сложное единство. Последняя,
синтетическая, часть процедуры носит чисто механический характер. Все
мастерство заключено в первой, аналитической части - разделении и обобщении. На
протяжении последних десятилетий математика прямо-таки упивалась всякого рода
обобщениями и формализациями. Однако считать, будто она стремится к общему ради
общего, значит неверно понимать заключенную здесь здоровую тенденцию. Дело
обстоит иначе: любое естественное обобщение упрощает, сокращая допущения, и тем самым позволяет
понять определенные стороны некоторого необозримого целого. Разумеется, вполне может случиться, что
обобщения в различных направлениях принесут понимание конкретного положения
вещей в различных аспектах. В этом случае разговор об истинной основе, истинном источнике этого положения вещей отягчен
субъективным и догматическим произволом».
Выдающиеся мыслители (в данном случае математик и это
очень ценно) даже заблуждаясь, совершенно точно обозначают критические точки роста дальнейшего
и развития некоторой научной дисциплины:
«…различные стороны предмета математического исследования мы подвергаем
естественному разделению, каждую сторону в отдельности осваиваем, исходя из
особого, сравнительно узкого и легко обозримого набора предположений и затем
возвращаемся к целому, подходящим образом объединяя частные результаты в
сложное единство. Последняя, синтетическая, часть процедуры носит чисто
механический характер. Все мастерство заключено в первой, аналитической части -
разделении и обобщении».
Даже отмечая и учитывая некоторые особенности восприятия
того, что такое «синтез» и «обобщение» (как следует, например, из контекста
продолжения цитаты) можно говорить о том, что понимание довлеющего положения анализа у Вейля как, впрочем, и у
любого иного в определенной мере формально мыслящего исследователя, отражает непонимание понятия общего в
математике. Когда Вейль говорит об «общем», то можно видеть прежде всего его
формализм, абстрактность и оторванность от того, что действительно может быть
общим, а главное – должно им быть как основанием:
«Мы хотели бы
заранее видеть конечную цель и ведущий к ней путь, хотели бы понять внутреннее
основание, определяющее ход мыслей, идею доказательства, более глубокие
взаимосвязи».
Если рискнуть (и суметь!) обозреть сферу
математического знания целиком, то
сразу бросается в глаза, что математика исторически как бы лишена своего
истинного, т.е. выявленного единого основания являя собой
разрастающуюся совокупность разнообразнейших форм, взаимодействующих между
собой. И Вейль, когда он говорит, и как показано далее, говорит с горечью об избранном математиками пути «обобщения», то имеет ввиду ту или
иную комбинацию таких форм, которая
становится «основанием» или, по крайней мере, выдается за него произволом
творца такой формы.
Но самым, пожалуй, поразительным является то, что наиболее выдающиеся математические достижения, становясь
ведущими на многие десятилетия, по сути дела не осознавались именно
как такие, которые выявили
в соответствующей мере свои математические основания.
Речь к слову о тех же упомянутых Вейлем – Ф.Клейне,
Римане, Минковском и их достижениях.
Основание – то единое, неименное, на что опирается и благодаря чему
существует всё иное, все формы, в данном случае математические.
Именно с основанием неразрывно связано любое понимание, ибо понимание есть осмысление основания, т.е. основание (всеобщее), которое стало для
самого себя пространством движения мысли и является истинным пониманием.
«Конструктивный опыт перестает подкреплять принципы аристотелевской логики,
когда эти принципы применяются к экзистенциальным или общим суждениям,
относящимся к бесконечным областям, таким, как последовательность целых чисел или
континуум точек. Если же мы примем во внимание логику бесконечного, то нам вряд
ли удастся адекватно аксиоматизировать даже самые примитивные процессы,
например, переход n1 -> n2, т. е. от целого числа n к следующему числу n'. Как
показал К. Гёдель, всегда найдутся конструктивно очевидные арифметические
суждения, не выводимые из аксиом, как бы вы их ни формулировали, и в то же
время аксиомы, безраздельно правящие всеми тонкостями конструктивной
бесконечности, выходят далеко за пределы того, что может быть подтверждено
опытом. Нас не удивляет, что фрагмент природы, взятый в своем феноменальном
изолированном бытии, бросает вызов нашему анализу с его незавершенностью и
неполнотой.»
Что такое аксиомы по сути своей и своему назначению?
Некоторые базовые основные формы, относительно которых и которыми производится
конструирование и построение иных форм.
Аксиоматика это форма осуществления формального определения, а точнее квазиопределение на фундаменте, так
называемых, неопределимых понятий.
Неопределимое понятие – это наиболее общее, самое общее понятие, на котором
осуществляется и из которого выводятся все иные. Для математики, например, это:
«точка», «прямая», «множество» и т.д:
«… обнаруживаем, что определить все математические понятия невозможно.
Одно определяется через другое, другое через третье и т. д.; где-то мы должны
остановиться. («Портной учился у другого, другой у третьего, да первый-то
портной у кого же учился?» — справедливо замечает г-жа Простакова.)
Рассказывают, что известный одесский математик С. И. Шатуновский, приводя
определение все новых и новых понятий, в ответ на повторные вопросы «А что
такое то-то и то-то» наконец не выдерживал и сам спрашивал: «А что такое «что
такое?»»
Давайте задумаемся об устройстве толкового словаря какого-либо языка —
русского, английского и т. д. В нем одни слова
определяются через другие, другие через третьи и т. п. Но поскольку слов в
языке конечное число, то неизбежно возникает круг (т. е. ситуация, в которой
слово определяется в конечном счете через само себя). Избежать такого круга
можно лишь одним способом: оставить некоторые слова без объяснений. В некоторых
словарях так и делают. Так же, разумеется, обстоит дело и с понятиями
математики. А именно, если только не допускать порочного круга, некоторые понятия
должны остаться без определения. Спрашивается, как же могут быть усвоены эти
понятия. Ответ: из непосредственного наблюдения, из опыта, из интуиции. Нет
нужды напоминать, что формирование общих, абстрактных понятий в мозгу человека
— сложный процесс, принадлежащий более психологии, нежели логике. Эти понятия,
усваиваемые не из словесного определения, а из непосредственного личного опыта,
естественно называть первичными понятиями, или категориями, математики. К числу
таких категорий относятся, например, понятия точки, прямой, множества,
натурального числа и т. д.
При составлении перечня (вряд ли могущего быть вполне отчетливым)
категорий (первичных понятий) математики следует соблюдать известную
осторожность. Иначе число первичных понятий будет неоправданно велико в
нарушение принципа «бритвы Оккама».
Аксиоматика вообще невидимо и незаметно пронизывает
всю практику человеческой активности, с самих её основополагающих
познавательных основ.
Это – (указывается ложка) – «ложка».
Это… (оператор отношения) «ручка».
Это – (оператор) – стул.
Это – «стол»…
Такого рода аксиомы истинны прежде всего потому, что прежде всего практичны.
Базовый познавательный формализм, который находит себя
в завершенной форме в формальной логике: «А это А», то есть «некоторая форма «А»
должна рассматриваться тождественной самой себе» утверждается всей массой
отношений формы «А» со всеми иными формами.
Но это же отношение утверждает и прямо противоположное и важнейшее, и являющееся сущностью познания, без которого самого
познания не было бы: все различные формы в той или иной мере едины, то есть наряду с познавательной аксиомой «А»
есть «А», а вообще говоря именно
благодаря ей, действует и прямо противоположная – ««А» не есть «А»» или ««А»
всегда есть нечто иное, чем оно есть» приходя наконец к пределу в котором – в
границах рассматриваемой меры всеобщности – едино всё: «А есть не-А».
Иными
словами, некоторое А, некоторая форма не
была бы собой, если бы не была в сущности себя всем иным.
Ложка это, несомненно, просто «ложка», но вместе с тем
это и «столовый прибор», и некоторый «культурный артефакт», и «обрабатываемая
станком деталь», и продаваемый (покупаемый) «товар», и «подарок», и «археологическая
находка», и абстрактный «предмет», и прочее
иное неисчислимое, бесконечное число иных форм и отношений, в которые
вступает, и не может не вступить понятие ложка. И именно эти отношения, в
которых качество собственно «ложечности» уже почти утеряно и исчезающее, бесконечно мало всё ещё так же определяет понятие ложка, как и простейший и
понятнейший познавательный оператор, благодаря которому ребенок учится
познавать мир: «это - ложка».
Познание это последовательное раскрытие содержания
формы и обнаружение под формой некоторого понятия всего иного мира отношений и форм,
которые скрыты в глубине формы.
Точка это, как всем известно, … точка.
Но точка это, например,
и «окружность бесконечно малого радиуса», и «область пересечения секущей
плоскости и вершины конуса». И в качестве своей формы-инварианта математическое понятие «точка»
– раскрываясь и определяясь «оператором сечения» становится: параболой, гиперболой, окружностью… Если же сечение
проходит через вершину и параллельно оси конуса точка превращается в угол.
Представление и понятие. Условием
понимания фундаментальной универсальности понятия предела является понимание
сущностного отношение этих противоположных друг другу форм познания.
В этой связи интересен
следующий вопрос: в каком случае, когда перестает действовать формальная логика?
Формальная логика и в
частности закон исключения третьего так
сказать «перестают действовать» и переходят в логику аформальную лишь в том
случае, если существует третье, которое объединяет различающееся
(противоположное) собой, сливая их в
целое.
Очевидно, что логика
появления «третьего», объединяющего как две противоположные формы, и в общем
случае бесконечное число просто
различающихся альтернатив – это логика
бесконечного.
Например,
- «Сапоги», «лапти»,
«мокасины», «кеды», «кроссовки»…., - «обувь»;
- «Красный», «зеленый»,
«фиолетовый», «голубой», …., - «цвет».
- «Автомобиль»,
«газонокосилка», «лифт», «самолет», «пулемет», …., - «машина».
Формула реализации:
«Единичные есть особенное».
Особенное в таком случае является охваченным бесконечным пределом или
замкнутым (предельно нелинейным) пространством бесконечного числа единичностей, которые и образуют данное
пространство и определяют его понятийную (качественную) метрику.
Качество в таком случае выступает как характеристика
пространства, то есть пространственная
метрика или мера формы определенности бесконечной
количественности некоторого рода.
Суть рассматриваемой нами
сейчас проблематики, несмотря на свою простоту и то, что мы уже касались этой
темы, вовсе не тривиальна.
Рассмотрим предмет
определения, как особую форму достигнутого и включенного в ряд, т.е. охваченного
предела подробнее.
Кажущаяся элементарность и
привычность известного ещё из школьной программы базового понятия математического анализа – понятия предела является результатом
рассудочно-формализующего или, иначе говоря, аналитического разумения.
На деле же, «математический
анализ» – оказался очень точным наименование научной
дисциплины, выходящей далеко за пределы математики как таковой, призванной
познавать законы отношений абстрактных математических форм. И такая дисциплина
появилась именно тогда, когда должна была появиться.
«Значение
теории пределов для логики
1. Здесь
перед нами также, по-нашему, огромный дар логике от математического анализа. Мы
покамест оставим в стороне категорию производной в целом, ибо в дальнейшем ей
посвящается у нас отдельный параграф. Но о категории предела, входящей в производную,
необходимо сказать подробнее уже сейчас. Эта категория, как мы видим,
привлечена у нас не больше и не меньше как для изображения логического
отношения между мышлением и чувственностью.
Невозможно
себе и представить все ухищрения ученых в вопросе о взаимоотношении мышления и
чувственного представления. Можно
сказать, вся история философии, особенно Нового времени, есть история разных
теорий о взаимоотношении мышления и представления или, в дальнейшем, мышления и
ощущения. И результат всех этих теорий довольно-таки плачевный. Это — априоризм
и сенсуализм с бесконечными оттенками между ними. И это почти всегда подмена
логической точки зрения разными натуралистическими исканиями, что из чего и как
произошло. Но что бы и как бы из чего ни происходило, логическая значимость
этим не определяется. […] Пусть общее понятие «происходит» из чувственного опыта.
Ну и что же из этого? Прежде всего, такое решение логической проблемы общего
понятия не имеет никакой возможности ответить на критику Канта о том, что
всякое отдельное чувственное восприятие пространственно-временной вещи уже
предполагает априорные формы пространства и времени. А во-вторых, какое же это имеет
отношение к логической природе мышления? А если известная теорема приснилась
мне во сне в готовом виде, значит ли это, что данная теорема неверна?
Вместо всех
этих жалких ignorationes elenchi математический анализ
дает нам точную и сильную, яркую картину именно логического отношения между
понятием и представлением. Спросим себя, какой смысл имеет в науке
чувственное представление? Не само же по себе, в самом деле, оно имеет тут
значение. Ведь наука — это установление законов, нахождение общих соотношений,
т.е. то самое, на что совершенно не способно чувственное представление. Хороша
была бы физика, если бы она не шла дальше тех скоростей, которые можно уловить
глазом! Не только о скорости света мы никогда не узнали бы и не могли бы о ней
учить как о чем-то реальном; но мы вообще о скоростях больших <...> м
[етра] в секунду не могли бы иметь никакого представления или должны были бы отрицать
их реальность. Но если не само по себе имеет значение для логики чувственное
представление, то какое же еще? Уже не такое ли, о котором говорят т.н. эмпирики,
что отдельные чувственные представления сливаются в одно общее представление,
т. е. такое значение, которое сводится к тому, что они бесследно гибнут и
расплываются в мышлении? Однако тут мы, конечно, должны защитить чувственное
представление от такого его оправдания. Чувственное
представление вовсе не гибнет; оно
нужно для науки, оно—орудие науки; без него нет и самой науки. Но в чем же
тогда дело? В чем же тогда значимость, и
именно логическая значимость, представления в сравнении с понятием?
2. Я не знаю более совершенного способа и
сохранить для науки чувственное представление, и в то же время ограничить его в
сравнении с научным понятием (так ограничить, как оно фактически ограничено в
своем научном употреблении), кроме
толкования понятия как предела и представления как переменной величины, стремящейся
к пределу. Что чувственное представление с такой точки зрения является
чем-то ограниченным, это ясно. Но вместо неясного термина «ограниченность» мы
получаем тут яснейшую категорию из теории пределов, именно категорию переменной величины, стремящейся к пределу. Такая
величина всегда приблизительна. Она никогда не
достигает своего предела, но зато и может приближаться к нему с любой точностью. Таким образом, по самой
природе своей она есть нечто становящееся.
Переменная величина имеет предел, говорят математики, если разница между ней и
ее пределом может стать меньше любой заданной величины, т.е. вечно стремится к
нулю. Что этим чувственное представление буквально спасается для науки, это совершенно ясно. Вместо расплывчатого
пятна неизвестно чего, вместо абсолютной текучести дряблого чувственного марева
представление получает определенную
закономерность, оно получает научный смысл, его уже нельзя просто
отбросить, оно — настоящий фундамент науки. Но в то же время все его логическое
значение держится, по нашей теории, только его пределом, т. е. понятием, общим,
которое им управляет, как в математике предел управляет соответствующей ему переменной
величиной. В этом пределе нет ровно ничего таинственного или сверхъестественного.
Это—самая обыкновенная конечная величина. Но он безусловно дает закон для соответствующей переменной величины,
точь-в-точь [как] в реальной и истинной науке: мы имели массу всяких
чувственных представлений, но весь их смысл заключается только в том, чтобы мы
добыли из них закон природы или общества, получили бы то общее, которое их
осмысляет и для которого они являются материальной базой.
3. Имея все это в виду, попробуем дать
более точное логическое раскрытие
понятия предела. Способов такого раскрытия несколько, и тут возможно
употребление самых разнообразных категорий. Предлагаемая нами конструкция
отнюдь не единственная и, вероятно, не наилучшая, так как вопрос этот почти не
обсуждается в логике; и дружная разработка его, конечно, тотчас же обнаружила бы
и другие, более совершенные подходы. Однако за отсутствием исследований этого
вопроса в философии попробуем дать тут некоторое логическое построение с
единственной претензией — только на первое приближение к истине.
Первое, что представляется нам тут
очевидным, это то, что предел вовсе не есть ни
только конечная, ни только бесконечная величина. Хотя всегда было и много
охотников свести предел на конечное число на том основании, что он фактически
может быть конечным числом, это есть, само собой разумеется, просто устранение
самой проблемы. Когда мы имеем то или иное число натурального ряда, мы,
конечно, вовсе не имеем никакого понятия предела и не нуждаемся в нем. Предел
интересен вовсе не своей конечностью. Предел, какой бы величиной сам по себе он
ни был, интересен тем именно, что он есть предел,
граница—для чего? Для некоторого
бесконечного непрерывного процесса. Если нет того, что стремится к пределу,
нет и самого предела. Однако что такое это стремление? Оно не может быть рядом
конечных и взаимно изолированных величин. Это было бы не стремлением, а мертвым
покоем. Следовательно, здесь необходима именно непрерывность. И потому предел есть синтез конечного и бесконечного
в абсолютно неделимом и непрерывном смысле: он есть и нечто устойчивое,
определенное, конечное и в то же время требует некоего процесса, стремления,
протекания, но—так, что в результате он есть некая совершенно неделимая
цельность и единичность, без всяких разрывов и различий».
Фундаментальная математическая аксиоматика
с её непререкаемым требованием непротиворечивости на деле не так уж далеко ушла от обыденности аксиоматики, той обыденности которой
человек воспитывается и в конечном счете образуется дабы гордо носить звание разумного
существа.
Предельный,
то есть бесконечный переход с одновременным охватом бесконечного в качестве
целого, подводит под аксиомы
любого рода, под любую систему аксиом любого формы особый логический фундамент, который собственно и является истинным
смыслом соответствующего понятия, причем само
движение познания понятия, является самодвижением самообоснования понятия,
а познание понятия становится, таким образом, познанием истины.
«1) Диалектика есть сфера чистого
смысла. В этом она отлична как от всякой натуралистической метафизики,
оперирующей гипостазированными абстрактными понятиями, так и от отдельных наук,
основанных на эмпирическом изучении через чувственные восприятия множества
фактов и индуктивном их обобщении. Диалектика не гипостазирует, не овеществляет
абстрактные понятия (ибо в ней и нет ничего, кроме понятий), не изучает
эмпирическое множество текучих фактов (ибо фиксирует их нетекучий смысл) и не
делает никаких индуктивных обобщений (ибо в сфере смысла все одинаково обще).
2) Диалектика есть
осмысленно-объяснительное конструирование смыслового взаимопорождения отдельных
моментов цельной сферы разума, так что оказывается понятным, каково
логическое происхождение и отдельных моментов смысла, и всей сферы смысла
вообще. Этим диалектика отличается от феноменологии, основанной на описании
изолированных форм смысла, связь и взаимопорождение которых мыслится тут только
натуралистически и отводится в сферу т. н. мира естественной установки.
Диалектика не описывает, но объясняет и выводит не только логическое, но и
алогическое – из цельного единства смысла вообще.
3) Диалектика есть фиксирование в
самопорождающейся стихии смысла завершенных и умно-оптических,
визуально-смысловых оформлений, нерушимо пребывающих в непрерывно подвижной
стихии смысла. Этим диалектика отличается от трансцендентализма типа Когена, основанного на интерпретации
смысла как «чистой возможности», «закона», «принципа», «метода», «постановки
проблемы», «гипотезиса». Диалектика не ограничивается только стихией
становящегося (хотя бы и чисто смыслового) смысла, но признает последнее только
в связи с порождением отсюда закругленных и визуально-данных уму оформлений.
4) Диалектика есть
антиномико-синтетическое конструирование сферы смысла как самопорождающегося и
самопреодолевающегося противоречия. Этим она отличается от т.н. формальной
логики, основанной на законах тождества, противоречия и исключенного третьего.
Диалектика есть конструирование смысла, который сам себя порождает, т. е. смысл
этот есть и порождающее, и порождаемое, т. е. он и тождествен с собою, и отличен
от себя, т. е. закон тождества дополняется тут законом различия в тождестве. И
вообще, никакое определение невозможно без ограничения; ограничение же есть
некоторое отрицание; отрицание же в сфере смысла есть отрицание осмысленного
утверждения. Итак, отрицание и утверждение в сфере смысла как отличаются между
собою, так и отождествляются. След., закон исключенного третьего дополняется
законом неисключенного третьего. И т.д. Отдавши себе отчет в существе и задачах
диалектики, попробуем теперь произвести первоначальные и необходимейшие
диалектические построения, с тем чтобы показать, что учение о множествах есть
не что иное, как именно эти первоначальные и необходимейшие построения в сфере
чистого смысла».
Здесь следует ещё
раз обратить внимание на просто великолепное и по форме и по содержанию и
по их мере гармоничности (простоте) определение диалектики данное А.Ф.Лосевым:
«Диалектика есть
антиномико-синтетическое конструирование сферы смысла как самопорождающегося и
самопреодолевающегося противоречия. Этим она отличается от т.н. формальной
логики, основанной на законах тождества, противоречия и исключенного третьего.
Диалектика есть конструирование смысла, который сам себя порождает…»
И по сути дела простое понимание сущности всеобщего становления именно как движения способно
навести порядок в формальных умах, но уявление сущностной противоречивости мира никак не дается этим умам, которые боятся противоречивости, ибо полагают, что единственной логикой может быть исключительно
формальная логика, как логика не-противоречия:.
«…диалектика есть противоположность формальной логике. Опять-таки, и то
и другое относится и к чистой сфере смысла, и оперирует с чистыми понятиями, а
не с вещами, и дает конструкции тех или других форм мысли и смысла. Но мы жестоко
ошибемся, отождествивши эти два метода. Под формальной логикой мы понимаем
учение о смысле, возникающее на почве т. н. законов мышления, т. е. закона
тождества, противоречия и исключенного третьего. Закон тождества, гласящий, что
А = А или, точнее, что А в одно и то же время и в одном и том же отношении
тождественно А, т. е. самому себе, этот закон, оставаясь в диалектике в полной
силе, добавляется, однако, законом, ему совершенно противоположным, а именно
тем, что одно и то же А в одно и то же время и в одном и том же отношении
различно с собою, нетождественно себе. А и есть А, и не есть А. Соответствующим
образом модифицируются в диалектике и оба другие закона «формальной логики».
Оказывается, сама же мысль, сам разум требует противоречия себе, самопротиворечия,
и сама же мысль, сам разум требует преодоления этого противоречия в еще новом
утверждении. Диалектика, которая не есть логика противоречия,— не есть
диалектика, но — только формальная логика. И [есть] очень много авторов, именующих себя диалектиками и в то же время
совершенно не владеющих этим методом, растворяя необходимую тут антиномику в
систему непротиворечивых, упорно не-тождественных между собою полаганий смысла.
Противоречие, его преодоление и утверждение нового противоречия есть душа и
жизнь диалектики. Поэтому от замороженных и оцепенелых конструкций формальной
логики диалектика отличается именно антиномико-синтетической структурой смысла».
Противоречивости именно как формальной противоречивости действительно следует опасаться и следует
избегать её, так как именно «непротиворечивость» есть базовое правило любой
познавательной игры, но просто следует понимать наличие неформального и
аформального смысла, который в самом себе несёт в качестве своего истинного
содержания понятие «непротиворечивости», которое, очевидно, может быть
собой, т.е. «лишенным противоречия» лишь
тогда, когда
это противоречие находится в основе, существует в качестве достаточного
(необходимого) основания.
Казалось бы речь идёт о совершенно простом и
очевидном, но насколько тяжело и неадекватно видится формальным умам такая очевидность (Вейль):
«Ее интересует не истинность аксиом, а лишь их непротиворечивость; в самом деле, противоречивость apriori лишала бы нас надежды когда-нибудь найти
подходящую интерпретацию», утверждает даже человек, и не просто человек, а выдающийся
математик, который декларирует и обнародует основу основ логики математики
как науки: «Математика — это
наука о бесконечном».
Но именно противоречие, противоречие,
рождаемое бесконечностью любого рода,
уходящей в неясные внутренние континуальные глубины, или вырываясь во внешнюю
бездну бесконечного, даёт истинную фундаментальную
интерпретацию всего математического движения как целого: движение
самопорождение бесконечного – конечным, а конечного – бесконечным, или в
гегелевских терминах: «переход через
самого себя в своё иное (противоположное)».
Это и есть единственная
абсолютная аксиома, аксиома необходимого основания, снимающая саму себя как аксиому, ибо сама себя обосновывает и выводится из
самой себя, находится в фундаменте математики и всего математического знания, впрочем,
как и любого иного знания вообще.
Оператор преобразования – оператор перехода, являющийся самим движением перехода, совпадающим с ним и являющийся ничем иным
как движением познания, движением познающего субъекта, самим субъектом.
Бесконечное становление бесконечности движения во
времени…. Более ничего и никого нет.
Итак, в математике первой и по всей
видимости важнейшей формой отражающей живую диалектику человеческого познания явилось понятие предела.
Именно это понятие стало той
общепринятой, но практически полностью формализованной формой, в котором
наконец в головах ученых обосновывалось и в известном смысле завершилась весьма непростая и драматическая история осмысления
понятия «бесконечного» преимущественно именно как бесконечно уменьшающейся величины, т.е. понятия «бесконечно малой
величины».
«Насущная
необходимость надлежащего обоснования математического анализа остро ощущалась в
конце XVIII в. всем математическим миром, и по предложению Лагранжа отделение
математики Берлинской академии наук, директором которой он состоял в 1766—1878
гг., назначила в 1784 г. приз (который должен был быть вручен в 1786 г.) за
лучшее решение проблемы бесконечности в математике. Объявление об условиях
конкурса гласило:
Своими предложениями, всеобщим уважением и почетным титулом образцовой
«точной науки» математика обязана ясности своих принципов, строгости своих
доказательств и точности своих теорем.
Для обеспечення непрестанного обновления столь ценных преимуществ этой
изящной области знания необходима ясная и точная теория того, что называется в
математике бесконечностью.
Хорошо известно, что современная геометрия [математика] систематически
использует бесконечно большие и бесконечно малые величины. Однако геометры
античности и длже древние аналитики всячески стремились избегать всего, что
приближается к бесконечности, а некоторые знаменитые аналитики современности
усматривают противоречивость в самом термине бесконечная величина.
Учитывая сказанное, Академия желает получить объяснение, каким образом
столь многие правильные теоремы были выведены из противоречивого предположения,
вместе с формулировкой точного, ясного, короче говоря, истинно математического
принципа, который был бы пригоден для замены принципа бесконечного и в то же
время не делал бы проводимые на его основе исследования чрезмерно сложными или
длинными. Предмет должен быть рассмотрен во всей возможной общности и со всей
возможной строгостью, ясностью и простотой.
К участию в
конкурсе допускались все желающие, за исключением членов Академии, Всего на
рассмотрение жюри поступило двадцать три работы. Официальное решение,
опубликованное после окончания работы жюри, гласило:
Академия получила много работ на объявленную тему. Авторы всех работ не
смогли объяснить, каким, образом из противоречивого предположения — о
существовании бесконечно большой величины — удалось вывести так много
правильных теорем. Все авторы в большей или в меньшей степени пренебрегли
требованиями ясности, простоты, а главное — строгости. Большинство из авторов
даже не осознали, что принцип, который им надлежало найти, должен был не
ограничиваться дифференциальным исчислением, а распространяться также на
алгебру и геометрию, рассматриваемые в духе древних.
Учитывая изложенное, Академия считает, что ее требования удовлетворены
не полностью.
Тем не менее жюри нашло, что в наибольшей мере удовлетворил требованиям
участник конкурса, представивший работу на французском языке под девизом
«Бесконечность — пучина, в которой тонут наши мысли». Ему и присужден приз.
Победителем оказался швейцарский математик Симон Люилье. В том же 1876
г. Берлинская академия опубликовала его «Элементарное изложение высшего
анализа». Несомненно, решение, принятое математическим отделением Академии, по
существу было правильным. Ни в одной из других работ (за исключением работы,
представленной Карно; см. гл. VII) даже не делалось попытки объяснить, каким
образом в математическом анализе исходя из ложных посылок удается вывести так
много правильных теорем. Люилье, несомненно, заслуживал награды, хотя основная
идея его работы была далеко не оригинальна. По словам самого Люилье, его работа
представляла «развитие идей... бегло намеченных Д'Аламбером и как бы изложенных
в его статье «Дифференциал», опубликованной в «Энциклопедии», и в его сочинении
«Разное». Во вводной главе своего сочинения Люилье излагает слегка
усовершенствованный вариант теории пределов. Впервые в печатном тексте он ввел
для обозначения предела символ lim. Производную dP/dx (ранее встречавшуюся как
отношение k/h) Люилье обозначал lim ΔΡ/Δx, но вклад самого Люилье в теорию
пределов был крайне незначительным.
Хотя почти каждый математик XVIII в. предпринимал попытку обосновать
математический анализ или по крайней мере высказывал свое мнение по поводу
столь важной проблемы, а два-три математика были на верном пути, все усилия
оказались тщетными. Математики XVIII в. либо умышленно обходили все
сколько-нибудь важные и тонкие проблемы, либо просто не замечали их. Различие
между очень большим числом и бесконечно большой величиной они ощущали с трудом.
Математикам XVIII в. казалось очевидным, что теорема, которая выполняется при
любом конечном п, должна выполняться и при бесконечном п. Разностное отношение
k/h [см. выражение (3)] они охотно заменяли производной, а сумму членов вида
(7) с трудом отличали от интеграла. Переход от конечного к бесконечному как в
одну, так и в другую сторону совершался ими необыкновенно легко и просто. Суть
математики XVIII в., пожалуй, наиболее точно выразил Вольтер,
охарактеризовавший [математический] анализ как «искусство считать и точно
измерять то, существование чего непостижимо для разума». Предпринимавшиеся на
протяжении века попытки строгого обоснования анализа, в особенности попытки,
предпринятые такими гигантами науки, как Эйлер и Лагранж, лишь окончательно
запутали и завели в тупик как их современников, так и математиков последующих
поколений. В целом подобные попытки оказались безнадежно ошибочными — от них
можно было бы прийти в отчаяние и усомниться в том, что математикам вообще
когда-нибудь удастся разрешить проблему обоснования анализа».
Мы – конечно же, зная то, что мы уже знаем, можем утверждать, что т.н. «проблема обоснования анализа» это простое выявление в
анализе – синтеза как его необходимого
и достаточного основания. Так же нам уже известно, что аналитическое
действие, подчеркнём, – любое аналитическое действие – как
действие различающее и расчленяющее, как действие формального дробления-обособления
объекта внимания может перейти в своё противоположное единственным способом.
Этот способ – переход через пропасть, через бесконечное,
через бездну бесконечности.
Соотношение аналитичности,
рефлексия аналитичности как некоторого качества с самим собой взятое как
целое и всеобщее, рождает иное и противоположное качество – качество синтетичности действия.
В основе обоснования
математического анализа в форме «предела» находится совершенно особое аналитическое
действие.
Его особость именно в том,
что это действие движения мысли, которая одновременно выявляя бездну бесконечного в том, что формальному уму
кажется «непоправимо конечным», этим же выявлением – отрицает-преодолевает её, достигает и охватывает бесконечность именно как
предел беспредельного, являющийся необходимым диалектическим основанием любой конечной
математической формы.
Уже сама простая линейная натуральная
числовая последовательность – если видеть её не только лишь как застывшую форму
– но как движение изменения, самодвижение, импульс одновременности утверждения-отрицания
некоторым числом любого иного натурального числа….
Возьмём «5»…
«Число
«пять» может быть и конечным числом натурального ряда, и дифференциалом, и
интегралом, и производной в зависимости от практики мышления. Само по себе «пять» ровно ничего не
значит, или, если выражаться точно, оно ровно ничего не значит познавательно для числа. Всякий смысл
есть всегда смысл чего-нибудь, что
уже не есть просто самый смысл, но дается самостоятельно, практически».
Мы понимаем, что берём числа (в данном конкретном случае
натуральные) не формально-арифметически и даже не аформально, а трансформально.
Но осуществляя осознанный переход от формального и аформального к
трансформальному, мы тем самым выходим в
особое пространство мысли, в нашем случае математическое пространство, в котором
и обнаруживаем весь комплекс категорий охватываемый математическим
трансформальным:
«Теперь мы отбрасываем в сторону
как арифметическое, так и трансфинитное
построение числа и сосредоточиваемся исключительно на инфинитезимальном. Что мы тут должны предпринять, чтобы получить конкретные результаты?
Конкретность требует ясных разграничений
и четких переходов между разграниченными элементами. Число, как первейшее
такое разграничение, является, согласно
предыдущему, как раз таким переходом от одного к другому. Ясно, что и в инфинитезимальной области первичное различение должно быть именно таково: одно
(бытие, «нечто», «это», акт полагания,
изолированное и простое утверждение), становление (переход) и ставшее (исчерпавшее себя и
первичное одно и потому остановившееся,
завершившееся одно). Здесь также только практика может решить, когда и где применить ту или другую
категорию и каково различие возникающих
здесь инфинитезимальных чисел.
Именно соответственно этим трем
категориям мы получаем здесь три
основных инфинитезимальных понятия: бесконечно-малое, непрерывность и предел. Тут, разумеется, может идти
долгий спор по части терминологии.
Однако, по-видимому, не должно вызывать сомнения, что если мы берем становление с точки зрения «бытия», т. е. с точки зрения «нечто», «этого», то тут
мы должны получить «становящееся нечто»,
«становящееся это», некое бытие или что бы то ни было именно в процессе непрерывного становления. Но что же это тогда такое, если не бесконечно-малое, которое как раз и определяется как то, что «может стать»
меньше любой заданной величины? Нам
кажется, что также ясна и непрерывность,
которая есть становление как именно
становление, т. е. положенное, утвержденное становление, и предел, который определяется именно как то, к чему вечно стремится переменная
величина, и в котором стремление,
следовательно, взято именно с точки зрения ставшего.
Мы опять-таки настаиваем на том,
что теоретически совершенно не
существует никакой разницы между бесконечно-малым, непрерывностью и пределом,
ибо теоретический и смысловой состав этих категорий совершенно один и тот же. И только практика может решить вопрос, на что тут можно и нужно обратить внимание, какую категорию акцентировать,
подчеркивать, класть в основу и какую
отодвигать, брать только в виде фона, допускать только как материал для осмысления другими категориями. Словом, эти категории тоже изомерны.
Говорится: бесконечно-малое есть
то, что может стать меньше любой
заданной величины, или что имеет своим пределом нуль. А что такое предел? Предел для переменной
величины есть то, разница между чем и
переменной величиной может стать меньше любой величины, или, что то же, стремится к нулю. А что такое непрерывность, напр. непрерывная функция?
Функция непрерывна в данной точке тогда,
когда бесконечно мало ее приращение в случае бесконечной малости приращения ее аргумента. Вот три определения. По своему категориальному составу это совершенно одно и то же определение: везде тут 1) то, что стремится к пределу,
2) предел, к которому происходит стремление, и 3) самое стремление. В первой
категории на первом плане то, что стремится, но тут же указано и на самое
стремление, и на предел этого стремления. Во второй категории подчеркнуто то,
куда стремление, но тут же сказано и
о том, что именно стремится, и о самом стремлении. И наконец, в третьей категории подчеркнуто самое стремление (или, точнее,
соотношение двух стремлений, поскольку определялась непрерывная функция), но тут же сказано и о
бесконечно-малом, т. е. о нулевом пределе, не говоря уже о том, что
стремится тут именно аргумент и функция,
т. е. нечто. Следовательно, основное и
существенное содержание понятий бесконечно-малого, непрерывности и предела—одно
и то же. Не то, что эти понятия только предполагают одно другое, но
они просто тождественны по содержанию,
и разница тут только в порядке и форме комбинации одних и тех же категорий, т.
е. разница тут только, следовательно, структурная. Только практика может решить, где тут бесконечно-малое, где
предел и где чистая непрерывность.
10. Только после всех этих разграничений и различений мы можем судить о
месте дифференциала, производной и интеграла на фоне общелогической теории
числа.
Разумеется, поскольку мы вовсе не задаемся тут целью дать логику математического
анализа как системы, а интересуемся только некоторыми его категориями в
применении к логике, мы не будем подробно анализировать все эти три, только что
полученные нами категории — бесконечно-малого, непрерывности и предела, а
сосредоточимся только на последней.
Мы берем инфинитезимальную
категорию предела и смотрим на нее теми же самыми расчленяющими глазами, какими
смотрели и на число вообще, и на его инфинитезимальный тип. Тут мы тоже
расчленим 1) «то, что», 2) «то, как» и 3) «то, куда», т.е. «нечто» (бытие),
становление и ставшее.
Будем говорить о пределе (а
всякий предел уже есть соединение того, что стремится к пределу, с самим этим
стремлением, т. е. синтез конечного и бесконечного) и будем его рассматривать,
считать как «то, что стремится к пределу». Как предел, это есть нечто
устойчивое и, в частности, конечное. Однако в то же время это не есть конечное
в абсолютном смысле, но то, что само вовлечено в стихию непрерывного и
бесконечного становления. Это дифференциал,
который как таковой есть переменная величина, но который в основе все же есть
синтез конечного и бесконечного, и синтез — типа предела, поскольку в его
основе лежит производная (а она всегда есть предел).
Далее, продолжаем говорить о пределе. Но на этот раз пусть наш предел
будет не тем, что еще только стремится к своему пределу, но самим этим стремлением, или
становлением. Это есть производная, которая есть прежде всего предел; но это не
просто предел, предполагающий соответствующее становление, а предел отношения двух становлений, т. е. такой
предел, который предполагает рассмотрение одного становления с точки зрения
другого становления, т. е. основан на становлении становления, т. е.
рассматривает становление именно как становление. Совершенно ясно, что в ряду инфинитезимальных категорий предельность
тут дана с сугубым выдвиганием на первый план именно становления. Производная в логическом смысле есть именно метод становления дифференциала
некоторым новым пределом, который и есть интеграл. Интеграл тоже есть прежде всего предел, как и дифференциал и
производная, т. е. одинаково с ними синтез конечного и бесконечного. Однако из
трех основных категорий в нем подчеркнуто не то, что становится, и не самое
становление, но ставшее, то, чем
стало становящееся, исчерпавши всю свою бесконечность и тем дойдя до своего
предела.
Мы и тут настаиваем на полном
существенном тождестве дифференциала, производной и интеграла. И только
практика решает, что тут надо выдвинуть из трех моментов, одинаково данных во
А. Ф. всех трех случаях, то ли, что стремится к пределу, самое ли стремление
или то, куда идет это стремление, или его предел. Все дело, следовательно, в
структуре этих понятий или, точнее, в разных структурах одного и того же
понятия.
Можно сказать еще и так, как мы сказали, выставивши метрическую точку
зрения на инфинитезимальное число. Можно сказать, что различие дифференциала,
производной и интеграла зависит от того, чем
мы будем их измерять, от единицы измерения. Это есть только другой способ
для выражения принципа практики. Мы можем измерять общее инфинитезимальное
число, взятое как предел, при помощи отдельных «единиц». Мы можем взять самую
эту операцию «счета». И мы можем взять результат, то, что получается после
такого инфинитезимального счета наших инфинитезимальных единиц. Из общего
инфинитезимального числа, взятого по типу предела, получаются три указанные
выше категории—дифференциала, производной и интеграла».
Итак, число «5». В
соответствии с тем, что «…основное
и существенное содержание понятий бесконечно-малого, непрерывности и
предела—одно и то же»,
попробуем увидеть его и как нечто единое, объединяющее указанные понятия.
«5» – финал развертывания бесконечности процесса приближения, перехода от числа «4» - (4,0000000000000…
―> 4,9999999999999…)
Этот процесс незавершаем, по причине своей
бесконечности и тем самым отсутствия границы,
но, тем не менее, самой логикой такого отсутствия и ей
как необходимым основанием – завершен.
Необходимо лишь видеть рассматриваемую бесконечность как целое, и тогда эта целостность, как граница бесконечности диапазона (4,0000000000000… ―> 4,9999999999999…),
– становится «пятью»…
Цифра «5», целое число «5»,
константа «5» - это предел становления перехода от целого положительного числа «4» к целому положительному числу «5»,
продолжающий оставаться становлением, то есть движением перехода.
Таким образом, тайна
трансформальной логики, если конечно есть необходимость говорить о тайне,
проста и в буквальном смысле предельно-открыта,
и она в уже знакомом нам, в том, что всё
есть становление и что открытость эта – предельна.
Как это понимать?
Например так, как понимаются
так называемые «предельные точки»:
«Предельная точка множества А, такая точка x пространства, сколь угодно
близко от которой имеются отличные от x точки множества А, т. е. в любой
окрестности которой содержится бесконечное множество точек из А.
Характеристическим свойством П. т. множества A является существование по
крайней мере одной сходящейся к ней последовательности различных точек
множества А. П. т. множества А не обязана ему принадлежать. Так, например,
всякая точка числовой прямой является П. т. для множества А рациональных её
точек:
ко всякому как рациональному, так и иррациональному числу можно подобрать
сходящуюся к нему последовательность различных рациональных чисел».
«Пять» - это исчезающая, буквально
растворяющаяся в бесконечности граница между: 4,9999999999999…
и 5,0000000000000…
«Почему граница есть синтез
идеи и ее инобытия, или идеи и факта,
или, выражаясь в самой общей форме, бытия и небытия. Бытие, осуществляясь,
отличается, отталкивается от небытия; и как только это отличение
заканчивается, бытие получает определенность, т.е. сформулированность,
при помощи предела, границы. Определить для диалектики всегда значит ограничить,
ибо без точного проведения границы со всем бытием, не относящимся к
определяемому бытию, т. е. с инобытием, с небытием, не может состояться и фиксация того, что входит в
определяемое бытие, т. е. не может состояться
само определение. Итак, граница, определенность есть первый и ближайший
законченный результат синтезирования бытия и небытия. Но если это так, то совершенно бесполезно
ставить вопрос о том, к чему относится граница—к бытию или к небытию. Часто
затрудняются вопросом о том, к чему относится граница, т. е. окружность круга,—
к самому ли кругу или к окружающему его
фону. Тут может быть только
диалектическое решение вопроса. 1) Граница бытия есть только потому граница бытия, что она
есть момент самого бытия. Иначе бытие
окажется лишенным границы и, следовательно, потеряет определенность. 2) Граница
бытия относится к небытию, потому что создающее эту границу есть именно небытие, и без наличия
небытия не было бы ничего, от чего бытие
отличалось бы, т. е. не было бы самой
границы. 3) Граница бытия не относится к
бытию, потому что бытие есть само еще только то, что нуждается в определении и ограничении, и
внесение границы бытия в состав самого бытия потребовало бы наличия еще новой
границы для определения бытия, которая уже не входила бы в состав самого бытия. 4) Граница бытия не относится к
инобытию, или небытию, и не составляет
его части, потому что, составляя часть инобытия, она и оставалась бы в недрах
инобытия, и не выходила бы для встречи с бытием и для его ограничения. Следовательно, граница бытия есть и бытие, и небытие и не есть ни бытие, ни небытие, и все это
— при совершенно однозначном употреблении всех этих терминов. Граница потому и
есть синтез бытия и небытия, что она одновременно есть и то, и это и ни то, ни
это. Такова природа и всякого
диалектического синтеза — в отношении соответствующих тезиса и антитезиса».
Формальное и трансформальное
различие понимание цифры «5» как целого числа лишь в том, что «5», будучи непрерывностью-стремлением-пределом, является всем указанным, прежде всего,
является пределом; но аформальный
смысл понятия «предел» в его отношении с собой, т.е. со своим необходимым
основанием ведёт к тому, что предел («5») одновременно принадлежит-и-не-принадлежит охваченной и этим завершающейся-и-завершенной
бесконечности; предел завершает
(становление) бесконечность –
4,99999999999…, но и начинает (становящееся-ставшее)
следующую бесконечность – 5,00000000000…
Таким образом, число «5»
являет собой некоторое «точечное пространство» одновременно принадлежащее и не
принадлежащее обоим интервалам.
Кратко говоря и формульно выражаясь,
числовая форма «5» есть не только «5», но нечто иное формально неотличимое от
«5», а если выразиться точно,т.е.математически: «5» + нечто.
Что же это «нечто» собой
представляет?
Очевидно, что в числовом
смысле это может быть лишь числовой разностью:
«5–5=0»…
Но «0» в выражении количественного
отношения двух величин также есть лишь формальная фиксация формального результата предельного перехода некоторого значения,
предел которого и равен «0».
Предел чего равен «0»?
А) Предел бесконечно малой (т.е. стремящегося к нулю действительного числа);
Б) Предел комплексного числа, мнимая компонента которого стремится к
нулю.
В) Предел комплексного числа, действительная и мнимая компоненты которого
стремится к нулю.
Так, по крайней мере,
проявляет себя логика предела как весьма
необычного, обращаем внимание, движения стремления к некоторой величине,
которое оказывается в результате… данной величиной. Движение, становящееся – обращаем внимание неподвижностью
количественной формы, и разве ни странно, что становящееся именно с точки зрения формальной логики?
Разумеется, странно. Но
формальные математические умы, увы, удовлетворяются простым игнорированием
такой странности и отрицая само движение просто
берут результат движения к пределу, который оказывается неподвижностью его формального значения.
Обратим ещё раз внимание и
на то, что формальная логика становится аформальной и трансформальной тогда,
когда появляется бесконечность любого рода, будь то бесконечно малое или бесконечно
большое. Интересно, что даже терминологически понятие «бесконечно малая»
(«бесконечно большая») противоречиво,
ибо содержит в себе и выражает собой количественное отношение качества «больше» («меньше»), имеющего смысл лишь для конечных и неподвижных
числовых величин.
Итак, «5» – это предел, что означает исчезающая, подвижная, колеблющаяся,
вибрирующая как бы с «бесконечной
частотой» и «бесконечно малой» амплитудой «точечное» пространство, которое отделяет, но одновременно соединяет два целостных и равных друг
другу интервала, граница двух бесконечных интервалов, которая одновременно
принадлежит и не принадлежит обоим интервалам.
Обобщаем сказанное на любое
целочисленное значение, ибо нет ни малейших логических причин не делать этого.
Любое положительное целое
число как математическая форма, которой приписывается рассудком неподвижность и неизменность, то есть все целые числа являют собой т.н. «константы»,
но в действительности константа является некоторым пределом или границей которая обладает особым количественным качеством отличным
от качеств чисел, которые включены во внутренние
пределы данного целого положительного числа, являющегося его границей.
Стоит при этом напомнить, дабы дать известную возможность
избавиться от всепоглощающего и довлеющего формализма рассудочности, что
некоторое целое число – это не просто «исчезающая в бесконечной пучине»
подобных себе всех иных точек на числовой прямой, как это видится формально, но
содержательно есть «определенное количество». Это означает, что число «5» в
себе как форме содержит бесконечное
число иных чисел диапазона (0,5) и является ничем иным как формой-содержания, и именно формой движения содержания.
Таким образом предел есть прежде всего предельная
форма, как форма принимающая на себя и в себя понятие предела есть форма становления содержания. Иначе говоря, бесконечное, но имеющее предел движение
содержания, которое суть количественная мера интервала (0, 5) оформляет себя формой, которая становится пятью («5»). Но качество становления как движения выявляет то, что
данная числовая форма, будучи антиномией «предела беспредельного» (как бы) свертывает
пространство своего содержания, показывая этим, что такое «форма» вообще.
Итак, «предел» некоторого целого положительного числа является границей
формы числового (количественного) коллапса линейного пространства; именно делает возможным завершение незавершаемого и ограничивает
(охватывает) то, что не имеет границы и формально не может быть охваченным.
Ситуация антиномии, которая постоянно используются в качестве особого противоречивого или аформального
(трансформального) определения (предел – беспредельного, охват – неохватного) действительно возникает и является
результатом (рефлексивно-порождающей или самопорождающей себя как результат)
причины - одновременности существования предела как – вдумываемся! – предельно-о-пределённой-границы в
двух различных числовых пространствах. Не что-то или кто-то извне
«делает так», что числовое пространство становится замкнутым, логика наполнения, как логика движения раскрытия содержания этого
пространства искривляет его, то есть само
пространство изменяет свою кривизну наполняясь – определяясь развертывающимися
бесконечностями числовых форм, взаимодействующих друг с другом и, наконец, как
бы под «тяжестью» бесконечной плотности своего содержания свертывается в некоторую целостность. Эта целостность непременно имеет обособляющую границу т.н. «предела» и – очень
важно – отрывается от пространства
числовой прямой, но отрываясь от него, одновременно – остается в нём, ибо в свою очередь становится содержанием
пространства большего количественного ранга.
Здесь уже можно видеть принципиальное отличие
формального понимания «предела», который
так и не выходит из пределов созерцающего вещно-в-себе-пребывающего кантовского представления и являет
собой банальность монументальной неподвижности т.н. «математического мышления» и трансформального,
то есть гегелевского, спекулятивного понимания.
Кроме этого, понимая,
что любое определение есть отрицание,
и любая, рассматриваемая нами числовая форма, допустим, всё то же число пять («5»), определяясь как форма – движением
самоопределения – отрицает все иные целочисленные положительные формы от (1, …, 4) до (6, …, ∞) и, будучи однонаправленной и определенной, вынуждена преодолеть свою собственную определенность и выходить, двигаться, порождать пространство следующего интервала.
Линейное числовое пространство целых положительных
чисел есть пространство иерархий числовых пространств одной из форм числового
коллапса – целочисленного, вложенных друг в друга не-целочисленных
числовых форм, которые являются содержанием и основанием любой целочисленной формы.
То или иное целое положительное число является границей математической числовой формы, во внутреннем пространстве которой свернута и существует как целое та или иная числовая бесконечность,
соответствующая значению достигнутой ей количественной величины, которая
выражается этим числом как своей формой.
Обратим особое внимание и на
то, что данные выше трансформальные определения полностью совпадают с
определениями в предыдущих Главах семантического
коллапса.
Некоторое понятие, являясь формой содержит в себе бесконечное число
своих форм-содержаний, которые искривляют и замыкают пространство понятия,
причём форма, являясь пределом-границей так же принадлежит и не принадлежит своему внутреннему пространству.
Вспомним уже ранее
приведенное (Вейль):
1.
«Пространство бесконечно не только в том смысле, что в
нем не имеется конца; оно кроме того в
любом своем месте бесконечно, так сказать, во-внутрь, и точка в нем может быть
определена лишь путем бесконечного и от раза к разу все точнее и точнее
фиксирующего ее процесса деления.
2.
«Для
заполняющего его многообразия качеств пространство служит принципом их
разграничения, впервые вообще создающим возможность существования различия в
сфере качественного; однако пространство является не только принципом
разграничения, но вместе с тем и принципом соприкосновения, непрерывной связи…»
К п.1: Понятие,
любое понятие – бесконечно, так
как содержательно являет собой бесконечный мир, бесконечно развертывающееся внутренне пространство форм-содержаний,
отношения и движение отношений которых и порождает качество пространственности как общую форму таких
отношений, то всеобщее, что
объединяет собой все формы и все отношения.
К. п.2: Потому не пространство является неким
«принципом разграничения», который одновременно является «принципом непрерывной
связи» – это как раз типично формалистское видение, разрывающее
причинно-следственную связь отношений форм и отрывающее саму форму понятия от
его содержания. Форма – содержательна, «явление есть не просто нечто лишенное
сущности (Wesenloses), а проявление (Manifestation) сущности». Формализм
пытается даже неосознанно вытолкнуть противоречие становления, противоречивость
самого понятия куда-то вовне, хотя бы в пустое инертное пространство, наделив эту внешнюю инертность абстрактно-противоречивой действенностью, которая каким-то неясным образом контролирует
и координирует правила игры форм и их отношени.
Так, именно бесконечность внутреннего пространства того или иного понятия, в том числе и числового,
диктует логику того, что хотя впереди и
бездна бесконечного, требующая бесконечного
времени и усилий для того, чтобы стать преодолимой, но мысль – понятием форм содержаний и их движением охвата
(свертывания, исчерпания и замыкания) данного
понятийного пространственного континуума легко перешагивает и преодолевает границу подобно Ахиллесу в апории
Зенона.
Почему?
А потому, что движение мысли осуществляется одновременно в обоих пространствах –
внутреннем и внешнем.
Почему?
Потому что мысль – это самодвижение волны
(или движение фокус-формы) Всеобщего Пространства в
Самом Себе, то есть в пространстве, ранг
размерности которого сущностно существенно
выше ранга пространств в
которых мысль как мыслеформа мышления
мыслящего воплощается – т.е. проникает
в глубины измерений иерархий миров являющихся формами-проекциями Всеобщего
Пространства Мысли.
Мы рассмотрели ряд важных
аспектов основы математического анализа – понятия математического предела, обнаружив
при этом, что в основе самого понятия предела находится не осознаваемая и
недопонятая логика известная на тот исторический момент как логика гегелевского
спекулятивного мышления.
Таким образом, осуществленное
выдающимися математиками, широко известное и общепринятое на данный момент обоснование анализа стало на деле и первым элементом уже не аналитической, а синтетической математики. В сфере, в которой были
продемонстрированы выдающиеся достижения в виде дифференциального и интегрального
исчислений Всеобщая математическая мысль прикоснулась и даже в известном смысле оперлась на самое прочное основание –
основание Математического Абсолютного, хотя сама этого так и не поняла, а если
и поняла, то сугубо формально.
Можно и нужно при этом обратить внимание на то, когда именно происходило описываемое,
какой период охватывало, и ещё в большей мере обратить внимание на глубинные
причины происходившего тогда.
Почему математики по целому
ряду причин не были озабочены проблематикой познания и выявления Истины, и
почему их вполне удовлетворял её формально-логический рассудочный суррогат – непротиворечивость?
Непротиворечивость есть
сугубо формальное качество формулируемое рассудком в его движении на опоры-реперы форм, принимаемых по тем
или иным причинам за базовые, так сказать, наиболее
общие, которые и становятся достаточным основанием самого указанного движения,
но основанием и движением формальным.
«Прекрасно
понимая, что от претензий математики на роль носительницы абсолютных истин о
реальном мире необходимо отказаться, критически мыслившие математики в то же
время отдавали должное колоссальным достижениям своей науки в механике,
акустике, гидродинамике, теории упругости, оптике, теории электромагнетизма, а
также во многих отраслях техники; они по достоинству оценивали исключительную
точность даваемых математикой предсказаний в этих областях. Математика сражалась под непобедимым
знаменем истины, но одерживать победы ей позволяла какая-то скрытая и даже
таинственная сила. Необычайная эффективность математических методов в естествознании, разумеется,
нуждалась в объяснении (гл.XV), но отрицать мощь математики как инструмента
познания и отмахиваться от нее не осмеливался никто. Без сомнения, эту мощь не
следовало подрывать, погружаясь в лабиринты логических трудностей и
противоречий. И хотя математики, поступившись строгими обоснованиями, нарушили
собственные принципы доказательности, в их намерения отнюдь не входило навсегда
оставлять математику на прагматической основе. На карту был поставлен престиж
математиков, ибо как иначе они могли провести грань, отделяющую их возвышенную
деятельность от прозаической работы инженеров и ремесленников?
И некоторые математики
вознамерились еще раз пройти по едва различимым следам прошлого, оставленным в
процессе бурного развития своей науки, и проложить надежные пути к тому, что
уже достигнуто. Свои усилия они решили прежде всего направить на построение
(или критическую перестройку) оснований математики.
Чтобы привести в порядок здание математики, требовались решительные и
крутые меры. К тому времени уже стало ясно, что не существует твердой почвы, на
которой можно было бы без опасений заложить фундамент математики: столь
надежная на первый взгляд опора на истину оказалась обманчивой. Но,
может быть, гигантское здание математики станет устойчивым, если под него подвести прочный фундамент
иного рода, представляющий собой полную систему четко сформулированных аксиом,
определений и явных доказательств всех результатов, сколь бы интуитивно
очевидными они ни казались? Основной акцент делался не на истинность
утверждений, а на их логическую совместимость, т. е. непротиворечивость. Теснейшая
зависимость между аксиомами и теоремами должна была придать устойчивость всему
зданию математики. Отдельные части этого здания оказались бы накрепко стянутыми
скрепами независимо от того, насколько прочно само оно опирается на землю.
Так колеблется под напором ветра гигантский небоскреб, оставаясь тем не менее
единой, цельной конструкцией от крыши до фундамента.
Математики начали с оснований математического анализа. Но поскольку
математический анализ предполагает использование арифметики вещественных чисел
и алгебры, не имевших обоснования, нелогичность такого шага станет более
очевидной, если обратиться к следующей аналогии. Представьте себе, что владелец
пятидесятиэтажного дома со множеством жильцов, битком набитого мебелью и
различной утварью, узнав о шаткости здания, решает перестроить его — и начинает
капитальный ремонт с двадцатого этажа!».
Итак,
необходимо обратить внимание на следующие важнейшие моменты логики развития
обоснования математического знания, или иначе говоря, логику самодвижения
математики в направлении своего достаточного и необходимого основания:
А) условия и
причины того, почему евклидова геометрия и теория чисел столь длительное время
вполне удовлетворялись своим антично-формальным основанием;
Б) каким образом в какой последовательности
именно отношение отвлеченных математических форм выявляло в достаточном
основании – через абстрактное формальное отношение этих форм – основание необходимое:
«Если учесть, как прекрасно начал
строить Евклид дедуктивную систему геометрии и теорию целых чисел, то
нелогичность истории математики естественно подводит нас к вопросу: почему
математики так много и так безуспешно пытались обосновать иррациональные,
отрицательные и комплексные числа, алгебру, дифференциальное и интегральное
исчисление, теорию функций вещественного и комплексного переменного, в то время
как евклидова геометрия и теория чисел возводилась на столь шатком основании, и
почему это никого не смущало? Ответ на этот вопрос частично уже известен (гл.
V): поскольку развивавшиеся Евклидом разделы математики затрагивали интуитивно
совершенно ясные понятия (как точка или целое положительное число), найти
фундаментальные принципы, или аксиомы, из которых надлежало выводить остальные
свойства, было сравнительно просто, хотя аксиоматика Евклида вовсе не была
лишена недостатков и в ней отсутствовали как понятие неопределяемого объекта,
так и полноценные определения начальных понятий. Что же касается
иррациональных, отрицательных и комплексных чисел, операций над буквенными
символами, понятий дифференциального и интегрального исчисления, то они для
понимания гораздо труднее тех понятий, с которыми имели дело древние греки, и
поэтому некритическое их использование вызывает большую неудовлетворенность.
Но была и более глубокая причина. Сами того не желая, великие математики
вызвали своими трудами едва уловимое изменение в самой природе математики. До
XVI в. математические понятия были идеализациями или абстракциями, почерпнутыми
непосредственно из опыта. Правда, к тому времени отрицательные и иррациональные
числа уже были приняты индийцами и арабами. Но хотя мы отнюдь не склонны
недооценивать вклада, внесенного арабами и индийцами в развитие математики, в
вопросах обоснования они полагались главным образом на интуицию и
«внематематический» опыт. Когда же появились комплексные числа, а также
алгебра, широко использующая буквенные коэффициенты, производные и интегралы,
главенствующее положение в математике заняли понятия, представляющие собой
абстракции более высокого ранга. Так, понятие производной, или мгновенной
скорости изменения величины, хотя оно и не лишено интуитивной основы (ибо
существует физическое понятие скорости), является весьма абстрактным.
Качественно оно имеет совсем иную природу, чем, например, понятие треугольника.
Аналогичным образом были обречены на провал все попытки математиков — еще не
осознавших, что все эти понятия не основаны непосредственно на опыте, а
являются абстракциями более высокой степени,— понять, что такое бесконечно
большие величины, которых так старательно избегали греки, бесконечно малые
величины, которые греки так искусно обходили, а также отрицательные и
комплексные числа.
Иначе говоря, математики
создавали понятия, а не черпали абстрактные идеи из реального мира. В поисках
источника математических идей математики стали обращаться не к ощущениям, а к
человеческому разуму.
По мере того как новые идеи оказывались все более полезными в приложениях, их
принимали — сначала недовольно, а потом с жадностью. Становясь привычными,
новые понятия отнюдь не становились более приемлемыми: привычка лишь рождала у
математиков некритичность и создавала ощущение естественности там, где этой
естественности на самом деле не было. Начиная с XVIII в. в математику входило
все больше далеких от непосредственного опыта, все более абстрактных понятий,
которые тем не менее принимались с все меньшими трудностями. […]
Не почувствовав изменения, происшедшего в характере новых понятий,
математики тем самым лишили себя возможности признать необходимость иной основы
для аксиоматического построения своей науки, чем самоочевидные истины.
Разумеется, новые понятия отличались от старых большей тонкостью, и заложить
надлежащий Аксиоматический фундамент, как мы теперь знаем, здесь было совсем не
так уж просто. […]
Напрашивается еще один вопрос: почему математики были так уверены в
своих результатах, хотя они прекрасно понимали (особенно в XVIII в.), что
основные понятия математического анализа сформулированы недостаточно ясно, а
доказательства неадекватны? Отчасти такая уверенность объясняется тем, что
многие математические результаты были подкреплены опытом и наблюдением. Мы уже
рассказывали (гл. II) о замечательных предсказаниях в астрономии, сделанных на
основе математических расчетов. Но математики XVII—XVIII вв. верили в
правильность своих результатов и еще по одной причине: они были убеждены в том,
что мир сотворен богом на основе математических принципов, а они призваны постепенно
раскрывать планы творца (гл. II). И хотя их открытия не носили общего
характера, математики считали эти открытия составными частями единой
основополагающей истины. Вера в то, что они открывают детали божественного
замысла и в конечном счете достигнут когда-нибудь «земли обетованной» и вечных
истин, поддерживала дух математиков XVII—XVIII вв., вселяла в них бодрость, а
плодотворные научные результаты были для них манной небесной, питавшей разум и
облегчавшей их тяготы.[…]
В конце XVIII в. математики осознали,
что созданная ими наука отнюдь не была тем образцом строгости, каким ее
считали. Вместо дедуктивных рассуждений в ней широко использовалась интуиция,
геометрическая наглядность, физические соображения, принципы, взятые «с
потолка» (например, принцип перманентности форм), а в качестве аргумента для
обоснования принимаемого обращались к метафизике.
Идеал логической структуры, несомненно, был выяснен и провозглашен
древними греками. Немногих математиков, задавшихся целью достичь его в
арифметике, алгебре и анализе, поддерживала вера, что по крайней мере в одном
весьма важном случае— в евклидовой геометрии — столь высокий идеал был
достигнут. А если кому-то удалось однажды взойти на Олимп, считали они, то не
исключено, что и другие сумеют покорить вершину. Эти математики и не
предполагали, что подведение строгого обоснования под всю существующую
математику окажется задачей несравненно более трудной и тонкой, чем можно было
представить в середине XIX в. Не могли они предвидеть и новых трудностей, которые
возникнут на их пути».
Вновь вспомним
Вейля:
«Как показал К. Гёдель, всегда найдутся конструктивно очевидные
арифметические суждения, не выводимые из аксиом, как бы вы их ни формулировали,
и в то же время аксиомы, безраздельно правящие всеми тонкостями конструктивной
бесконечности, выходят далеко за пределы того, что может быть подтверждено
опытом. Нас не удивляет, что фрагмент природы, взятый в своем феноменальном
изолированном бытии, бросает вызов нашему анализу с его незавершенностью и
неполнотой; именно ради
полноты, как мы видели, физика проецирует то, что дано, на то, что могло бы
быть. Но удивительно другое: конструкция, порожденная разумом, — последовательность
целых чисел, эта, — обретает аналогичную неясность и ущербность, если подходить
к ней с позиций аксиоматики. Но тем не менее это факт, отбрасывающий зыбкий отблеск на взаимосвязь
опыта и математики. Несмотря на проницательность критической мысли — а может
быть, благодаря ей — мы теперь гораздо меньше, чем наши предшественники,
уверены в тех глубинных устоях, на которых покоится математика»
А так же:
«Но одну решающую, хотя саму по себе и не
достаточную, характеристику процесса понимания я хотел бы подчеркнуть:
различные стороны предмета математического исследования мы подвергаем
естественному разделению, каждую сторону в отдельности осваиваем, исходя из
особого, сравнительно узкого и легко обозримого набора предположений и затем
возвращаемся к целому, подходящим образом объединяя частные результаты в
сложное единство. Последняя, синтетическая, часть процедуры
носит чисто механический характер»
Обратим внимание на то, что аналитическое понимание математических
действий и отношений охватывает и понимание, опять же сугубо рассудочное и формализованное синтеза, как некоей сугубо формальной процедуры,
призванной просто соединить ранее
разъятое в некоторую общность.
Аформальное же понимание напротив, непрерывно видя
формальность различия форм именуемых «анализом» и «синтезом», и признавая
законность существования обоих форм, тем не менее не разрушает континуальный поток
превращения (перехода) одного в другое, не отрывает их друг от друга,
наблюдая воочию их встречную обоснованность друг другом как единого бесконечного
спиралеподобного движение одного в другом.
Осуществим и продемонстрируем в качестве элементарного
примера процедуру вывода того, о чем
упоминает Вейль: «простейшую и самую прозрачную для конструктивного ума вещь» - последовательность
целых чисел, которая с формальных позиций, как указано, совершенно неподвластна
и недоступна аксиоматическому подходу.
Итак, на необходимом (и
достаточном) трансформальном основании покажем Логику вывода
последовательности целых чисел.
Но для этого, прежде отдадим себе отчет в том, что логика такого вывода должна
быть тождественная логике вывода числа вообще, т.е. полей рациональных,
иррациональных, трансцендентных и комплексных чисел, ибо иначе такая
логика не могла бы быть и называться Логикой Всеобщего – Единой,
Трансформальной Логикой. По этой причине нам естественно придётся вывести и
обосновать все
иные формы алгебраических чисел, продемонстрировав
при этом существенные прорехи и пустоты существующего математического
фундамента, в частности в области того, что называются гиперкомплексными
числами, или кватернионами и октонионами,
являющимися мертвыми, искусственными,
формализованными числовыми формами.
Всё есть, так или иначе, число. Если бы некоторой произвольной
форме материального мира нельзя было поставить в соответствие её абстрактное
или идеальное символическое, и в
частном математическом случае числовое выражение-отражение, то не существовало бы и самого мира противоположного миру
идеального, атомарной (элементарно-числовой) символической единицей которого является число.
Видимо настала пора проделать то, что в своё время не
было сделано, а именно обоснование чисел как многообразия форм единого
основания:
«… математический анализ предполагает
использование арифметики вещественных чисел и алгебры, не имевших обоснования, нелогичность такого шага станет более очевидной, если обратиться к
следующей аналогии. Представьте себе, что владелец пятидесятиэтажного дома со
множеством жильцов, битком набитого мебелью и различной утварью, узнав о
шаткости здания, решает перестроить его — и начинает капитальный ремонт с
двадцатого этажа».
И мы сейчас проделаем это, правда, ни в коей мере не претендуя на полноту,
но показав, так сказать, общее направление с раскрытием ряда существенных
частностей, ибо излагаемый материал носит преимущественно пропедевтический
(учебный) характер.
Начнём. Необходимым математическим основанием, как
случаем необходимого абсолютного основания является понятие «Абсолют».
Абсолютное – Всё и Ничто абсолютно единое и абсолютно
обособленное, самопорождающее само себя и само себя исключающее,
Единственное-Множественное-Что-Есть-Было-и-Будет…
И нужно видеть, что особенно важно для математики, оперирующей
преимущественно предельно, бесконечно
вырожденным качеством, качеством количества – Абсолютное Основание
Всего – включая и Само Основание не является ни конечным, ни бесконечным,
Оно не есть форма и не есть не-форма, не есть Ничто и не есть Нечто… Абсолютное
– абсолютно лишено любой определенности, включая и определенность, выражаемую
понятием «неопределенности»…
На деле в силу движения
отношения в поисках Абсолютного мы, так или иначе, должны выйти к тому, что
является Абсолютным Первомоментом Абсолютного Основания, который в Самом
Основании и для Самого Абсолютного Основания является основанием:
«Прежде всего загадочным является
первый момент. Он есть «нечто», которое
тождественно самому себе в «этом» и в
«ином». Каким образом оно может быть самотождественно
и что значит эта самотождественность? Мы уже знаем, что «нечто»
есть, прежде всего, отсутствие всякого
полагания. Оно есть до-полагание. Итак,
до-полагание, предшествующее полаганию («этому») и ино-полаганию («иному»), одинаково
присутствует и в том и в другом. Но если
«нечто» еще не положено, то тут
возникает весьма глубокое диалектическое обстояние, требующее полного разъяснения. Если «нечто»
не положено, то оно есть чистое «нечто», т. е.
лишено всякого фона, на котором оно было
бы положено. Если что- нибудь положено,
оно тем самым окружается инобытием, полагается
в том, что не есть оно само, т. е. в инобытии. Такое же «нечто», которое никак не положено,
не имеет никакого инобытия, не окружено
никаким инобытийным фоном. Но то, что не
имеет вокруг себя никакого инобытийного окружения, то ничем и не отличается ни от чего. И вот это-то неотличие и требует ясного
представления.
То, что ничем ни от чего не отличается, может ли быть вообще чем-нибудь!
Что-нибудь, если оно действительно что-нибудь,
всегда отличается от всего иного именно этим
самым признаком чего-нибудь. Раз нет ни от чего отличия, нет и самого «чего-нибудь», нет этого
самого «нечто», а есть «ничто». Это один
из самых фундаментальных и в то же время вполне
примитивных тезисов общей диалектики.
Нечто, никак не будучи положено, не имеет
никакого инобытия, от которого оно чем-нибудь отличалось бы, и, следовательно, не есть
что-нибудь, т. е. оно ничто. Или: одно, если оно ни от чего не отличается (т. е. если нет никакого иного, другого), есть
ничто.
Это ничто, однако, не есть полное и абсолютное отсутствие всякого бытия. Это есть
абсолютное отсутствие бытия для мысли, так как
мыслить — значит прежде всего различать,
а где нет различения, там нет мысли. По бытию же это ничто не только не есть абсолютное отсутствие всякого бытия, а,
наоборот, полное его присутствие,
настолько полное его присутствие, что оно охватывает собою и бытие («это»),
и инобытие («иное»), и настолько
охватывает их, что уже содержит у себя все, все полностью; и даже не остается ни одной
точки, которая бы в него не входила и от которой оно чем-нибудь отличалось бы. Отсюда ясно, что бытие не есть последнее основание действительности, равно как и знание
не есть это основание, ибо то и другое
предполагает различение. Различение же
не изначально, оно предполагает инобытие. То же, откуда происходит и бытие, и
инобытие, выше и бытия, и инобытия; и
оно есть такое бытие, которое выше
всяких различений и выше самой противоположности знания и бытия.
Однако эти вопросы далеко выходят за рамки настоящего исследования и
должны иметь свое место в общей диалектике.
Здесь же нас интересует только вопрос о неразличенности изначального «нечто» и
о тождестве его с «ничто». Отсюда
вытекает, что изучаемое нами «ничто-нечто», охватывая все, есть уже абсолютное тождество, не тождество в каком-то одном отношении, но
тождество во всех решительно отношениях, тождество абсолютное. Выше мы нашли, что «это» и «иное»
тождественны между собою в смысле «нечто» и различны по
своему нумерическому бытию. Следовательно, получается, что «это» и «иное», с одной стороны, суть вместе некое
единое абсолютное тождество, с другой же
— оно некое абсолютное различие. Спрашивается: как совмещается между собою то и другое, абсолютное тождество и
абсолютное различие?
В «этом» есть некое бытие, носящее смысл «нечто»; и в «ином» есть некое бытие, носящее смысл
«нечто». Тут два различных факта,
носящих один и тот же, самотождественный смысл, смысл «нечто». Мы и
говорим, что по факту «это» и «иное»
разное, а по смыслу — одно и то же. Однако
при более близком исследовании этот вопрос приходится решать совсем иначе. Если в каждой
из этих областей есть факт (бытие) и
смысл («нечто») и если факты эти —
разные, а смысл — один и тот же, то как же общаются между собою в каждой отдельной
области эти ее подчиненные моменты, факт
и смысл? Допустим, что между ними
абсолютно нет ничего общего. Тогда получится, что «это» и «иное», тождественные в
одном отношении и различные в другом, тем самым
расслояются на две разные области, не
имеющие ничего общего. Одна часть
«этого» тождественна с одной частью «иного», а другая [часть] «этого», абсолютно оторванная
от первой его части, различна с соответствующей
частью «иного». Получается, что для объяснения
диалектического взаимоотношения «этого»
и «иного» мы принуждены были рассечь
единую и цельную природу «этого» и совершенно утерять его единство. Следовательно,
если «это» действительно есть, то бытие
и смысл в нем не могут быть абсолютно
различны. В каком-то отношении они должны
быть и тождественны. Если мы теперь опять повторим то же рассуждение относительно
различных и тождественных моментов в
бытии и смысле «этого», отбрасывая то,
что в них различно, и оставляя то, в чем они тождественны, то трудность повторится
снова: надо будет признать, что или
«это» рассыпается на еще большее количество абсолютно взаимно
дискретных частей, или же между ними
существует тождество не в каком- нибудь
одном отношении, но во всех отношениях, какие только возможны, абсолютное тождество. Стало
быть, или уже с самого начала «это» и
«иное» тождественны во всех отношениях,
тождественны абсолютно (а не в каком- нибудь
одном отношении), или то и другое рассыпаются на бесчисленное множество абсолютно дискретных
друг в отношении друга частиц. «Это»
рассыпается в алогическую пыль — неизвестно чего. Итак, диалектика показывает,
что «это» и «иное» не только тождественны между собою в одном отношении (в
смысле «нечто») и различны в другом
отношении (в отношении нумерического факта, бытия), но что они также еще и тождественны
между собою абсолютно, тождественны не в
каком-то одном отношении, но во всех
отношениях, которые только возможны.
Это понятно просто еще и потому, что «это» и «иное» содержат в себе «нечто», т. е. не-полагаемый
смысл, а этот последний, по нашему
исследованию, как ни от чего не
отличающийся, охватывает собою абсолютно все и есть абсолютное тождество. Стало быть, уже
по одному такому условию «это» и «иное»
оказываются абсолютным тождеством.
Вот каково диалектическое значение этого первого момента, отмеченного нами в сфере понятия
числа. Тут совсем нет ничего
удивительного, если мы внимательно отнесемся к процессу счета, который мы
сейчас анализировали. В самом деле, все
числа натурального ряда являются некими
единицами, единичностями, невзирая ни на какую величину данного числа.
Двойка есть такая же единичность, как и
единица; тройка также есть нечто и,
значит, нечто одно, единичность; четверка опять есть нечто, нечто одно, единичность и т.
д. Словом, единица, единичность фигурирует
решительно во всяком числе, целом,
дробном, рациональном, иррациональном и пр.; и, как таковая, она
везде совершенно одна и та же, везде она
абсолютно самотождественна. И только благодаря такой самотождественной
единичности и держится натуральный ряд чисел. Без нее он рассыпался бы вдребезги и нельзя было бы сконструировать ни одного числа.
Конечно, это еще не все. Числа не только тождественны между собой, но
еще и различны между собой. Однако диалектическое исследование показывает, что
эта самотождественность так же необходима, как и саморазличие».
Понятие «абсолютное» включая, разумеется, и математическое
абсолютное, является скорее не понятием, а абсолютным символом-понятием, непостижимой и непредставимой формально-смысловой сингулярностью и не более.
Но удел непостижимого,
включая даже «абсолютно непостижимое» – становиться
постигнутым и потому …. Абсолютное, оставаясь Собой
в силу необходимости тождества Себя – Себе, становится относительным и тем самым формально (трансформально) переходит в свою противоположность, соотносясь с Собой и в процессе такого
соотношения и его форм раскрывается,
обретая смысл.
Абсолютно Немыслимое и замкнутое в Себе Самом, таким
образом осмысливается и раскрывается.
Но раскрывается не чему-то стороннему и внешнему (ничего
стороннего и внешнего нет), а раскрывается Себе Самому как бесконечности
взаимодействующих и единых в Сущности фокусов движения самоотражения (самодвижения отражения), высшие формы которого уже становятся узнаваемы и даже
отчасти понимаемы относительным абсолютным как
человеческая форма Абсолютного Сознания и именуются этим относительным абсолютным «сознанием».
Математическим символом, обозначающим (фиксирующим,
определяющим, раскрывающим) Абсолютное (Всеобщее) Основания является «0»
(ноль).
Математики не было бы без уравнения и функции.
Уравнение и
функция – формы математических понятий вида «единичное (особенное) есть общее
(всеобщее)».
Символ
общности (всеобщности) – «0» принято располагать с правой стороны
математического выражения, без него такое выражение полностью теряет свой
смысл.
Интересно, что математики очень редко задумываются над
тем, что именно означает приравнивание того или иного математического (символического) выражения нулю.
А что оно может означать, как ни ту или иную форму значимости некоторой
математической формы, которую принимает, которой обертывается всеобщее основание и тем самым математическое
(символическое) выражение становится определенным
и обретает некий смысл?
Уже знакомая нам «рупа – шунья», т.е. «форма –
пустота». Но ноль (нуль) разумеется, ни есть «пустота», а лишь обозначение того
«нечто-ничто», откуда все исходит и произрождается, и куда и к чему все
возвращается.
Символически. Математически.
«Какое число в математике соответствует этому понятию границы как
диалектического синтеза, если под тезисом понимать положительное число, а под антитезисом—
отрицательное? Таковым числом является нуль. Нуль есть тождество полагания или
утверждения и отрицания, диалектический синтез положительного и отрицательного
числа — в смысле границы, отделяющей положителъные числа от отрицательных, и в
смысле предела, одинаково и одновременно как относящегося к той и другой сфере,
так и не относящегося ни к той, ни к другой сфере, а представляющего совершенно
отдельную, самостоятельную и оригинальную категорию.
… нуль есть граница в математическом смысле — это банальная истина
элементарных школьных учебников. Но необходимо понимать это не только математически,
но и чисто логически, т. е. диалектически. В арифметике или геометрии нуль —
граница между положительными и отрицательными числами в чисто счетном смысле.
Кроме того, во всех подобных рассуждениях у математиков звучит всегда нотка
условности, необязательности. Утверждают, что просто условились так, чтобы
вправо от центра координат по линии х-ов отсчитывать положительные величины, а
[влево—] отрицательные, и что в самом центре координат значение х и у равно нулю.
В логике не может быть такой условности. Вовсе не условились так, что между
положительными и отрицательными числами лежит граница, именуемая нулем, но иначе
и быть не может. Наличие нуля как границы неизбежно и неотстранимо для мысли,
как только она начинает прикасаться к этому предмету. Само основание бытия таково, что между положительным и отрицательным
числом лежит нуль и что этот нуль и положителен, и отрицателен и в то же время
не положителен, и не отрицателен. Диалектика нуля заключается в синтезировании
этих двух сфер и, стало быть, в их четком разграничении. Он — устойчивый и
твердый синтез числа как бытия, факта, как положенного и, следовательно,
положительного числа и числа как небытия, инобытия, идеи как отрицаемого и,
следовательно, отрицательного числа».
Таким образом, ноль не просто некоторое число, т.е.– не просто некоторая числовая граница, но граница всех границ,
т.е совершенно непостижимая формальным умом всеобщая граница Пространства в границах,
в пределах которого находится всё, все числа, вся математика:
«Само
основание бытия таково, что между положительным и отрицательным числом лежит
нуль и что этот нуль и положителен, и отрицателен и в то же время не
положителен, и не отрицателен. Диалектика нуля заключается в синтезировании
этих двух сфер и, стало быть, в их четком разграничении. Он — устойчивый и
твердый синтез числа как бытия, факта, как положенного и, следовательно,
положительного числа и числа как небытия, инобытия, идеи».
Как нам уже известно, ноль познавательно распадается
на ряд своих форм: формальную, аформальную и трансформальную, последняя есть одновременно и причина и следствие первых двух.
Трансформальный ноль или Т-нуль есть результат и
источник движения и перехода друг в друга нуля формального (арифметического),
т.е. «точки» и аформального – бесконечной
прямой являющейся диалектической противоположностью точки.
Но бесконечное и конечное едины и являют собой
трансформу этих двух форм. Бесконечная прямая замкнута относительно самой себя
(на саму себя) и является бесконечно большим – бесконечно малого – точки, форма структуры которой не может быть не
идентична структуре формы своего иного – прямой, ибо является ей,
диалектически тождественная ей.
Таким образом, трансформальная логика формирования
(оформления – формального и аформального) математических объектов, которые
обычно вводятся в математику аксиоматически, требует наличия вечной неизменной
и универсально-всеобщей формы математического универсума – кольца.
Точка, таким образом, структурно есть бесконечно малая кольцевая форма математического универсума.
Математический универсум есть вместе с тем то или иное математическое пространство, порождаемое формами своей реализации.
В зависимости от выбора формы реализации универсума
«точка» может быть точкой, т.е.
рассматриваться как формальная точка – бесконечно малое и лишенное каких-либо
измерений, а может быть пространством бесконечной прямой. Но рассматриваемые
сейчас нами базовые математические формы математических объектов (точки и
прямой) не являются собственно действительно трансформальными, т.е.
всеобщими. Они – лишь общие.
Математическая трансформа – это … абсолютное, рефлексивное движение которого, являющееся очевидно
движением отношения порождает общее.
Его (трансформальное) по понятным и уже
описанным выше причинам довольно трудно описать, но мы всё же попытаемся.
Попытаемся, используя метод аналогии или подобия.
Ещё раз вспомним Г.Вейля:
«Пространство бесконечно не только в том смысле, что в нем не
имеется конца; оно
кроме того в любом своем месте бесконечно, так сказать, во-внутрь, и точка в
нем может быть определена лишь путем бесконечного и от раза к разу все точнее и
точнее фиксирующего ее процесса деления. Это представление
противоречит интуиции покоящегося и законченного в себе бытия пространства».
И здесь необходимо отдать себе полный отчет о сути противоречия того, что действительно «противоречит
интуиции покоящегося и законченного в себе бытия пространства», т.е. попробуем понять, что т.н.
«вещественные (действительные) числа» в действительной реальности являются первой, назовем её α-мнимой
формой выражения,
раскрытия того, что может быть названо истинным числом, абсолютным числом-символом, которое и
есть некоторый аспект Математического
Абсолютного.
Фактически мы продолжим линию мысли А.Ф.Лосева об
Абсолютном Математическом – Первоосновании, которую мы начали рассматривать
парой страниц ранее, но, по-видимому, такое рассмотрение должно быть предварено следующим замечанием.
Вызывает
живейшее недоумение то воистину прискорбное обстоятельство, что столь драгоценное научное наследие, переданное гениальным русским мыслителем-философом А.Ф.Лосевым России и русским,
фактически на текущий момент лежит без дела, являя этим уже не столько «немой
укор», но скорее даже чудовищного диаметра философское «бревно в глазу» всей
мировой философии, не замечать которого уже
просто неприлично для человека даже просто слегка интеллигентного, не
говоря уже о многочисленных легионах носителей всё же кое к чему обязывающего титула
философа.
Мы приводим далее
большой отрывок из работы «Диалектические основы математики», который просто и
элегантно раскрывает и демонстрирует настоящую тайну истинного основания математики, о которой, как легко было заметить, сами математики не раз упоминали как о terra incognita.
На деле исторически весьма немногие философские работы
заслуживают высокого и чрезвычайно редкостного звания гениальных. И речь не о той дешевой доморощенной «гениальности»,
которая рождается рынком, когда в
роли повитух выступают те разнообразнейшие формы своекорыстного интереса, за
которым всегда стоит некоторая социальная группа.
Речь о плодах
истинного духовного мыслетворчества, на которых будет вечно и нерушимо стоять мир человеческий.
«Основная диалектика понятия числа. Обследуя три первые момента, установленные
нами в понятии числа (§ 19), мы,
следовательно, находим такое положение
дела. Число есть полагание, акт смыслового полагания («это», «одно», «бытие»), требующий для себя инобытия («иное»), в сфере которого и
совершается это полагание, и все эти
полагания объединены одним неполагаемым актом в одно абсолютное тождество
(«нечто»). Однако это далеко еще не
может считаться формулой числа — уже по
одному тому, что здесь употреблены понятия «объединения» и «одного», являющиеся числовыми понятиями, так что опять-таки
получается частичная тавтология. Эта
формула должна быть уточнена. «Объединение»
само должно быть разъяснено диалектически. Следовательно, до сих пор мы установили только одно: число есть акт смыслового полагания,
требующий для себя инобытия, в сфере
которого и совершаются эти акты. Как же описать это до-полагаемое
«объединение», в котором совпадают все
отдельные акты полагания?
Что это объединение вытекает из
абсолютной самотождественности до-полагания, это мы уже
знаем. Однако такое объединение есть,
собственно говоря, не объединение многого, но абсолютная единичность, в которой
нет ничего не только многого, но и
вообще раздельного. Необходимо, стало
быть, это абсолютное самотождество, или абсолютную единичность,
как-нибудь приблизить к реальному натуральному ряду, не
уничтожая этой природы, конечно, и не
принимая ее. Такое приближение получается
тогда, когда мы попробуем объединить «это» (бытие) и «иное» (небытие) в новую структуру,
дать их диалектический синтез. Из
общей диалектики мы знаем, что бытие и
небытие синтезируются в становлении. В становлении есть и то, что именно становится,
и принцип небытия того, что становится
(поскольку в каждый новый момент
становление уже не то, чем оно было в предыдущий момент). Но становление дает
становящееся объединение «этого» и
«иного», т. е. дает некое постоянно нарастающее осуществление упомянутой
абсолютной единичности. В этом процессе,
в процессе становления, абсолютное
самотождество (абсолютная единичность) не остается недвижным, но бесконечно повторяется,
и тут мы уже вплотную подходим к
логической конструкции натурального ряда
чисел. Итак, объединение бытия и небытия совершается в числе через введение 1)
принципа абсолютной самотождественности смыслового полагания
и 2) принципа становления этой
абсолютной самотождественности. Но и это еще не все.
Если формулировать наблюдаемый здесь нами диалектический процесс во всей
логической последовательности, то мы получим такую схему:
I
СУПРА-АКТ
(число
на стадии тождественности всех чисел, перво-
полагание,
не различенное полагание, акт вообще)
II III
ИН-АКТ (акт
полагания) КОНТР-АКТ
(акт отрицания)
(дифференцированное полагание,
число на стадии внешней отличенности; первое проведение границ, отделяющих одни полагания от других,— внешне раздельный акт полагания)
IV
ИНФРА-АКТ
(становление
раздельных актов полагания: число на стадии неопределенного пробегания по
отдельным актам полагания, как бы по отдельным точкам, «единицам»; становящиеся
границы чисел; совокупность внешне раздельных актов полагания)
V
ИНТРА-ЭКСТРА-АКТ, СТАВШИЙ
АКТ
(остановившееся
расширение границы числа, впервые дающее возможность пересчитать «единицы» в
данных пределах; внутренняя расчлененность числа; внутренно раздельная, внутренно определенная совокупность внешне
раздельных актов полагания)
VI
ЭНЕРГИЙНЫЙ АКТ,
или ПОЛНОЕ ЧИСЛО
(разрешившаяся
смысловая заряженность и получающаяся от этого внутренне-внешняя насыщенность определенной
совокупности актов этими самыми актамиполагания; внутренно раздельная и определенная совокупность внешне раздельных
актов полагания, проявляющаяся и вовне, как такая же внутренно раздельная совокупность,
или конкретно-индивидуальное число).
Здесь мы имеем I) до-полагание (которое можно назвать супра-актом), т. е. такое «нечто»,
которое не положено, не предполагает никакого инобытия и, следовательно, ни от
чего не отличается, не содержит в себе самом
антитезы бытия-небытия (утверждения-отрицания) и объединяет в себе все
раздельное (ибо во всем содержится).
Этот супра-акт, переходя в самополагание, вступает во взаимоотношение с инобытием,
которому неоткуда, конечно, взяться,
кроме как из этого же супра-акта, и потому необходимо считать, что сам супра-акт из себя порождает свое инобытие.
Получается II—III) антитеза «этого» — «иного», полагания и не-полагания,
или, иначе, акта полагания и акта отрицания. Эти два акта уже связаны взаимно и
взаимно предполагаются. Это не супра-акт, который ничему не противоположен и потому ничего, кроме себя, не
предполагает. Взятые в отдельности, эти акты не составляют числа, но они входят в него с такой же
необходимостью, как и супра-акт.
Супра-акт осуществляет в
натуральном ряду чисел его как бы общую
субстанцию, ту единую и нераздельную плоскость,
на которой этот ряд развертывается. Супра-акт есть скрепа всего натурального
ряда и скрепа каждого отдельного числа, держа входящие в это число единицы в одной связке, как одну идеальную индивидуальность.
Супра-акт связывает и отдельные единицы, входящие в число, в одно индивидуальное число
и связывает все числа натурального ряда в один индивидуальный, определенным
образом построенный ряд чисел. Число
«десять» состоит из десяти единиц, но нельзя это «состоит» понимать внешне механически. Одна
единица не есть десять единиц, и другая
единица тоже не есть десять единиц, так
же третья, четвертая и т. д. Спрашивается: как же из нескольких единиц вдруг
появилось нечто совершенно новое и
небывалое, совершенно новое число— «десять»? Ясно, что это «десять» есть некая определенная
индивидуальность и в пределах десяти единиц она определяет собою все десять отдельных единиц, равномерно
и абсолютно одинаково присутствуя в каждой такой единице и тем самым объединяя их в нечто
совершенно неделимое и абсолютно индивидуальное — в число «десять». Точно так же абсолютное
самотождество супра-акта смыслового полагания делает впервые возможным существование и многих таких отдельных
единичностей, т. е. существование
натурального ряда чисел. Без такого перво-принципа
ни одно число, входящее в натуральный ряд, ни в каком отношении не было бы
соизмеримо ни с каким другим числом
этого ряда. Без этой абсолютной числовой
единичности натуральный ряд рассыпался бы на отдельные числа, несравниваемые одно с
другим, а числа — на отдельные единицы,
также одна с другой несравниваемые и абсолютно взаимно дискретные.
Противоположность утверждения и
отрицания, вырастающая на лоне супра-акта, развертывает этот супра-акт,
конкретизирует его, дает ему разумность и раздельность, превращает из
потенциального в реальный акт смыслового
полагания. Однако ясно и то, что такая противоположность
не может оставаться абсолютной, без
всякого примирения и воссоединения с изначальным супра-актом. Она примиряется в IV) новом
синтезе, который в отношении супра-акта оказывается уже развернутым синтезом и
который, как мы видели, именуется становлением
(его можно назвать также инфра-актом, поскольку здесь мы имеем ослабленное
полагание, полагание не раздельных и четких актов, но размытое, безразличное,
чисто становящееся полагание). В процессе становления утверждение и отрицание,
«это» и «иное», бытие и небытие вступают
во взаимосвязь и взаимоотношение. Само
становление обеспечивает собою рождаемость бесконечного натурального ряда чисел
из недр супра-акта, а эта взаимосвязь
утверждения и отрицания определяется вполне
специальной системой категорий, из каковой вытекает характер и каждого
отдельного члена натурального ряда чисел. Каждый отдельный член ряда, т. е.
каждое отдельное число, есть уже
остановившееся становление, или то, что
в диалектике называется ставшим. Это
то, что не раньше акта полагания, а
позже его, когда он синтезировался с
актом отрицания и сам в себе определился.
Этот пятый момент — V) момент ставшего в числе впервые делает возможным
превратить неопределенную совокупность
актов полагания в нечто оформленное и определенное.
Наличие акта полагания и отрицания, ин-акта
и контр-акта, ровно ничего не говорило нам ни о какой совокупности актов. Это была пустая и неопределенная возможность различать акты вообще. С переходом
в становление, в инфра-акт, мы превратили эту неопределенную возможность в некую реальность,
т. е. перешли к ряду раздельных
полаганий. Тут уже не просто возможность
реальных актов, но и самые акты. Однако, как ни реальны они и как ни отличаются они
друг от друга, самое становление этих
внешне взаимно различных актов совершенно ничего не говорит о них как об определенной совокупности, совершенно не
полагает никакой границы для целого ряда актов. Акты тут отличны один от другого, и их разделяют четкие
границы. Но ряд таких актов, совокупность этих актов, здесь еще не имеет определенной ограниченности, не отграничена от
всякой другой совокупности. А ведь число
есть прежде всего некая определенная
совокупность единиц; и если мы хотим дать логическую конструкцию числа, мы
должны дать прежде всего конструкцию
числа как некоей совокупности. Ставшее становление и есть принцип, отграничивающий одну совокупность от другой, ибо
оно есть остановившееся становление: мы совершали различные акты полагания, а потом вдруг остановились, не
пошли дальше, запретили себе дальнейшее
становление. И это положило границу
нашим полаганиям и впервые превратило неопределенный ряд полаганий в цельную,
определенную и замкнутую совокупность. Возможно ли число без этого? Конечно, нет. Число и есть прежде
всего некая замкнутая совокупность.
На этом, однако, не кончается диалектическая эволюция нерасчленимого,
перво-сущего супра-акта. В «ставшем»
содержится статика, которая отнюдь не характерна для числа в целом. Статический
момент в нем есть только один из моментов. Исходным моментом, и даже не моментом, а
рождающим, и притом вечно рождающим,
лоном является для числа супра-акт, который
объединяет в себе и эманирует из себя всю бесконечность разных чисел и даже
бесконечность этих бесконечностей.
Таковым же должно явиться и каждое отдельное
число, если оно действительно несет на себе печать своего происхождения из такого
первоисточника. К этому же ведет чисто
логическая — диалектическая — необходимость.
Если синтезом утверждения и отрицания явилось
становление, становящаяся граница, а эта становящаяся граница предполагает
нечто не-становящееся, т. е. ставшее, то
ставшее, чтобы получить для себя необходимое
диалектическое оформление, также должно противопоставить
себя тому, что его отрицает, с тем чтобы
потом вступить с этим последним в живой диалектический
синтез. Противоположно ставшему не-ставшее, но такое не-ставшее, которое не
просто свободно от всякого становления и ставшего (это было бы характерно для гораздо более ранних
категорий), но свободно только от самого факта становления, не от его смысла. Должна
быть такая категория, которая содержит в
себе и становление и ставшее, но — идейно, в форме чистого смысла, так что от данного бытия как
бы распространяется смысловая атмосфера его становления, оно как бы разрисовывается текучими, но
сущностными формами бытия, превращаясь в некую текучую сущность. Это и есть
то, что мы называем энергией, тем
внутренним содержанием смысла бытия,
которое, оставаясь чистым смыслом,
изливается вовне, являя внешне таинственную жизнь внутренних недр бытия.
В применении к числу этот VI) момент, энергийный момент,
сказывается очень ярко. Число есть совокупность единиц, четко разделенная
внутри себя и четко разделенная со
всякой другой совокупностью. Но мы тут не
только что-то построили и потом забыли о построенном. Мы еще и пользуемся этой
постройкой. Мало указать пределы для
актов полагания и тем ограничить полученную
совокупность извне и изнутри. Число есть то, что совершается в этих пределах, жизнь,
совершающаяся в этом организме. До сих пор мы построили только скелет числа. Замкнутая совокупность
раздельных единиц, являющаяся данным
числом, есть только скелет числа,
смысловой контур числа. Число есть конкретная индивидуальность актов полагания, в то время
как самые акты, в их становлении и в их
ставшести, есть только субстанция, голая
и бездушная телесность числа, материальная сделанность числа, а не его живой
лик и не его живые и жизненные функции.
Ставшее становление акта полагания должно начать функционировать как таковое, чтобы получилось настоящее число. Мы не только
тут находимся в процессе лепки из глины
какой-нибудь статуи, но мы уже ее вылепили, поставили на место, отошли несколько в сторону, чтобы обозреть ее в
целом, и вот тогда статуя действительно
становится для нас статуей. В
синтезированной совокупности десяти актов полагания мы должны найти внутреннюю и внешнюю жизнь, не только одну сконструированность как
таковую. Внутри эти единицы могут быть
бесконечное количество пробегаемы нашим умственным взором вперед и назад; мало того, этих единиц должно быть не десять,
а сколько угодно, вполне неисчислимое
количество, и они могут, кроме того, до
бесконечности приближаться одна к другой. Вовне эти единицы должны быть
способны к бесконечному увеличению в своем количестве и к бесконечным вариациям и комбинациям по форме своего
объединения. Иначе не будет и десятки.
Десятка—это то, что можно превратить и в
9, и в 11, и в любое число, любого вида и
любой величины. Вот это-то и значит, что число есть смысловая
энергия акта полагания.
Супра-акт сам по себе не создает
числа; полагание акта, равно как и
отрицание его, также не создает числа; то
же и становление, как и ставшее. Но, вступая в диалектическое взаимоотношение,
все эти моменты создают именно число, потому что только в их всецелой объединенности
заключается настоящая жизнь числа. Супра-акт осуществляется, полагает себя, окружаясь
инобытием, от которого он себя
отличает,— тут еще нет числа. Но вот, отличивши
себя от инобытия, от своего отрицания, он отождествляется с ним, вступает в единое и
цельное самотождество как в некую
смысловую эманацию жизни,— и здесь зарождается наконец число».
Итак, опираясь на представленный выше материал, а также и прежде всего на его глубокое самостоятельное
осмысление, которое безусловно потребует и должно потребовать серьёзной работы,
необходимо совершить следующий шаг: попробовать представить, уяснить и в конце концов
понять логику появления-рождения и развития числа как некоторой абсолютной абстрактной
символической формы, которая появляется в результате движения (оформления) содержания,
того истинного, аформального и трансформального (абсолютного) числа, о котором
мы говорили выше.
Вспомним для начала, что такое т.н. мнимое, или
комплексное число.
«Комплексные числа, — расширение множества вещественных чисел […],
обычно обозначается
 . Любое
комплексное число может быть представлено как формальная сумма x + iy, где x и
y — вещественные числа, i — мнимая единица.
. Любое
комплексное число может быть представлено как формальная сумма x + iy, где x и
y — вещественные числа, i — мнимая единица.
Комплексные числа образуют алгебраически замкнутое поле — это означает,
что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных
корней (основная теорема алгебры). Это одна из главных причин широкого
применения комплексных чисел в математических исследованиях. Кроме того,
применение комплексных чисел позволяет удобно и компактно сформулировать многие
математические модели, применяемые в математической физике и в естественных
науках — электротехнике, гидродинамике, картографии, квантовой механике, теории
колебаний и многих других».
Несмотря на очевидность и простоту выражения отношения
вещественных и комплексных чисел, логика этого отношения – это не очевидная и точно
не банальная логика для абсолютного большинства человеческих сознаний, в том
числе и математических.
Дабы ощутить это зададимся вопросами, на которые
пытались и продолжают пытаться и сейчас ответить математики: «Каков смысл
мнимых чисел? Как их можно и главное – нужно интерпретировать?»
Причем речь не
о так сказать собственно формально и абстрактно-математической,
а о чисто необходимо-логической интерпретации, такой, что становится непосредственно-наглядной
связь и отношение т.н. «вещественных» и т.н. «мнимых» чисел, как некоего
единого движения подчиненного единому закону.
Иными словами, мы должны выйти на необходимое
основание и выявить логику своего рода рассматриваемых числовых форм самообоснования
чисел, показав, как число своим
собственным действительным движением превращается из т.н. действительно-вещественного
в т.н. комплексное.
Известная интерпретация комплексных чисел как точек или
векторов на плоскости, т.е. интерпретаций
вида (a,b) и
соответствующих правил манипуляции с числовыми значениями этого искусственного
математического комплекса, являет собой
некую удовлетворяющую математиков математическую форму и не более.
Привычная форма действительного числа («a») и числа комплексного (a,b) или a + ib, где a и b — вещественные числа, i — т.н. мнимая единица,
представляющая собой с точки зрения обычных чисел нечто совершенно невразумительное, призрачное, и воистину мнимое – квадратный корень из «минус единицы»:
 .
.
Очевидность наличия прогрессии: линия – плоскость –
пространство… в связи с числовой определенностью числа, т.е. действительные числа – это числа так сказать «линейные», которые
определены на числовой прямой, комплексные – числа на плоскости («плоскостные
числа»), гиперкомплексные – «пространственные числа» себя не оправдало. А если
и оправдало, то с весьма существенным ущербом потери так сказать числовой идентичности, иначе и конкретно
говоря – умножение кватернионов некоммутативно.
«Коммутативная операция — это бинарная операция
 , обладающая
коммутативностью (от позднелат. commutativus — «меняющийся»), то есть
переместительностью:
, обладающая
коммутативностью (от позднелат. commutativus — «меняющийся»), то есть
переместительностью:
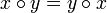 для любых элементов
для любых элементов
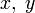 ».
».
Суть проблемы, если её видеть, в следующем:
«Почему, свободно манипулируя символами так, как если бы они были
натуральными числами, мы получаем верные результаты и в том случае, если вместо
символов подставляем вещественные или комплексные числа? Это происходит потому,
что вещественные и комплексные числа обладают такими же формальными свойствами,
что и натуральные числа. Если не гнаться за строгостью, то можно сказать, что
верно не только равенство 2•3=3•2,
но и равенство
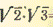
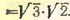
Иначе говоря, ab можно заменить на bа независимо от того, означают ли α и b натуральные или
иррациональные числа.
Весьма примечательна последовательность, в которой развивались события.
Вместо того, чтобы, начав с целых чисел и дробей, перейти к иррациональным и
комплексным числам, алгебре и математическому анализу, ученые решали проблему
обоснования математики в обратном порядке. Они действовали так, будто крайне
неохотно затрагивали проблемы, которые, как всем было ясно, можно было до поры
до времени обходить стороной, и принимались за обоснование лишь в тех случаях,
когда это вызывалось настоятельной необходимостью. Как бы то ни было, в 90-е
годы XIX в., через каких-нибудь шесть тысяч лет (!) после того, как египтяне и
вавилоняне «пустили в оборот» целые числа, дроби и иррациональные числа, математики
смогли наконец доказать, что 2+2=4. Стало ясно, что даже великие математики
должны заботиться о математической строгости».
Итак, для кватернионов в отличие от обычных чисел (действительных и
комплексных) «a» умножить на «b» не равно «b»
умножить на «a».
Создателем кватернионов был Гамильтон и именно он, к
слову, сделал первый шаг к формально-логическому обоснованию действительных и
комплексных чисел:
«Первый шаг к логическому
обоснованию вещественных и комплексных чисел был сделан в 1837 г. создателем
кватернионов Гамильтоном. Гамильтон знал, что комплексные числа можно
использовать для представления векторов на плоскости, и пытался найти (гл. IV)
числа с тремя единицами, которые могли бы служить представлением векторов в
пространстве. Гамильтон стал изучать свойства комплексных чисел с тем, чтобы
обобщить их. Одним из результатов, изложенных в его работе «Алгебраические
пары, с предварительным очерком о времени», было логическое обоснование
комплексных чисел, при построении которого Гамильтон, однако, считал свойства
вещественных чисел общеизвестными. Вместо комплексных чисел
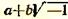 Гамильтон ввел упорядоченные пары (а, Ь)
вещественных чисел и определил операции над этими парами так, чтобы результаты
совпадали с результатами операций, производимых над комплексными числами
Гамильтон ввел упорядоченные пары (а, Ь)
вещественных чисел и определил операции над этими парами так, чтобы результаты
совпадали с результатами операций, производимых над комплексными числами
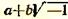 . Следует
заметить, что Гамильтону пришлось создавать новую теорию комплексных чисел,
поскольку для него, как и для всех его предшественников, были неприемлемы не
только символ
. Следует
заметить, что Гамильтону пришлось создавать новую теорию комплексных чисел,
поскольку для него, как и для всех его предшественников, были неприемлемы не
только символ
 , но до
какого-то времени и отрицательные числа. Позднее в одной из своих работ Гамильтон писал:
, но до
какого-то времени и отрицательные числа. Позднее в одной из своих работ Гамильтон писал:
Настоящая теория пар
опубликована, дабы продемонстрировать скрытый смысл [комплексных чисел] и
показать на этом примечательном примере, что выражения, которые все считали
чисто символическими и не допускавшими интерпретации, входят в мир идей,
обретая реальность и значимость,
Далее в той
же статье говорится следующее:
В теории
отдельных чисел символ
 лишен
всякого смысла [курсив Гамильтона] и означает невозможное извлечение корня,
или мнимое число, но в теории пар тот же символ
лишен
всякого смысла [курсив Гамильтона] и означает невозможное извлечение корня,
или мнимое число, но в теории пар тот же символ
 обретает смысл и означает возможное извлечение
корня, или вещественную пару, а именно (как мы только что убедились) главное
значение квадратного корня из пары ( — 1, 0). Следовательно, знак
обретает смысл и означает возможное извлечение
корня, или вещественную пару, а именно (как мы только что убедились) главное
значение квадратного корня из пары ( — 1, 0). Следовательно, знак
 может быть надлежащим образом использован во
второй теории, но отнюдь не в первой, и мы можем, если угодно, написать для
любой пары (α1, α2)
может быть надлежащим образом использован во
второй теории, но отнюдь не в первой, и мы можем, если угодно, написать для
любой пары (α1, α2)
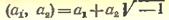
... и
интерпретировать символ
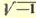 в том же выражении как обозначающий вторую
единицу, или чисто вторичную пару (0, 1).
в том же выражении как обозначающий вторую
единицу, или чисто вторичную пару (0, 1).
Так Гамильтон убрал то, что он назвал «метафизическими камнями
преткновения» в системе комплексных чисел.
В свою теорию пар Гамильтон включил и свойства вещественных чисел — пар
вида (а, 0). В работе от 1837 г. он попытался логически обосновать систему
вещественных чисел. Исходя из понятия времени, Гамильтон вывел свойства
положительных целых чисел, а затем распространил эти свойства на рациональные
(положительные и отрицательные целые числа и дроби) и иррациональные числа. Но
развитая Гамильтоном теория была логически весьма несовершенна и особенно несостоятельна
во всем, что касалось иррациональных чисел. Она была не только неясно изложена,
но и неверна. Математический мир вполне справедливо просто не заметил эту
работу Гамильтона. Интерес Гамильтона к обоснованию вещественных и комплексных
чисел был ограниченным. Истинной целью его исследований были кватернионы. Но
когда Гамильтону случалось работать в области математического анализа, он,
подобно большинству своих современников, без малейших колебаний свободно
оперировал свойствами вещественных и комплексных чисел».
Попробуем подойти к осознанию истинной числовой сущности
«мнимости», ответив на необычный, и кажется, не совсем математический вопрос: «В
каком направлении всегда и неизменно простирается
пространство мнимых чисел по отношению действительному числовому пространству?»
Иная, уточняющая и существенно снимающая патину
привычности восприятия пространства формулировка этого же вопроса: «В каком
направлении простирается четвертое измерение?»
«Патина привычности» – суть, как правило, не
осознаваемое сугубо формальное отношение пространственных форм, например, линейной и
плоскостной, как совершенно независимых и не сводимых друг к другу.
«Линия получается, является результатом движением
точки…»
«Плоскость является результатом движения линии…»
«Пространство – результат движения плоскости…»
Эти и подобные этим банальности, являющие собой
типичность сугубо формального видения
математических, в данном случае геометрических форм как раз скрывают и
отвлекают и не позволяют увидеть кое-что поистине удивительное.
Ответим, наконец, на поставленный выше вопрос: «В
каком направлении всегда и неизменно простирается пространство мнимых чисел в отношении числового пространства действительных чисел?»
Ответ скорее всего покажется странным. И к тому же
будучи услышан, будет не очень понятен, непонятен, скорее всего, настолько, что
последующие ряд страниц посвящены подробному рассмотрению смысла ответа,
ведь ответ: внутрь точки.
Отдадим также себе отчет в том, что чисто формальное,
и по сути отвлеченное и формально-аксиоматическое определение прямой, как
чего-то, являющегося движением «точки», или по-евклидовски, например, «не
имеющего толщины» или просто существующего как геометрический объект вида
«прямая» уже неявно предполагает существование некоего пространства, в
котором осуществляется такая геометрическая игра с готовыми и неименными и
видимо по этой причине неопределяемыми фундаментальными формами.
Эти формы известные уже более двух тысяч лет: «точка»,
«прямая» «плоскость», «окружность» и
т.д., которые обладают некоторыми свойствами или качествами, выводимые или
тоже являющиеся неопределяемыми,
например, «быть (существовать)», «быть параллельными», «пересекаться (иметь
общую точку)», «быть перпендикулярным», и пр..
Данность трехмерности, впитываемая человеком с первых часов его появления на свет, продолжает играть с
ним, если и не совсем и не всегда злую, то точно шутку.
Именно трехмерный мир и его формы становится познавательным основанием на котором и
выстраивается индивидуальное здание человеческого знания. И все такого рода
строения кажутся вполне надежными и даже достойными подражания или порой восхищения.
До некоторого момента.
Определенность прямой, трактуемая как её неопределенность и
аксиоматическая фундаментальность трактуется именно как некая абстрактная и
не требующая доказательства очевидность того,
что мы можем видеть буквально на каждом шагу в своей жизни. «Прямая» потому
является некоей абстрактной прямизной,
точнее идеей такой прямизны,
реальность которой нет необходимости как-то обосновывать.
И усвоенная каждым традиция формального обоснования
действенна и не дает осечек до момента, когда трехмерность становится уже недостаточным основанием, т.е. является основанием формальным.
Такое происходит и в случае, когда требуется внятно и однозначно указать направление т.н. четвертого измерения.
Перебрав в уме все мыслимые варианты, которые есть лишь многообразие комбинаций форм
представимого, человек, как правило, сдается или утверждает, что такого
направления просто не существует, или в
качестве своеобразного ухода от ответа утверждает, что такого направления – не
существует для нашего трехмерного
мира.
Существует и более того, логика рождения каждого
нового измерения одна, это логика
рефлексии единого необходимого основания, т.е. трансформальная логика,
логика единства, логика перехода
противоположного друг в друга через самого себя.
Представим кое-какую формальную аналогию, поясняющую в
каком направлении простирается
перпендикуляр, восстановленный к нашему трехмерному пространству.
Оттолкнемся от очевидного, то есть наглядного.
Пусть, например, вещественное число любого рода «а» как
точечная составляющая линейного континуума числовой оси раскрывается
относительно себя самого как абстрактной общей числовой формы в виде известного
представления т.н. комплексного числа: с=а+ib.
Иными словами вещественное
число есть комплексное число, мнимая часть которого равна нулю: b=0.
Обратим внимание, что мы
сейчас оперируем двумерным пространством, символическое формальное определение
которого включает в себя одномерное
в качестве своего предельного случая,
т.е. при стремлении вещественной переменной «b» к нулю (b→0)
комплексное числовое пространство становится вещественным.
Поскольку у нас есть в наличии предельный
переход, и область «мнимости» как сугубо комплексная область обладает
рядом интересных свойств, предположим, что эти свойства едины для всех
мнимых чисел любой мерности:
«…мнимая величина есть в диалектическом
смысле выразительная величина и что вещественная величина, перейдя в мнимость,
тем самым получает свое выражение, поскольку мнимость представляет собою
наличие в данном измерении перехода в следующее измерение без нарушения,
однако, прав первого измерения».
И ещё:
«… сколько бы измерений
мы ни брали, всегда, когда зайдет речь о переходе одного пространства на
другое, мы должны будем прибегать к помощи мнимых величин. Ясно: мнимая
величина есть отображение в данном вещественном измерении какого-нибудь другого
измерения. Данная вещественная величина получает здесь некое новое смысловое
оформление, получает внутреннюю перспективу, некий смысловой рисунок,
фигурность, не зависящую от того, что мы двигались внутри этой величины, ибо, пока мы были там внутри, мы не могли
видеть ее внешнего контура и фигуры и самое большое — это могли только двигаться
там в разных направлениях, т. е. устанавливать фигурность ее внутреннего
содержания, а не фигурность ее вообще. Теперь мы взяли эту внутреннюю
представленность величины, отошли от нее
на некоторое расстояние и тем самым наметили возможность зафиксировать эту
величину уже как таковую, со всей ее величии[н]ной фигурностью, на фоне
окружающей действительности. Взять внутреннюю представленность величины из
самой величины — это значит взять отрицательную единицу. Отойти от величины на некоторое расстояние, чтобы ее
видеть,— это значит отличить ее от того, что ее окружает, т. е. перейти в
отношении ее в сферу алогического становления, т. е. в новое измерение. И наконец, находясь в этом новом измерении,
обратить взоры на покинутую величину, с тем чтобы ее увидеть, т. е. с тем чтобы
определить тот исходный пункт, который лежит в основе самой ее
представленности,— это значит извлечь
квадратный корень из отрицательной единицы».
Пусть точка комплексной
плоскости совершает линейное движение изменением вещественной переменной в своей мнимой части:
с = a + bi, где b последовательно принимает действительные
значения из диапазона (0, 10).
Итак, точка перемещается в плоском комплексном
пространстве, двигаясь, как мы можем видеть, из своего двухмерного пространства – в его «глубину».
Изменяется ли при этом линейная вещественная координата?
По определению – нет.
Таким образом, точка,
обращаем внимание, одновременно принадлежа
(в рассматриваемом случае) двум пространствам – и линейному, и плоскостному
– движется, но… остается неподвижной, или если
переформулировать: «находится в данной точке и не находится в ней», причём, внимание! – даже в случае полной неподвижности относительно
«вещественного» линейного координатного пространства.
Относительно вещественного координатного основания, которое является одной из
форм-проекций комплексного плоского числового поля, точка неподвижна. Относительно мнимой оси,
также являющейся формой комплексного пространства – точка движется.
Казалось бы, на первый и
неискушенный взгляд имеется два несвязанных
и независимых друг от друга основания и таким образом классического
диалектического противоречия, в данном случае противоречия движения – нет.
Но так ли это?
Дело ведь как раз в том, в
каком смысле, как следует понимать «движение в комплексном плоском
пространстве».
Если «понимание», так и не
поднимаясь с уровня простого представления, то есть следует декартовской
формализующей традиции, и интерпретирует единое комплексное пространство лишь как форму двух независимых
линейных пространств, которые пересекаются под углом π/2 (прямым углом)
и точка пересечения является «началом координат», то никаких проблем с противоречивостью действительно нет, и нет именно
потому, что движение рассматривается относительно двух различных оснований,
т.е. единого отношения нет, есть различные
формальные отношения.
И, обратим также внимание,
что именно эти два формальных основания, которые и образуют т.н. «декартову
систему координат» являются причиной существования плоского числового поля, а
не наоборот.
Но первичным,
потому что единым является именно плоское пространство и точки
его образующие, и каждой точке может быть поставлена в соответствие некоторая
пара чисел, являющихся проекциями единой
координаты точки на числовые оси, первая из которых является т.н. «действительным»
числом, а вторая – «мнимым».
Эта методологическая
тонкость чрезвычайно важна, ибо позволяет видеть суть формализации,
расчленяющей единое на части и
рассматривающей затем полученные части в качестве двух различных и независимых
форм.
Но хотя формы-проекции и
есть, но они исходя из трансформ-логики вовсе не независимые, во-первых, а
во-вторых, именно их различие, а именно формальность различия – говорит об их
единстве!
Внимательно вдумываемся в то, что представлено далее.
Во-первых, все формы, как и их отличие друг от друга – мнимы, иллюзорны, и потому можно и нужно утверждать,
что они в своём роде ненастоящие – они в прямом смысле
лишь проекции, они тени истинного – и их ни в коем случае нельзя рассматривать как нечто самодостаточное и соответствующее
действительной реальности именуемой Истиной, которая едина для всех форм и является их источником и условием существования;
во-вторых, формы именно своей формальностью и относительностью
показывают и доказывают необходимость существования абсолютного, абсолютной формы всех форм;
в-третьих, форма Абсолютного не может не быть охваченным познающим субъектом пределом,
границей чего-то, что существуя как Целостность
Единства Бесконечномерного Пространства, в качестве своего необходимого основании
должна иметь своё противоположное – Множественность конечномерных пространств,
кажущихся полностью формально независимыми друг от друга.
Ум, воспринимающий некоторую
форму исключительно как лишенную внутреннего движения форму, ум, которому
недоступны тот или иной уровень мерности и соответственно качественности-всеобщности
познаваемого объекта или явления, ум не способный отразить в себе, представлять
и видеть в высших пространствах качеств в их взаимной связи и функциональном
отношении, который способен лишь фиксировать, как ему кажется независимые друг
от друга формы проекции, не понимая, что это проекции
единого, будет в лучшем случае утверждать простую и привычную формально-логическую противоречивость увиденного и помысленного
собой.
И такой ум является
носителем стандартно-формальных взглядов на предметы и явления мира, в котором
обитает.
Но к счастью известны, и как
ни странно хорошо известны единичные
примеры того как из форм-проекций можно собрать нечто единое и по этой причине истинное.
Семантический аспект такой сборки, то есть
оперирования в многомерности семантического
пространстве многим знаком в виде притчи о слоне и трех слепцах.
Трем слепцам которые никогда
не видели слонов и не знают, что они есть такое, дали возможность ощупать новый
для них предмет познания.
Одному достался хобот,
другому – уши, третьему – ноги. После этого у каждого спросили, что же такое
«слон».
Первый сказал, что «слон»
напоминает большую змею; второй утверждал, что «слон» это нечто плоское и
мягкое, а третий был уверен, что «слон» напоминает колонны…
Оказалось, что если
воспринимать и понимать каждую из проекций-форм «слона» как совершенно обособленные
и тем более единственные, то можно прийти к достаточно искаженному восприятию и
пониманию предмета…
Второй пример непосредственно
подходит и примыкает к понятию многомерности
некоторого целого и единого, но ограничивается его трехмерностью и
представляет противоречивость отношения «единое-множественное» в векторной форме, что вовсе не мешает сделать
соответствующие выводы и показывает, что математическая идея единого и его
форм, что называется давно и настойчиво «витает в воздухе», а если выразиться
точно «мыслеформа понимания формы некоторого единого как одной из его проекции
давно присутствует в ноосфере и улавливается самыми чуткими сознаниями».
Академик Б.В.
Раушенбах «Логика троичности».
Перед тем, как привести ряд
фрагментов из указанной статьи, несколько слов.
Мы, разумеется, не
утверждаем и не собираемся утверждать истинность христианской догмы о троичности
«Бога», как эту истинность понимают сами церковники.
Христос (Иисус из Назарета)
вовсе не был единственным «сыном божьим», были до Него, будут и после. Более
того, «божье сыновство» вовсе не является и не может являться качеством,
принадлежащим лишь Избранным
представителям Рода Человеческого. Миссия таких Представителей была бы совершенно
бессмысленной и провально, если бы те, ради кого они творили и страдали не были
бы уже сынами и дочерьми божьими – т.е. отпрысками, «детьми» Высшего, или, как ранее уже
было сказано, даже «детьми-богами», правда
ещё очень духовно неразумными по
причине своего младенчества-малолетства.
Итак, речь идёт просто о логике понимания «единого» как того, что
как мы уже знаем должно иметь своим необходимым
диалектическим основанием ряд своих форм-проекций, то есть быть «множественным». Таким образом, мы очень и
очень далеки от различного рода высказываний в отношении рассматриваемой нами
статьи, которые больше профанируют Великую Истину Единства Науки и Религии, чем
утверждают её:
«...Раушенбах, поднявшись туда, куда долететь можно лишь на крыльях ума,
души и духа, показал, что человеческое знание едино. Да нет, не показал –
математически доказал, что наука и религия описывают одну и ту же картину мира.
Его статья "Логика троичности", опубликованная в третьей книжке
"Вопросов философии" за 1993 год, сокрушила атеистическую догму, не
оставив камня на камне от "примата материи"».
Кроме того, статья весьма
интересна совокупностью поднимаемых и раскрываемых параллельно вопросов. Например,
вопросом о том, что истина необходимо обладает качеством антиномии
(демонстрируемой позицией о. Павла Флоренского). В качестве критики можно
сказать, что трактовка или интерпретация Раушенбахом взгляда П.Флоренского
можно считать довольно поверхностной.
Итак, "Логика троичности".
«Догмат о Пресвятой Троице является одним из центральных в христианстве.
Как известно, его становление было связано с борьбой различных богословских
точек зрения, в конце концов приведшей к единому мнению. Это мнение удалось
сформулировать в виде догмата, нашедшего свое выражение в никео-цареградском
Символе веры.[…]
Размышления о триединости вызвали целый поток недоумении, сомнений и
ересей. Человеческий ум всегда стремится понять высказываемое утверждение.
"Понять" означает включить это утверждение в совокупность истин,
подтверждаемых повседневной человеческой практикой, в конечном счете
согласовать его с рациональной формальной логикой. Кажущаяся несогласованность
догмата с формальной логикой толкала многих на еретические построения.
Здесь не место обсуждать возникавшие в течение столетий недоумения и
ереси, об этом можно узнать из истории Церкви. […]
Возвращаясь к Троице, можно сразу утверждать, что Лица в ней не просто
сосуществуют, а взаимодействуют — Сын и
Св. Дух связаны с Отцом рождением и исхождением, и уже поэтому элементарные
рассуждения Е.Н. Трубецкого могут оказаться ошибочными.
… будем искать в математике объект, обладающий всеми логическими
свойствами Троицы и если такой объект будет обнаружен, то этим самым будет
доказана возможность логической непротиворечивости структуры Троицы (отсутствие
в ней каких-либо антиномий) и в том случае, когда каждое Лицо считается Богом.
Это связано с тем, что вся математика построена на законах формальной логики.
Метод, который здесь будет использован, сводится, как видно из сказанного, к
доказательству изоморфности (обладания одинаковой логической структурой) Троицы
и некоторого математического объекта. Прежде чем приступить к этой операции,
надо четко сформулировать логические свойства Троицы. Они, безусловно, хорошо
известны, но здесь их необходимо сгруппировать вместе и уточнить.
1. Триединость. Это свойство совершенно очевидно, оно говорит о том, что
единый Бог и Троица одно и то же.
2. Единосущность. Здесь утверждается, что три Лица Троицы имеют
одинаковую Друг с Другом сущность. Иногда (об этом уже говорилось) эта сущность
определяется как Божеское достоинство. […]
3. Нераздельность. […]
4. Соприсносущность. Это свойство пришлось специально оговорить,
поскольку в погоне за тем, чтобы сделать догмат о Троице "понятным",
родилась ересь модализма. […]
5. Специфичность. Указанное свойство странным образом обычно не
подчеркивается, возможно потому, что кажется очевидным. Однако, анализируя
логику троичности, его следует сформулировать и обязательно учитывать при
поиске подходящего математического объекта, который еще предстоит провести.
Суть этого свойства сводится к тому, что, несмотря на единосущность, три Лица
не сводимы друг к другу, а каждое обладает своей спецификой. […]
Прекрасно понимая неуместность такого термина, рискну сказать, что
каждое Лицо Троицы выполняет свою "работу", не свойственную другим
Лицам.
При желании последние два свойства — соприсносущность и специфичность —
можно было бы объединить в одно: неслиянность (неслиянность Лиц и неслиянность
их действий). […]
6. Взаимодействие. Как уже говорилось, три Лица находятся в предвечном
взаимодействии, о котором нам известно лишь то, что сын рождается, а Св. Дух
исходит от Отца. […]
Математический объект, полностью
соответствующий перечисленным шести свойствам, действительно существует и
широко используется в математике, механике, физике и других аналогичных науках.
Это самый обычный вектор с его тремя ортогональными составляющими. Для
определенности будем считать этот конечный вектор имеющим начало в
ортогональной системе декартовых координат, а его составляющие направленными по
осям. Оценим, насколько точно его логические свойства соответствуют одноименным
свойствам Троицы.
1. Триединость. Она почти очевидна, поскольку сам вектор с одной стороны
и три его составляющие с другой — одно и то же. […] Для лиц, знакомых с
векторной алгеброй, особо хотелось бы подчеркнуть, что в приведенном
рассуждении не используется понятие векторной суммы; при определении
триединости это не нужно.
2. Единосущность — тоже почти очевидное свойство, поскольку три
составляющие вектора сами являются векторами. Полезно заметить, что никто и
никогда не говорил, что это обстоятельство ведет к антиномии.
3. Нераздельность. Каждая составляющая вектора связана с ним абсолютно,
поскольку является его векторной проекцией на соответствующую ось. Но тогда они
столь же абсолютно связаны и друг с другом, что и является нераздельностью.
4. Соприсносущность. Это тоже очевидное следствие того, что составляющие
вектора существуют всегда одновременно и вместе, иначе они не составили бы
систему векторов, в любой момент времени полностью эквивалентную исходному
вектору.
5. Специфичность … три составляющие вектора принципиально не способны
заменить друг друга, что и говорит об их специфичности.
6. Взаимодействие. Взаимодействие составляющих сводится к тому, что они
суммируются по правилам векторной алгебры. (В пункте 1 говорилось об
эквивалентности монады и триады, здесь же указывается процесс, ведущий к этой
эквивалентности.)
Как видно из проведенного анализа, логическая структура Троицы и вектора
с его тремя ортогональными составляющими полностью совпадает, что доказывает их
изоморфность. […]
У кого-либо может возникнуть впечатление, что векторная модель троичности
является еще одной из возможных иллюстраций триединства Бога. Это совершенно не
так. … это не модель Троицы, а лишь модель логической троичности, по зато это
не иллюстрация, а доказательство (что много больше).[…]
Во многих сочинениях, связанных с Троицей, в частности, в книге о. Павла
Флоренского, приводится ряд интересных мыслей о той роли, которую играют триады
в пашей жизни. Он приводит примеры пространства (три измерения), времени
(прошедшее, настоящее, будущее), указывает на то, что существует три грамматических
лица, что жизнь разума тоже троична (тезис, антитезис, синтез). Приводит о.
Павел и другие примеры11. Теперь к этому можно добавить, что особую роль в мире
играют не только триады, но и триединость, проявляющаяся буквально повсюду.»
И вновь, мы возвращаемся к ключевому в прямом
смысле - к математическому ключу к
диалектике, который просто и доступно раскрывает внутреннюю структуру
логики диалектического отношения: мышление являет собой и всегда имеет своим предметом многомерный объект, который
будучи собой и обладая качествами порождаемыми многомерностью, одновременно существует и как непрерывный комплекс форм себя во внутренних и внешних пространствах-проекциях.
Некоторая форма
всегда есть некоторая граница.
Некоторая форма
есть проекция, где «проекция» является обобщением понятия отношения.
Проекция пуста
и «отсутствует» лишь в случае полной, абсолютной прозрачности среды проецирования, прозрачности-однородности объекта
и субъекта производящего проецирование и также всех видов эманаций-форм первого
и второго, что утверждает их абсолютное единство и абсолютную безграничную, т.е. в пределе лишенную каких-либо границ
неразличимость.
И наконец, отсутствие каких-либо границ снимает все формы ограниченности
субъекта-объекта и делает его безграничным,
что и является определением Свободы.
«Единичное есть лишь единичное», «данная форма есть
данная форма», «точка это точка и более ничего», - утверждает формальное
мышление.
«Единичное есть общее»,
«Общее есть единичное» - утверждает знание
непосредственного трансформального видения.
Подведём важный итог нашим
рассуждениям цитатой из письма Георга Кантора и
её последующим транформальным анализом:
«Все так называемые доказательства
невозможности актуально бесконечных чисел являются,— как это можно показать в
каждом отдельном случае и заключить из общих соображений,— ошибочными по
существу и содержат
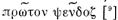 в том, что в них заранее приписывают или
скорее навязывают рассматриваемым числам все свойства конечных чисел. Между
тем, бесконечные числа, если только вообще их приходится мыслить в какой-нибудь
форме, ввиду своей противоположности конечным числам, должны образовывать
совершенно новый вид чисел, свойства которых зависят исключительно от природы
вещей и образуют предмет исследования, а не нашего произвола и наших
предрассудков.[…]
в том, что в них заранее приписывают или
скорее навязывают рассматриваемым числам все свойства конечных чисел. Между
тем, бесконечные числа, если только вообще их приходится мыслить в какой-нибудь
форме, ввиду своей противоположности конечным числам, должны образовывать
совершенно новый вид чисел, свойства которых зависят исключительно от природы
вещей и образуют предмет исследования, а не нашего произвола и наших
предрассудков.[…]
Если захотеть сгруппировать наглядным образом различные воззрения,
высказывавшиеся на протяжении истории по занимающему нас вопросу об актуально
бесконечном (которое в последующем обозначается для краткости через а. б.), то для
этого представляется несколько точек зрения, из которых ныне я остановлюсь на
одной.
А именно а. б. можно рассматривать в трех главных отношениях: во-первых,
поскольку оно имеет место in Deo extramundano aeterno omnipotenti sive natura
naturante и в этом случае оно называется абсолютным, во-вторых, поскольку оно
имеет место in concreto seu in natura naturata, и в этом случае я называю его
transfinitum; в-третьих, а. б. можно рассматривать in abstracto, т. е.
поскольку оно может быть постигнуто человеческим познанием в форме актуально
бесконечного, или, как я назвал это, в форме трансфинитных чисел, или в еще
более общей форме трансфинитных порядковых типов
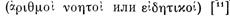 .
.
Если, прежде всего, мы оставим в стороне первую из этих проблем и
ограничимся двумя последними, то сами собой появляются четыре различные точки
зрения, которые фактически имели и имеют место в прошлом и настоящем. […]
Несмотря на существенное различие понятий
потенциальной и актуальной бесконечности,— причем первая означает переменную
конечную величину, растущую сверх всяких конечных границ, а последняя —
некоторое замкнутое в себе, постоянное, но лежащее по ту сторону всех конечных
величин количество,— к сожалению, слишком часто встречаются случаи смешения
этих понятий. Так, например, нередко встречающийся взгляд на дифференциалы как
на определенные бесконечно малые величины (тогда как они представляют собой
лишь переменные произвольно малые вспомогательные величины, совершенно
исчезающие из конечных результатов, а потому характеризовавшиеся уже Лейбницем
как простые фикции,— см., например, в издании Эрдмана, с 436) [17] основывается
на таком смешении. Но если из справедливой антипатии к подобному незаконному а.
б. в широких научных кругах под влиянием современного эпикурейски
материалистического духа времени образовался своего рода Horror Infiniti [18],
нашедший свое классическое выражение в упомянутом письме Гаусса, то связанное с
этим некритическое отвержение законного а. б. представляется мне немалым
преступлением против природы вещей, которые следует брать такими, каковы они в
действительности. Такое отношение можно рассматривать как своего рода
близорукость, которая лишает возможности видеть а. б., хотя последнее в своем
высшем, абсолютном носителе создало и сохраняет нас, а в своих вторичных трансфинитных
формах окружает нас со всех сторон и даже присуще самому нашему духу.
Часто происходит смешение другого рода, а
именно двух форм актуально бесконечного, причем смешивается трансфинитное с
абсолютным. Между тем эти понятия явно различны в том отношении, что первое
следует мыслить, конечно, бесконечным, но все же доступным дальнейшему
увеличению, тогда как последнее приходится считать недоступным увеличению, а
потому математически неопределимым. С этой ошибкой мы встречаемся, например, в случае пантеизма, и
она образует ахиллесову пяту этики
Спинозы, хотя Ф. Г. Якоби утверждал ее неопровержимость доводами разума. Можно также заметить, что со
времен Канта среди философов укрепилось
ложное представление, будто абсолютное является идеальным пределом конечного,
между тем как в действительности этот
предел можно мыслить лишь как некое трансфинитное и притом как минимум всех трансфинитов (соответствующий
наименьшему сверхконечному числу, обозначаемому мною через ω). Кант в
«Критике чистого разума» в главе об «Антиномиях чистого разума» оперирует без серьезной предварительной критической работы
понятием бесконечности при рассмотрении
четырех вопросов, стараясь доказать, что на них с одинаковым правом можно дать утвердительные и
отрицательные ответы L19]. Вряд ли
когда-либо — не исключая пирроновский и академический скепсис, с которым у Канта столь много
общего,— что-нибудь так способствовало дискредитации человеческого разума, как
этот раздел «критической трансцендентальной философии». При случае я покажу,
что лишь благодаря смутному
неотчетливому употреблению понятия бесконечности (если еще можно говорить о
понятиях при подобных обстоятельствах) этому автору удалось вызвать серьезное
отношение к его антиномиям и к тому же только у тех лиц, которые, подобно ему,
предпочитают уклоняться от основательного математического рассмотрения подобных вопросов [1].
[…] Точно так же я должен отклонить, как
неудачное, сопоставление с Гегелем. Пантеист Гегель не знает никаких
существенных различий в а. б. Для моих же воззрений характерны именно подобные
различия, которые я нашел, резко подчеркнул и строго математически развил
благодаря открытию коренной противоположности между «мощностью» и «порядковым
числом» множеств, что, по-видимому, совершенно проглядел г-н Вундт, хотя она
встречается почти на каждой странице моих работ. Столь же мало сходства имеют
мои исследования с «метаматематическими» исследованиями, с которыми их все же
ставит на одну доску г-н Вундт. Неустойчивость в определении понятий и
связанная с нею путаница, занесенная впервые около века тому назад с далекого
востока Германии в философию, нигде не обнаруживается столь ясно, как в
вопросах, относящихся к бесконечности: это ясно видно из бесчисленных как
критицистических, так и позитивистских, как психологических, так и
филологистических работ теперешней философской литературы».
Начнём с конца цитаты:
«Точно так
же я должен отклонить, как неудачное, сопоставление с Гегелем. Пантеист Гегель
не знает никаких существенных различий в а. б. Для моих же воззрений характерны
именно подобные различия, которые я нашел, резко подчеркнул и строго
математически развил благодаря открытию коренной противоположности между
«мощностью» и «порядковым числом» множеств…»
И здесь с Г.Кантором никак нельзя согласиться. «Пантеист» Гегель
знает бесконечное число различий в
«актуальной бесконечности», ибо понимает, что такое есть конечное, в
отличие от всех иных, для которых понятие бесконечное лишь формальная
абстракция.
«Единственное, к чему я вообще стремился и стремлюсь в своих философских
изысканиях, — это научное познание истины. Такое познание является наиболее
трудным путем, но только этот путь может представлять интерес и ценность для
духа, если этот последний, однажды вступив на путь мысли, не впал в суетность,
а сохранил неустрашимую волю к истине. Он вскоре находит, что только метод в
состоянии обуздывать мысль, вести ее к предмету и удерживать в нем.
Впоследствии обнаруживается, что такой методический путь сам есть не что иное,
как воспроизведение того абсолютного содержания, от которого мысль сначала
порывалась уйти и уходила; но это воспроизведение в глубочайшей, свободнейшей
стихии духа.[…]
Мнение, будто философия находится в антагонизме с осмысленным опытным
знанием, разумной действительностью права и простодушной религией и
благочестием, это мнение является скверным предрассудком. Философия признает
эти формы и даже дает им оправдание. Мыслящий ум не только не отвращается от их
содержания, а углубляется в него, учится и укрепляется на них, как и на созерцании
великих явлений природы, истории и искусства, ибо это богатое содержание,
поскольку оно мыслится, и есть сама спекулятивная идея. Коллизия между этими
формами и философией наступает только тогда, когда они выходят за свойственные
им пределы, облекают свое содержание в категории и делают содержание зависимым
от последних, не доводя их до понятия и не завершая их в идею.[…]
… идея спекулятивной философии принимается в ее абстрактной дефиниции,
причем либо полагают, что всякая дефиниция должна сама по себе выступать в
качестве ясной и завершенной и иметь свой критерий и пробный камень только в
заранее принятых представлениях, либо по меньшей мере не знают, что смысл,
равно как и необходимое доказательство дефиниций, содержится только в ее
развитии и в том, что она является результатом этого развития. Так как идея
есть вообще конкретное, духовное единство, а рассудок состоит в понимании
определений понятия лишь в их абстрактности и, следовательно, в их
односторонности и конечности, то это единство превращается представителями
рассудочного мышления в абстрактное пустое тождество, в тождество, в котором,
следовательно, не существует различия, а все есть одно и то же, в том числе
добро и зло. Название система тождества, или философия тождества, сделалось
поэтому общепринятым для обозначения спекулятивной философии».
Вспомним
ещё раз, что есть спекулятивная философия:
«Отсюда видно отношение спекулятивной науки к другим наукам. Она не
отбрасывает в сторону эмпирического содержания последних, а признает его, пользуется
им и делает его своим собственным содержанием: она также признает всеобщее в
этих науках, законы, роды и т. д., но она вводит в эти категории другие
категории и удерживает их. Различие, таким образом, состоит лишь в этом
изменении категорий. Спекулятивная логика содержит в себе предшествующую логику
и метафизику, сохраняет те же самые формы мысли, законы и предметы, но вместе с
тем развивает их дальше и преобразовывает их с помощью новых категорий.
Нужно различать между понятием в спекулятивном смысле и тем, что обычно
называют понятием. Тысячи и тысячи раз повторявшееся и превратившееся в
предрассудок утверждение, что бесконечное не может быть постигнуто посредством
понятия, имеет в виду понятие в последнем, одностороннем смысле.
Это философское мышление само нуждается в том, чтобы была понята его
необходимость и оправдана его способность познавать абсолютные предметы. Но
такое понимание и оправдание есть само по себе философское познание и поэтому
может иметь место лишь внутри философии».
Всякое конечное – бесконечно, являя собой форму-границу этого
бесконечного в его бесконечном переходе к абсолютному. И именно понимание,
спекулятивное, бесконечно-всеобщее понимание и рефлексия понимания своего
понимания позволяют непосредственно увидеть, что «самое-самое-самое» большое
число тоже является и не может не являться ничем иным как формой-границей своего рода чисел, которые закономерно вырастают из простого бесконечного числа, которое
уже не может быть никаким образом увеличено лишь по той простой причине, что
являет собой новое качество (ещё раз):
«Делая мысль своим предметом, я нахожусь у самого себя.
«Я», мышление, согласно этому, бесконечно, потому что оно в мышлении
соотносится с предметом, который есть оно само. Предмет вообще есть нечто
другое, нечто отрицательное по отношению ко мне. Но если мышление мыслит само
себя, то оно имеет предмет, который вместе с тем не есть предмет, т. е. имеет
снятый, идеальный (ideeller) предмет; мышление как таковое в своей чистоте не
имеет, следовательно, предела в себе. Конечным оно является лишь постольку,
поскольку оно останавливается на ограниченных определениях, которые признаются
им чем-то последним. Бесконечное,
или спекулятивное, мышление точно так же определяет, но, определяя,
ограничивая, оно снова снимает этот недостаток. Не следует подобно обычному
представлению понимать бесконечность как абстрактное выхождение за всякий вновь
возникающий предел, а следует понимать его тем простым способом, который мы
разъяснили выше».
Стоит со
всем вниманием сравнить данное определение
бесконечного (Ф.Гегеля) с тем, которое было дано Кантором, а сравнив увидеть и
понять, что вполне можно говорить об их полной тождественности в силу фундаментальной
рефлексивности обоих:
«Кантор определил бесконечное
множество как такое множество, которое можно поставить во взаимно-однозначное
соответствие со своим собственным (т. е. отличным от всего множества)
подмножеством»
Иными
словами, бесконечное осуществляется и существует тогда, когда, например, можно
установить взаимно однозначное
соответствие между рядом целых чисел и подмножеством - рядом четных чисел. Со здравой, т.е. формально-обыденной точки зрения четных чисел должно быть вдвое меньше чем целых:
«Каждому целому числу при этом соответствует ровно одно четное число
(равное удвоенному целому), а каждому четному числу соответствует ровно одно
целое число (равное половине четного). Следовательно, в каждом из двух
бесконечных множеств — множестве целых чисел и множестве четных чисел —
элементов столько же, сколько в другом множестве. Установленное соответствие
(то, что все множество целых чисел можно поставить во взаимно-однозначное
соответствие с частью этого множества) казалось неразумным предшественникам Кантора
и заставляло их отвергать все попытки рассмотрения бесконечных множеств. Но это
не испугало Кантора. С присущей ему проницательностью он понял, что бесконечные
множества могут подчиняться новым законам, не применимым к конечным
совокупностям или множествам, подобно тому как, например, кватернионы
подчиняются законам, не применимым к вещественным числам. И Кантор
определил бесконечное множество как такое множество, которое можно поставить во
взаимно-однозначное соответствие со своим собственным (т. е. отличным от всего
множества) подмножеством».
Таким образом, для бесконечных множеств формальная
логика оказывается неприменима, ибо для них, например, часть равна целому.
Неудивительно,
что такая логика не могла найти
поддержки и признания у многих именитых ученых,
которые в силу возникновения такого рода логических парадоксов поступали просто
– они отказывали актуальной бесконечности в праве на существования, считая
возможной лишь потенциальную бесконечность:
«Большинство математиков (Галилей, Лейбниц, Коши, Гаусс и другие)
отчетливо понимали различие между потенциально бесконечными и актуально
бесконечными множествами и исключали актуально бесконечные множества из
рассмотрения. Если им приходилось, например, говорить о множестве всех
рациональных чисел, то они отказывались приписывать этому множеству число — его
мощность. Декарт утверждал: «Бесконечность распознаваема, но не познаваема».
Гаусс писал в 1831 г. Шумахеру: «В математике бесконечную величину никогда
нельзя использовать как нечто окончательное; бесконечность — не более чем
façon de parle [манера выражаться], означающая предел, к которому
стремятся одни величины, когда другие бесконечно убывают».
Таким образом, введя актуально бесконечные множества, Кантор выступил
против традиционных представлений о бесконечности, разделяемых великими
математиками прошлого. Свою позицию Кантор пытался аргументировать ссылкой на
то, что потенциальная бесконечность в действительности зависит от логически
предшествующей ей актуальной бесконечности. Кантор указывал также на то, что
десятичные разложения иррациональных чисел, например числа
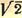 , представляют
собой актуально бесконечные множества, поскольку любой конечный отрезок такого
разложения дает лишь конечное приближение к иррациональному числу. Сознавая,
сколь резко он расходится во взглядах со своими предшественниками, Кантор с
горечью признался в 1883 г.: «Я оказался в своего рода оппозиции к общепринятым
взглядам на математическую бесконечность и к нередко отстаиваемым суждениям о
природе числа».
, представляют
собой актуально бесконечные множества, поскольку любой конечный отрезок такого
разложения дает лишь конечное приближение к иррациональному числу. Сознавая,
сколь резко он расходится во взглядах со своими предшественниками, Кантор с
горечью признался в 1883 г.: «Я оказался в своего рода оппозиции к общепринятым
взглядам на математическую бесконечность и к нередко отстаиваемым суждениям о
природе числа».
В 1873 г. Кантор не только занялся изучением бесконечных множеств как
«готовых» (т.е. реально существующих) сущностей, но и поставил задачу
классифицировать актуально бесконечные множества ([15]*, [53]). Введенные Кантором
определения позволяли сравнивать два актуально бесконечных множества и
устанавливать, содержат ли они одинаковое, «число элементов» или нет. Основная
идея Кантора сводилась к установлению взаимно-однозначного соответствия между
множествами».
Но актуальная бесконечность – это простая реальность математики:
«Классическим
примером актуально бесконечного множества по К. являются десятичные разложения
иррациональных чисел, т.к. каждый "конечный отрезок такого разложения дает
лишь конечное приближение к иррациональному числу". К 1873 относится
начало исследований К. по классификации актуально бесконечных множеств. Немного
позднее К. определил бесконечное множество как множество, для которого
существует взаимно однозначное соответствие с его собственным подмножеством
(т.е. отличным от всего множества). Одним из следствий такого подхода стала,
например, возможность установления взаимно однозначного соответствия между
точками прямой линии и точками многообразия любой размерности. Основываясь на
собственном определении бесконечных множеств, К. смог установить для каждой
пары из них отношение эквивалентности (равномощности). В 1874 К. доказал
несчетность множества всех действительных чисел, установив при этом
существование пар бесконечных множеств, имеющих различные мощности
(неэквивалентных множеств). Систематически основы своей теории математической
бесконечности К. изложил в 1879—1884. Основанием иерархии бесконечностей К.
стала доказанная в первой половине 1890-х широко известная теорема
К.-Бернштейна: "если два множества А и В таковы, что существует взаимно однозначное
соответствие между множеством А и подмножеством множества В и между множеством
В и подмножеством множества А, то возможно установить также и взаимно
однозначное соответствие между множеством А и множеством В", т.е.
установить равномощность (эквивалентность) множеств А и В. При этом, К.
определял, что если множество А возможно поставить во взаимно однозначное
соответствие с собственным подмножеством В, а множество В невозможно поставить
во взаимно однозначное соответствие с собственным подмножеством А, то множество
В по определению больше множества А. По мнению М.Клайна, такое определение
обобщает на случай бесконечных множеств то, что "непосредственно очевидно
в случае конечных множеств". Следуя данному подходу, К. доказал, что для
любого "заданного множества всегда найдется множество, большее
исходного" (например, множество всех подмножеств данного множества больше
первоначального множества). То, что между двумя мощностями возможно
установление отношений "равенство", "больше" и
"меньше", дало К. основание назвать "числами" символы
обозначения мощностей бесконечных множеств (для конечных множеств символы
обозначения их мощности суть числа натурального ряда, определяющие количество
элементов в каждом из эквивалентных конечных множеств). В отличие от чисел
натурального ряда [ординальных чисел /от нем. Die Ordinalzahl (Ordnungzahl) —
числительные порядковые — C.C.I, К. назвал кардинальными числами (от нем. Die
Kardinalzahl — числительные количественные)] "числа" обозначения
мощности бесконечных множеств. К. считал, что область определенных величин не
исчерпывается конечными величинами, т.к. об "актуальном бесконечном также
возможно доказательное знание". Если понятие мощности было расширенным
понятием "количество" для бесконечных множеств, то понятие кардинального
числа стало расширенным обобщением понятия "числа вообще". Расширение
К. понятия "числа" в область Бесконечного ознаменовало переход
математики на качественно новый уровень мышления. Фактически, мощность множеств
по К. отражает в сознании человека-исследователя определенные отношения
множеств, т.е. мощность множеств по К. — это наиболее общая характеристика
эквивалентных бесконечных множеств. Больцано еще в начале 19 в. пришел к
понятию взаимно однозначного соответствия между множествами (а, следовательно,
и к понятию мощностей множеств и выражению их кардинальными числами)».
Итак, ещё раз: ««самое-самое-самое» большое число
тоже является и не может не являться ничем иным как формой-границей нового рода чисел, которые закономерно вырастают из простого бесконечного числа, которое
уже не может быть никаким образом увеличено лишь по той простой причине, что являет собой новое качество».
«По нашей основной таблице типов числа мнимая величина должна явиться,
между прочим, диалектическим синтезом
нуля и бесконечности. Этот вопрос надо проанализировать по существу.
Нуль есть синтез положительного и
отрицательного числа, или, по общему правилу диалектического синтезирования,
граница между положительным и отрицательным числом; проведя границу вокруг положительного числа и
тем отличивши его от бесконечной стихии отрицательности, мы и получаем этот синтез — ограниченность положительного числа. Далее,
бесконечность есть диалектический синтез целого и дробного; это — граница между
тем и другим. Дробное — то, чем является целое в своем инобытии, если отнять
само целое и взять только инобытийные корреляты целого. Если теперь перенести в
это инобытие и само целое, то это целое окажется полной недостижимостью для тех
частей, из которых состоит инобытие целого, потому что инобытие есть всегда
неразделимость, а, подвергнутое счету, оно есть всегда неисчислимость. Потому
граница, отделяющая целое от дробного в этом диалектическом
синтезе, состоит из бесконечного количества точек; она есть, короче говоря, бесконечность.
Эти две границы, нуль и
бесконечность, находятся, несомненно, в положении диалектического противостояния. Нуль, отделяя положительные
числа от отрицательных, является только
одной точкой, рассекающей общую систему чисел; бесконечность же является целой
бесконечностью таких чисел. Это, конечно, есть диалектическая антитеза. Для уточнения можно сказать, что достаточно
уже только двух точек и достаточно, чтобы расстояние между этими точками было бесконечно мало, так как уже синтез
бесконечности (т. е. синтез целого и дробного) осуществляется, ибо между двумя элементами множества, как бы они близко ни были между
собой, всегда можно поместить еще одну точку. Это выражается в положении, что множество вещественных чисел повсюду плотно. Итак, каков синтез этих двух синтезов —
нуля и бесконечности и [какова] граница, совмещающая в себе обе эти границы —
границу в виде одной точки и границу в виде бесконечного количества точек?
b) Синтез должен
объединить в себе и тезис, и антитезис.
Другими словами, должна быть такая граница, которая есть и точка, и больше, чем
точка («больше, чем точка» — это, как сказано, уже есть бесконечное количество точек). Должна быть граница,
которая, оставаясь точкой, в то же время содержит в себе еще по крайней мере
одну точку, отличающуюся от другой; должны быть, следовательно, две точки,
которые являются в то же время [единством]. Что это значит и в чем тут дело?
Тут-то мы опять и должны призвать на помощь понятие числового контура, или числовой
образности. Когда мы имеем некое <...> А, оно остается неоформленным
вплоть до момента отличения его от не-А и отождествленным с самим собою. Только когда мы скажем «А есть А»,—
возможным делается оформление этого А и четкое отличие его от всего прочего.
Но, конструируя это содержание «А есть
А», мы как-то должны отличать А от А, т. е. от него же самого; иначе самое это
суждение «А есть А» окажется бессмысленным. Итак, А не только отличается от не-А, но отличается и от самого
себя,— это мы хорошо знаем из общей диалектики. Но из этой же общей диалектики
мы знаем, что это значит — отличие А от самого себя. Это значит то, что А есть
некое целое, имеющее части. Как целое оно отличается от себя как от состоящего
из частей (целое отличается от совокупности своих частей). Следовательно,
суждение «А есть А», в сущности, есть суждение «А как целое <…>, А как
совокупность частей». Но как раз это
самое мы утверждаем, когда отождествляем
границу в смысле нуля с границей в
смысле бесконечности.
Граница в смысле нуля есть последняя неделимая целость точки, та самая развернутая точка,
которая еще не имеет никаких частей. Такое целое мы в общей диалектике всегда и аналогизируем с неделимой
точкой. Граница же в смысле бесконечности есть совокупность некоей суммы
точек,— по крайней мере двух точек; тут — целое раздроблено, и раздробленные
точки объединены в некую сумму. Стало
быть, отождествляя (и, следовательно, синтезируя) границу-нуль с
границей-бесконечностью, мы попросту категориально
фиксируем границу-нуль, как бы говорим, что «граница-нуль есть
граница-нуль», т. е. как бы проводим эту границу-нуль жирной линией, делаем ее
твердой, абсолютно негибкой, создаем абсолютно крепкий контур, получаем эту самую границу границы, или форму границы, о
которой шла речь выше.
с) Итак, мнимое число есть также
диалектический синтез нуля и бесконечности.
[К] этому заметим, что в анализе понятия бесконечности мы сталкивались с одним недостаточным и неполным видом синтеза нуля и бесконечности,
именно с умножением нуля на
бесконечность. Это умножение дает неопределенную величину — как вещественную,
так и мнимую. Однако этот синтез, как мы там указали, неполный. Нуль и
бесконечность не функционируют тут как логические категории, но лишь как счетные величины. В то время как при диалектическом синтезировании обе категории входят в синтез
вполне равноправно и равномерно, при счетной операции умножения сомножители отнюдь не равноправны. Всякое
умножение имеет своей основной темой, главным своим предметом — множимое, и о
нем тут только и идет разговор; множитель же только показывает, что с множимым
творится в инобытийной сфере. Поэтому синтез [перемн]ожения — частичный, а
именно счетно-количественный, а синтез диалектический— полный равномерный, а именно логически-категориальный.
d) Наконец,
важно ощущать точную разницу между моментом числа ί, выражаемым при помощи
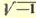 , и его
же моментом, выражаемым через синтез нуля и бесконечности. В первом случае в твердой оконтуренности и четкой смысловой фигурности, или образности,
числа выдвигается, как мы знаем, момент
полагания этой образности. Во втором
случае, поскольку речь идет о проведении самой границы, о ее, так сказать,
жирном черчении, нужно видеть противоположный момент образности, не субстанциальную ее положенность,
но ее очерченность, картинность, что,
несомненно, является чем-то противоположным первому случаю. Раз там субстанция числовой образности, то тут ее
идея. И нет ли теперь такого представления о мнимой величине, где она сразу
была бы дана и как субстанция числовой фигуры <...>, и как ее идея?»
, и его
же моментом, выражаемым через синтез нуля и бесконечности. В первом случае в твердой оконтуренности и четкой смысловой фигурности, или образности,
числа выдвигается, как мы знаем, момент
полагания этой образности. Во втором
случае, поскольку речь идет о проведении самой границы, о ее, так сказать,
жирном черчении, нужно видеть противоположный момент образности, не субстанциальную ее положенность,
но ее очерченность, картинность, что,
несомненно, является чем-то противоположным первому случаю. Раз там субстанция числовой образности, то тут ее
идея. И нет ли теперь такого представления о мнимой величине, где она сразу
была бы дана и как субстанция числовой фигуры <...>, и как ее идея?»
Таким образом, с учетов всего сказанного,
гипотетическое и несуществующее как полагает большинство математиков, математическое «наибольшее кардинальное
число», не может не быть банальным комплексным числом.
Количественность, неограниченно возрастая в бесконечности себя
и будучи взятая в качестве некоторого
целого и охваченного, становится
и не может не становиться качественностью.
«Наибольшее
кардинальное число» является при этом по существу своему лишь границей, которая одновременно и
разделяет, и соединяет линейную количественную значимость – с плоскостной, или т.н. действительные числа
– с т.н. комплексными.
Кардинальное
число есть, как выражается и, например, сам Бертран Рассел – «класс подобных классов», который всегда
больше, чем число предметов класса:
«Вы можете начать с вопроса,
существует или нет наибольшее кардинальное число. Каждый класс предметов,
которые вы можете выбрать для упоминания, имеет некоторое кардинальное число.
Последнее очень легко вытекает из определения кардинального числа как класса
подобных классов, и вы склонны предполагать, что класс всех предметов,
существующих в мире, имел бы столь много членов, сколько вообще разумно ожидать
от класса. Обыкновенный человек предполагал бы, что вы не в состоянии получить
класс больший, чем класс всех предметов, существующих в мире. С другой стороны,
очень легко доказать, что если вы возьмете выборки некоторых членов класса,
осуществляя эти выборки любым возможным для вас подходящим способом, число
различных выборок, которые вы сможете сделать, больше чем изначальное число
членов. Это легко видеть на примере с малыми числами. Предположим, у вас есть
класс как раз с тремя числами: а, b, с. Первая выборка, которую вы можете
сделать, - это выборка, не имеющая членов. Следующая выборка: отдельно а, отдельно b, отдельно с . Затем, bc, са, ab,
abc, в общем 8 (т.е. 23 )
выборок. Вообще говоря, если у вас есть n членов, вы можете получить 2n выборок. Очень легко доказать,
что 2n всегда больше чем n, будет ли n конечным или же нет.
Так вы находите, что общее число предметов в мире не является столь большим,
как число классов, которые можно получить из этих предметов. Я прошу, чтобы вы
принимали эти пропозиции как доказанные, поскольку нет времени переходить к
доказательствам, но все они имеются в работе Кантора*. Следовательно, вы
найдёте, что общее число предметов в мире никоим образом не является самым
большим числом. Наоборот, существует иерархия чисел больших, чем данное. На
первый взгляд, это, по-видимому, приводит вас к противоречию. Фактически, у вас
есть совершенно точное арифметическое доказательство того, что на небесах или
на земле имеется предметов меньше, чем
грезится нашей философии. Последнее демонстрирует
то, как философия делает успехи».
При этом известное
противоречие или парадокс, которое у нас получается в форме понятия «множества
всех множеств», которое одновременно должно
принадлежать и не принадлежать самому себе, есть лишь простое противоречие границы, которая также одновременно принадлежит
некоторому диапазону значений и не принадлежит ему, что демонстрируется
хотя бы дискретным числовым комплексом натурального ряда чисел: 1, 2, 3, 4, 5,
6, 7…, которым раскрывается логика линейной антиномии конечности-бесконечности.
Именно натуральный ряд воплощает в себе и
собой естественную законную спекулятивную противоречивость непрерывности и дискретности линейного числового континуума, в которой и которой раскрывается бесконечность.
При этом суть всех канторовских построений с совокупностью введенных им понятий весьма просто исчерпывается наглядностью и очевидностью того, что числовая прямая являет собой линейную
пространственную фрактальную структуру в которой, например, бесконечность единичного континуума точек (диапазона [0,
1]) есть подобие самой числовой прямой, опирающейся на бесконечный натуральный ряд чисел, но и порождающей этот ряд.
А с формально точки парадоксальным логическим завершением того, что не может быть завершено, и тем самым в
известном смысле является «абсолютным относительным» выражением
канторовской «абсолютной бесконечности» и является поле комплексных чисел, в котором
количество как простая одинарная
количественность как некоторое целое и единое обретает форму качества уже дуальной количественности, таким
образом продолжая начатое натуральным
рядом движение к Абсолютному Числу, которое (движение) есть одновременно движением от Абсолютного Числа и, оба движения есть единое
движение Самого Абсолютного Числа.
Здесь, по-видимому,
следует сказать (ещё раз) о том
основании, которое снимает как парадокс Кантора,
так и парадокс Рассела,
которые несомненно имеют единую природу – природу сущности границы, именно как понятийной
спекулятивной формы или формы-содержания, как
о-пределённой-предельной формы бесконечного рефлексивного движения содержания
во всём его объёме.
«Нужно различать между понятием в
спекулятивном смысле и тем, что обычно называют понятием. Тысячи и тысячи
раз повторявшееся и превратившееся в предрассудок утверждение, что бесконечное
не может быть постигнуто посредством понятия, имеет в виду понятие в последнем,
одностороннем смысле».
Что порождает указанные
т.н. парадоксы?
Только то, что
понятия, например, «конечное» и «бесконечное»,
будучи даже понимаемыми односторонне и формально, но в силу обстоятельств включенные
в бесконечность
последовательного рефлексивного формального отношения, которое последовательно,
исчерпывая формализм формального отношения форм, охватывает его как некоторую
целостность непременно ведёт к
парадоксам.
Таковы и
рассматриваемые нами рефлексивные понятия, которые осуществляются и существуют
как рефлексия
самих себя и этим оголяют, как правило,
укрытое в любом формальном формализме отношение противоречия.
Дело в том, что
даже простой однократный рефлексивный
акт движения-отношения от-себя-к-себе замыкаясь
мышлением в мышлении, образует потенциально и актуально бесконечный контур,
даже формальное повторение которого
раскрывает и строит истинную (антиномичную) содержательную структуру некоторого
формального понятия, и тем сближает противоположности бинера, всё точнее определяя одно противоположное
понятие через другое.
Так формально из
двух формальностей-противоположностей осуществляется строительство третьей.
Почему?
Отдадим себе
отчет в том, что речь идёт об отношении и связи не предельно простых и понятных
даже на уровне представления алгебраических чисел, являющих собой лишь начало,
старт бесконечного движения Абсолютного Числа, а понятий,
некоторых весьма и весьма сложных семантических
качеств, каждое из которых само по себе уже не может быть представленно в виде
простейшей линейной поляризованности
двух формальных противоположностей и формального нуля как их центра.
Иными словами,
понятие, являясь ничем иным как числом
или символом очень высокой меры развитости
значимости, многомерно по определению себя, скрывая в себе самом свою
противоположность как своё необходимое содержание.
Вспомним ещё раз,
что «мышление являет собой и всегда имеет своим предметом многомерный объект, который будучи собой и обладая качествами
порождаемыми многомерностью, в силу этого одновременно существует и как непрерывный комплекс форм себя во внутренних и внешних
пространствах-проекциях».
Противоречивость,
таким образом, на которую выходит математика в виде рассматриваемых нами и
многих иных парадоксов, есть простое противоречие форм-проекций сложного
многомерного понятия по отношению друг к другу, которые на уровне форм-проекций-пространств
рассматриваются вне связи друг с другом,
в качестве совершенно обособленных и независимых.
Итак,
на деле всё просто: если есть формальные противоположности, которые могут
рассматриваться и всегда рассматриваются формальным сознанием как независимые, то всегда существует и бинер, являющий собой единство этих
противоположностей; бинер и есть само поляризованное на противоположности спекулятивное
понятие, движение которого и воспринимается в качестве двух несвязанных
моментов противостоящих друг другу.
Вспомним далеко идущий вывод, который
делает Б.Рассел в работе, которой он пытается «спасти» теорию множеств от
противоречий, разрабатывая свою «теорию типов»:
«Фактически,
у вас есть совершенно точное арифметическое доказательство того, что на небесах
или на земле имеется предметов меньше, чем грезится нашей философии.
Последнее демонстрирует то, как философия делает успехи».
Человек, познавая мир,
строит многомерное пространство с всё более возрастающим числом границ. Каждое
понятие – становится границей,
которая как разделяет, так и связывает то, границей чего она является. На ранних этапах познания, этапах
познания-различения и познания-обособления понятие-граница, как правило, отделяет, разрывает, фрагментирует мир. Это и есть формальный
этап с господством формальной логики.
На позднем этапе, этапе
синтеза и сбора ранее разъятого и
обособленного, этапе который наступает уже после этапа формального различения мира те же понятия, которые служили
обособленно-несвязанными формами, понятия-границы-которые-разделяют становятся понятиями-границами-которые-соединяют.
Последние суть
спекулятивные, диалектические, аформальные и трансформальные понятия.
Итак, видя теперь любой
объект внимания и познания как объект многомерный, который скрывает формой свою
бесконечную глубину отдадим себе отчет в
том, что теперь у нас есть представимое и наглядное и по этой причине
становящееся вполне понятным математически
строгое истолкование диалектикой логики как логики отношений хорошо известных
математических форм одновременно отвечающих двум качествам:
1.
Эти формы независимо от внешней формальности формы бесконечны и многомерны;
2.
Все эти формы имеют единое абсолютное математическое основание из
которого вырастают и относительно которого определяются;
3.
Все эти формы порождены рефлексивным движением абсолютного
математического основания в-себе-самом-от-себя-к-себе .
Сформулированное знание как
раз и позволит нам подойти к решению интереснейшей проблемы построения общей теории чисел как Единого Числового
Пространства.
«Единичное есть особенное, единичное есть общее и
всеобщее», «данная форма есть и данная форма и нечто иное», «точка это точка, но точка есть и пространственная
форма внутри которой, в её внутреннем пространстве, поскольку
она является всеобщим – можно
обнаружить всё то, все те формы, которые может принять и
принимает всеобщее», - утверждает аформальное и трансформальное мышление и берёт в
качестве достаточного основания не ту или иную конечную форму или совокупность
форм, а трансформальную форму.
Обратим внимание на ту
очевидность, что при построении существующей теории чисел в качестве достаточного основания взяты вещественные числа, а в общем случае та
или иная сугубо формальная математическая форма, отвечающая «руководящему и направляющему»
принципу математической партийности –
«принципу непротиворечивости», что, как правило, и обусловило все трудности и противоречия,
с которыми сталкивалась и по сей момент продолжает сталкиваться математика.
Противоречивость – это фиксируемая формальным мышлением форма явления того, что некоторое математическое, символическое или семантическое «А» одновременно всегда есть и нечто иное, чем просто «А».
Итак, то что некоторая
определенность всегда есть неопределенность; что любое утверждение
и определение есть отрицание и буквально всё является становлением, далеко не сразу осваивается и усваивается познающим субъектом.
Лишь полное и успешное
прохождение необходимого этапа различения и анализа, в котором осуществляется формально-линейное координирование и
позиционирование познаваемого относительно-себя-самого-в-себе-самом, подводит
познающего субъекта к необходимости осмысления-понимания возникающего-рождающегося
из осмысления-представления.
Причем необходимо понимать, что представление есть лишь видимость отношения форм, т.е. ещё даже не собственно процесса отношения, но лишь возрастающей
в массе совокупностью финальных результатов
актов отношения.
Иначе говоря, тот или иной познаваемый
субъектом объект определяется в качестве семантической определенной формы, именно и строго как линейно
(иерархически-линейно) определенной относительно иных форм в линейном
пространстве, где под «линейностью» понимается простая параметрическая неизменность количественности (или параметрически
ранжируемой качественности) в границах области определения имени формы.
Объект представления (некоторая
определенная форма) есть конечная неизменная совокупность признаков (свойств),
где свойство (качество, признак) становится координатой, а именно линейной координатой общего линейного
иерархического пространства признаков. Лишь когда конечная неизменная количественная
совокупность становится неограниченно
возрастающей бесконечностью, охватываемой мышлением как некоторое целое, в ней способна родиться и
рождается новая качественность, являющаяся ничем иным как переходом от понятия-представления
об объекте к его понятию.
«Это» есть «это», «нечто
есть нечто», «А» есть «А», «количество есть количество», «качество есть
качество»… и т.д. действительно таковы – каковы они в своей формально-видимой определенности понимаемые как статичные независимые друг от друга формы.
Иными словами, формы в процессе аналитического
этапа познания позиционируются и определяются первоначально так сказать
евклидо-точечно, т.е. как лишенные структуры линейные и точечные образования,
где, например, координата такой не имеющей структуры «точки-формы» относительно
таких же «точек-форм» и есть сама определенная (определяемая) форма.
И если возникает
необходимость рассмотрения «внутренностей» некоторой формы, то пространство такой формы так
сказать «просто возникает» и
существует как точное подобие линейного пространства низшего или высшего уровня
иерархии, с полной их (рассматриваемых пространств) независимостью и отсутствием
связи друг с другом.
Итак, если сказать кратко,
то формальная логика – есть воображаемая и примитивная абстрактная логика
линейности и полной независимости познаваемых субъектом объектов познания в
линейном, т.е. как уже было отмечено ранее, своего рода, ньютоновском
пространстве, которое существует независимо от того, что в нём содержится.
Диалектическая логика
создаёт и оформляет пространство мысли, становящееся пространством
движения создаваемых субъектом форм мысли. Причем параметры пространства мысли
определяются (самоопределяются) как значения и значения-символы – количественные и качественные – разнообразных и
многомерных отношений форм мысли в процессе их (мыслей) самодвижения.
Из данного определения
становится вполне ясным, что транс-пространство мышления – нелинейно и более того – предельно
нелинейно, не говоря уже о том, что такое пространство бесконечно, точнее образует собой иерархию бесконечностей (в том
числе, разумеется и неколичественных),
кульминирующих в понятии «Абсолютного», являющегося началом-и-концом-всего,
включая и Себя.
Основа понимания: «Мышление являет собой и всегда имеет своим предметом многомерный объект, который будучи собой и обладая
качествами порождаемыми многомерностью, одновременно существует и как непрерывный комплекс форм себя во
внутренних и внешних пространствах-проекциях».
Иная формулировка того же: «нечто
– едино, но в силу этого, в силу внутренней противоречивости формы и того, что
сама эта форма есть форма всеобщего – множественно».
Или: «непрерывное – дискретно», или «общее – единично», или «качественность – количественна»
и т.д.…
Почему это происходит
вообще? А просто потому, что
необходимое всеобщее основание относительно которого мы определяем некоторую
форму не является формой, так же как и не является не-формой, и потому определяющим
направлением (в прямом смысле!) является направление порождающей связи отношения со
своим-иным, своим-противоположным.
Можно видеть, что математическая интерпретация философских
категорий общности и единичности (особенности) предельно ясна и наглядна – это отношение той или иной формы пространственности к форме своей проекции.
Например, отношение: «плоскость» (1) – «прямая» (2) – «точка» (3),
где 1 - («общее»), 2 - («особенное»),
3 - («единичное»).
Причем, «пространство», напомним
ещё раз, есть не что иное, как пространство самодвижения форм порождающих пространство
отношения форм, а не нечто абстрактное, некий отвлеченный «объем» существующий
независимо от живых самодвижущихся форм и как бы ожидающий наполнения ими.
Также можно видеть и
понимать, что остается открытым вопрос о том, как пространство n-измерений,
например n=1,2,3… превращается (переходит) в
пространственность n+1 и n–1 измерений, т.е. как
«точка» становится «прямой», а
«прямая» превращается в «плоскость», а «трехмерное пространство», например, становится
проекцией-плоскостью?
А действительно, как?
Напомним, что всё
представлено выше в объеме «нескольких страниц» являет собой, в том числе и пояснение смысла выражения «внутрь точки», т.е. «направления, в
котором n-мерное пространство, n=0,1,2,3…
становится пространством (n+1) измерений – это направление
вглубь (вовнутрь), или многократно использованное в тексте выражения «вхождение во внутреннее пространство точки (единичной формы)».
Итак, некоторая форма,
будучи собой формальным – или формой определяемой относительно всех иных форм,
играющих роль достаточного формального
основания и по этой причине рассматриваемая и
видимая и соответствующая рангу размерности определяющей формы (основанию определения), одновременно с
этим не исчерпываться этим формальным рангом определения, но простирается и ниже и выше его, ибо являет собой движение
развертывания (свертывания) самой формы
всеобщности.
Теперь, надеемся, уже можно
понять, или, по крайней мере, представить, что такое есть рассматриваемое нами математическое Всеобщее, наш
математический Абсолют, который поможет представить и понять Абсолют как таковой.
Математическое Абсолютное есть Абсолютное
Пространство, т.е. Пространство
Абсолютного Ранга, Абсолютно соотнесенное с Собой.
Не следует совершать ошибки понимания понятия «ранга»
как некоего чисто количественного параметра, пусть даже и бесконечного.
В некотором смысле «ранг» подобен понятию
«мощности» теории множеств Георга Кантора (своего рода «качественного»), но понятие
«мощность множества» всё же не выходит за границу количественной меры сравнения
бесконечных множеств. Та или иная форма
бесконечного, как количественного бесконечного способна породить и порождает различные качественные виды чисел (например, иррациональные, трансцендентные,
трансфинитные (кардинальные числа)), но все эти виды – это виды и меры количественности, виды и меры числовых
форм порождаемых линейным числовым пространством – действительной числовой осью,
и не более.
Как показано выше, Линейное
Бесконечное, взятое как целое и соотнесенное с собой и охваченное как единая форма, порождает из
самого себя качественно новый род чисел – плоскостную пространственность комплексного числового пространства, единичное
которого (точка комплексной плоскости) формально интерпретируется как
проекция числовых координат своих форм-проекций.
Мнимость числовая есть не что иное, как переход-становление-замыкания абсолютной
линейности на саму себя, рождение абсолютно-бесконечного числа, которое и можно
интерпретировать как своего рода «наибольшее число» числовой прямой.
Таким образом, тогда, когда часть и целое становятся
неразличимы и неотличимы друг от друга, т.е. прямая становится своей
противоположностью (бесконечных размеров замкнутым кольцом) количественность снимается, отрицается и превращается в новое качество, что, по-видимому, должно
быть довольно неожиданным для формального ума, который привычно совершенно
разрывает бинер «количество-качество» и все иные бинеры явленные числовой
прямой.
Итак, должно, быть понятным и совершенно ясным, что гипотетическое и с
точки зрения формального математического ума противоречивое канторовское т.н.
«наибольшее число», которое как число должно быть некоторой границей, действительно
является абсолютной-линейной-границей-самого-себя, такой границей, которая отделяет-соединяет линейное и плоскостное в единство бесконечного комплексного
пространства, являющимся следующим рангом
бесконечного вполне доступного математическому изучению и пониманию.
Комплексное число с = a + bi или (a,b) несравнимо
отдельно ни с (a), ни с (b), но сводимо к (a) в случае если (b)
устремить к нулю.
Тем самым, каждое новое измерение являет собой новую качественность, новый ранг качественности. Бесконечное
число измерений в совокупности и связи с количественной бесконечностью каждого
ранга, будучи соотнесенным с собой и опираясь в своём
самодвижении самоопределения на своё иное – на своё необходимое
основание порождает Абсолютный Ранг.
Итак,
Математическое Абсолютное есть Абсолютное Пространство, т.е. Пространство Абсолютного Ранга соотнесенное с Собой.
В свою очередь понятие
«соотнесения» просто предполагает реализацию трансформальной логики взаимного
порождения или опоры Абсолютного Основания на Самого Себя.
Довольно очевидным образом такого соотнесения является особое
качество присущее Абсолютному Движению, его относительный аналог и вполне
представимое подобие – вращение.
Движение Соотнесения Абсолютного Числа является Абсолютным Вращением
вокруг Центра, который собственно и есть Само Абсолютное Число.
Примеры.
Если вновь вспомнить о
некоей «Линейной Реализации Математического Абсолютного» (ЛРМА), о котором мы
уже подробно говорили и который подробно рассматривался нами ранее в предыдущих
главах, то этот, так сказать, «упрощенный», или скорее даже учебный вид абсолютного и демонстрирует сведённые к
некоторому пределу его качества.
Прежде всего, рассмотренный
нами учебный линейный абсолют (ЛРМА) не
выходит за границу количественности если рассматривать её в виде некоторой предельно простейшей (абстрактной) качественной формы.
Мы знаем, что математическим символом, обозначающим Абсолютное
(Всеобщее) Основания является «0» (ноль). Мы знаем, что ноль имеет ряд своих
форм.
Формальная форма (формальный ноль): «0».
Это арифметический ноль. Число-символ, смысл которого
– отрицание (формальное отсутствие количественного значения, формальное
отрицание) всякого числа-символа, кроме самого себя как символа формального отрицания.
Аформальный
ноль («Ò») – то есть «абсолютно всё иное, кроме «0»», формальное
отрицание которого есть «0». Содержательно – это вся
совокупность значений от –∞ до + ∞, исключая саму
точку «0».
Замыкание двух точек полубесконечностей в одну «равноудаленную»
бесконечно точку снимает как знаковую поляризацию, так и формальную
разомкнутость, порождаемую исключительно
формальным пониманием понятии «прямой», трансформальной порождающей основой
которой является её своё иное (противоположное,
т.е. «некоторая замкнутая кривая»).
Трансформальный ноль (T-нуль) – рефлексивное отношение (или всеобщая форма формы отношения) формального
и аформального нулей: «0//Ò».
Как известно отношение «0/Ò», взятое как абстрактно-всеобщее аформальное значимое (т.е. количественное значимое), есть простое
всеобщее отсутствие какой-либо
количественной значимости, то есть особое
числовое количественное качество т.н. «неопределенности».
Необходимым всеобщим основанием отсутствия
значимости («неопределенности») очевидно, является её столь же всеобщее наличие, т.е. определенность, и не просто определенность, а определенность всеобщая,
в свою очередь континуум (непрерывность) указанного отношения должен иметь
своим основанием квантованность (дискретность), являющуюся ничем иным как многообразием числовых форм.
Таким образом, мы получили и можем взглянуть на знакомую картину числовой прямой, но увидеть её несколько
иначе, уже не формально, и даже не аформально, но уже трансформально или в
самодвижении встречного порождения.
И прежде чем
изобразить всем известное изображение, за которым, и главное - в котором читателю предстоит увидеть
нечто такое, что совершенно не укладывается в формальное разумение самых умных
и знающих людей, посвятивших изучению математической сферы свои жизни,
несколько вводных слов.
Известное всем выражение «пересмотр основ» очень легко и просто произнести, но на
деле невероятно
сложно осмыслить, ибо осмысление предполагает выход за пределы
представления и переход к понятийному
видению.
Трансформа – не представима в принципе, хотя мы и
изыскиваем такие представления-формы и показываем их – рассказывая об их понятийном, то есть как бы скрытом в их глубине, или напротив, находящимся как бы вне их смысле.
Итак, ниже приведены два графических изображения,
своего рода стереопара того, что предстоит увидеть ментально.
Требуется совместить в неразрывное единство – т.е. ментально увидеть одновременно – оба
изображения и наконец уже свободно лицезреть ту познавательную глубину, которая не была ранее доступна.
Фигура 1 показывает нечто, хотя и в известном смысле условное, но достаточно точно (хотя
и абстрактно) передающее предельно противоречивый и антиномичный смысл абсолютного: «точка которая не
является точкой, в пространстве, не являющимся пространством».
•
Фиг.
1 Трансформа ЛРМА («Линейная Реализации Математического Абсолютного».
«не-Точка-в-не-Пространстве»
На фигуре 2 можно видеть знакомую картину обычной
бесконечной числовой прямой, которая является формой реализации Трансформы ЛРМА.

Фиг. 2 Числовая Форма Трансформы ЛРМА
Разумеется, Фиг.1 не является
действительным изображением трансформы,
но лишь некий отвлеченный образ-подобие того, что должно подтолкнуть ментальное воображение в необходимом
направлении.
Действительно, трудно
отразить некое трансформ-пространство, не являющееся собственно пространством,
в котором не имеет смысла понятие «величины» и «расстояния» и более того неприменимо
само понятие «формы»…
Например, это нечто не является чем-то конечным, но и
не является бесконечным, и в отношении его невозможно определить какое-либо
понятие границы, каково же оно это
нечто и как его изобразить, да к тому же на плоскости?
Вспомним основу диалектико-математического
понимания формы, пусть даже это и трансформа – любая форма многомерна, и в общем случае являет собой транс-форму абсолютного
ранга размерности.
Учитывая, что любое новое
измерение простирается как бы вовнутрь формы «войдем» в нашу трансформу двигаясь
вглубь её (Фигура.3а и 3б):

Фиг.3а Проникновение вглубь (внутрь)
пространства трансформы и тем самым определение
её (абстрактная линейная форма)
Фиг.3б Спиралеподобное движение
вглубь (внутрь) пространства трансформы и тем самым определение её – ей же самой (абстрактная рефлексивная форма)
И наконец завершающий кадр
ментального совмещения двух указанных ранее фигур, которые (или в которых) необходимо видеть одновременно, обе формы как единство (Фигура
4):
Фиг.4 Трансформа «0» и её α-поляризационная «внутренняя» мнимая форма определенности как её α-необходимое
основание
Абсолютно неопределимая и
неопределенная Трансформа ЛРМА («Линейная Реализации Математического Абсолютного» раскрывается (определяется) в форме (и как форма) внутреннего бесконечного
числового линейного пространства простирающегося во «внутреннем» пространстве
трансформы.
Итак, на фигуре 4 мы можем лицезреть «внутреннее»
бесконечное пространство трансформы, которая представлена на фигуре 1, причём
фигура 1. показывает то же пространство, но с видом «извне».
Причём, обращаем особое внимание, переход
от первого ко второму, как и от второго к первому осуществляется как особое движение,
то есть движение не относительно
некоторой формы и соответственно пространства этой формы, а относительно всеобщего
(бесконечного как целого), то есть в трансформальном направлении над- и под-
пространства.
Такое движение – это
движение абсолютного предельного перехода с охватом предела или трансформ-предельное
(т-предельное) движение.
Идёт ли речь о переходе во
внутреннее или внешнее пространство, т-предельный переход один и тот же.
Внутреннее пространство
фигуры 4 как бы свернуто внутри трансформы, но трансформа – это своего рода фрактал, растущий в самоё себя и потому подобный
процесс осуществляться бесконечно, что нами подробно рассмотрено в предыдущих
главах.
Но при этом ещё не было
сказано, что так сказать «по ту сторону» достигнутой и охваченной уже «внутренней» Абсолютной Бесконечности находится… бесконечность
«внешняя»,
та, с которой мы начали своё движение вниз по лестнице
иерархии определяющих форм - трансформа
и достаточно наглядного и обозримого ЛРМА, условно-учебного математического абсолюта.
Это и есть смысл используемого в предыдущих главах
выражения «выворачивания наизнанку» Абсолютного. В Абсолютном пространстве отсутствует понятие «внутреннего» и
«внешнего», а есть лишь непрерывный переход между ними, наглядным образом и
подобием которого для нашего трёхмерного пространства является односторонняя
поверхность кольца Мёбиуса.
Чем же наш учебный
математический абсолют отличается от настоящего?
Тем, что ранее
рассматривалась лишь его упрощенная линейно-аформальная модель, размерность
которой независимо от ранга размерности так и оставалась равной единице («бесконечное число колец вложенных одно в
другое»). Но это ни в какой мере не мешает такой модели линейного
математического абсолютного демонстрировать работу трансформальной логики.
Настоящий математический
абсолют как самодвижущееся (развертывающее и определяющее само себя математическое
Абсолютное Пространство (см. фиг.4)) во всём подобен действительному пространству, включая и ментальному, являя
собой его идеальную абстрактную числовую
(математическую) модель.
Здесь можно уловить ещё один
аспект, вероятно определяющий, смысла выражения «Всё есть Число».
Абсолют – лишь Символ «ВСЕГО-НИЧТО», включая и Саму
Себя порождающей и всё поглощающей Силы, используя введенные нами термины – трансформ-предельный и многомерный смысл и значение которой раскрываются
в знаково-числовых формах и их отношениях. Понятие «числа» как некоего
исключительно количественное значение чего-либо слишком формально и
ограниченно, чтобы отразить в себе бесконечность богатства форм бесконечного,
которое свернуто в пространствах,
которые в свою очередь находятся в формах разнообразных иерархий пространств.
Абсолютное по существу своему и есть Число.
Итак, математическое
линейное действительное числовое пространство в отношении абсолютного числового
пространства (абсолютного «А-числа») в действительности является – используя удачную, точнее по случаю ставшую таковой математическую
терминологию – мнимым.
Множество
действительных чисел является заявленной ранее первой α-мнимой формой выражения, раскрытия того, что может быть
названо истинным числом, абсолютным числом-символом или А-числом,
которое и есть некоторый познанный аспект Абсолютного являющий собой ту математику
которая сейчас известна.
Множество т.н. «комплексных
чисел», то есть чисел вида с = a + bi, где «а» т.н. действительная, а «b» -
т.н. мнимая часть комплексного числа,
а i – т.н. «мнимая единица», является следующей β-мнимой формой А-числа.
Таким образом учитывая всё
ранее сказанное, можно сделать ряд нетривиальных выводов относительно природы чисел и логики их порождения друг другом.
Вывод первый.
Мнимость числа (обычного
комплексного числа) есть просто признак или качество того, что математическое
выражение, включающее в себя комплексные значения или комплексную переменную
относится к внутреннему (т.е. мнимому) пространству находящемуся пространственно-геометрически внутри
его. Кроме того, очевидным и тоже уже не чисто количественным – качественным параметром этого
пространства является то, что это пространство большего и далее внутри
себя неограниченно возрастающего числа измерений.
Вывод второй.
Переход и своего рода
превращение действительного числа в число комплексное, осуществляется через
само действительное число, стандартной уже трансформальной процедурой предельного
перехода по
некоторому формально-выделенному параметру с его последующим охватом в качестве некоторого целого.
В данном случае этим
параметром является математическое понятие, которое можно определить как чистую простую количественность, то есть взятый
как целое, как предел неограниченный
беспредельный количественный рост действительного числа.
Поскольку мы находимся на таких
логических позициях, которые принципиально отрицают само наличие т.н. «дурной
бесконечности» как логической возможности,
во-первых, а во-вторых, предполагают естественный логический переход
противоположностей «количество - качество», то по всей видимости нет ничего
удивительного в том, что линейное пространство в своём развертывании порождает
в самом себе новое качество подобное качеству количественности, но уже двуликое.
Иными словами, из действительного
числового пространства как бы бесконечным
и неограниченным прорастанием его в самого себя, рождается комплексное пространство.
Рождается к слову, точно так же, как рождалось пространство самой
числовой прямой, но уже не линейной, а плоской поляризацией.
Обратим при этом внимание на
то, что картина (фигура 5) становится не просто подобной, но просто неотличимой, если рассматривать
(т.е. видеть, наблюдать) числовую прямую
в форме продольной «точечной» проекции, а вправо и влево распространяет
себя комплексное
числовое пространство, которое – будем об этом помнить – мнимо в той же мере, в какой является
мнимым (формальным или иллюзорным) пространство действительной числовой прямой,
которое мы видим сейчас в виде проекции точки «0».

Фиг.5 β-поляризация (плоскостная
поляризация) математического абсолюта (А-числа)
и рождение комплексных чисел комплексной плоскости
При этом конечно же необходимо
помнить, что в исходном, первом случае (фиг.1,2) воображаемая «точка»
математического абсолюта и не была точкой,
да и не имела вообще никакой формы и всех
атрибутов ей присущих, но рефлексивным движением (самодвижением)
абсолютного породило его соотнесенность с
собой и потому вызвало к жизни необходимую основу абсолютности - относительность.
Также легко можно догадаться, что,
соответственно – направление, в котором может быть осуществлено не развертывание (количественное
увеличение на единицу размерности), а свертывание (количественное уменьшение на
единицу размерности) числа пространственных измерений это выход во внешнее (относительно
рассматриваемой области пространства) пространство или движение определения из точки с её охватом.
Итак, должно стать понятным, что «качественность» в общем
случае является ничем иным как выявлением, неограниченным
движением раскрытия нового
количественного измерения.
Обратим при этом ещё раз внимание
на то, что раскрытие такого измерения в
некотором объекте осуществляется не извне, в изнутри его самого, его собственным
движением (самодвижением).
Такое раскрытие является формой самооформления необходимого
основания как его движения.
Итак, линейное пространство, например, в силу своего формального качества
(качества формы) – линейности, и
свертки всех иных качеств в указанной форме как своего необходимого основания искривлено, нелинейно и в общем случае замкнуто.
Линейное отношение пространственной нелинейности замкнутости прямой числовой оси
порождает – раскрывает сущность (основание) числа его новым формальным качеством, отныне такое число
уже как комплексное число характеризует пространство плоскости.
Понятно, что поле пространства
комплексных чисел, с = a + bi, где «а» т.н. действительная, а «b» -
т.н. мнимая часть комплексного числа,
ί – т.н. «мнимая единица», являющихся в нашем определении β-мнимой пространственной формой А-числа является необходимым аформальным основанием α-мнимой
формы А-числа.
Иными словами, α-мнимое
число есть частный случай, предельный переход или формальная проекция β-мнимого
числа.
Отсюда становится, вообще говоря,
совершенно ясным, что формальная
структура комплексного числа является универсальной структурой формы всей
противоположной Абсолютному А-числу или А-мнимой иерархии математических числовых
форм, т.е. α, β, γ, δ, ε, ζ…-мнимых чисел,
являющейся необходимым относительным основанием абсолютного А-числа.
Абсолютное раскрывается Относительным,
как и Относительное определяется Абсолютным в результате вечного перехода одного в другое…
… В Пространстве-не-являющимся-Пространством Пребывает
Извечно Точка-не-являющаяся-Точкой…
… Это –
Абсолют… Всё-во-Всём… Абсолютное Единое… Невыразимое…. Неразличимое… Абсолютно Лишенное
Формы и Границ… Абсолютно Недвижимое…Единственно-Реальное-и-Действительное,
Над-временное и Извечное…
… но
необходимо опирающееся, содержащее Бесконечно Глубоко-в-Себе Своё-Иное:
… Относительное, Не-Реальное, Мнимое,
Множественное, Подвижное погруженное в стихию Временности и Времени…
… Абсолютное - Лишь Абсолютный Неподвижный
Бесконечно Удаленный Центр Абсолютного Становления, который облекается в Своём Вечном
Движении-во-Времени к Центру Себя – Вечно Падая по Спирали в Свой Центр в
Стремлении достичь Его, но в Своём стремлении в Глубины Абсолютного Постигающего
и Достигающего и Строящего Непрерывно Его Внешние Границы, ибо Внешнее
Абсолютного – Глубоко Бесконечно Глубоко Внутри…
…Так
Центр-Абсолютное Вечно Перетекает в Глубину Себя Самого, Сливаясь и Обретая
Единство со Своим-Иным – Вечно Развертывающейся Раскрывающейся Периферией
Границ Абсолютного Становящегося Относительным и Относительным Превращающимся в
Абсолютное Через Самого Себя…
Абсолютное – Абсолютно
Тождественно Самому Себе, т.е. А = А.
Но такого рода
сверхтождественность, вне- и над-временная транстождественность может быть понята лишь через
противоположное тождества-единства, в котором совпадают и едины все
противоположности. Таким образом, Движение Познания и раскрытия того, что
противоположно Единству – познание Множественности и Различия, и составляет
оборотную сторону человеческого познания, но эта иная, противоположная,
полярная сторона находится в действительности по одну Сторону Абсолютного, ибо
у Абсолютного лишь Одна Сторона Одного Единого Движения Перехода
Противоположностей Друг в Друга Через Самих Себя.
И здесь мы обращаемся к Павлу Флоренскому, к его работе
«Мнимости в геометрии», в который он гениально уловил в отношении мнимости чисел диалектику
отношения бесконечного к конечному, отношение физического и метафизического
миров. Наш комментарий – в теле фрагмента.
«Обратим внимание, прежде всего, на то обстоятельство, что обрисованная
в «Мнимостях» топологическая модель пространственно-временного многообразия
является, конечно же, незавершенной. Но при всей своей незавершенности она демонстрирует
двойственный характер пространства-времени. «Все пространство, - пишется на стр.51, - мы можем
представить себе двойным, составленным из действительных и из совпадающим с
ними мнимых гауссовых координатных плоскостей, но переход от поверхности действительной
к поверхности мнимой возможен только
через разлом пространства и выворачивание тела через самого себя». Понятие
гауссовой поверхности означает здесь криволинейную поверхность, кривизна
которой отличная, вообще говоря, от нуля. Изогнутая поверхность берется для
того, чтобы сделать абсолютным различие между ее лицевой (действительной) и обратной (мнимой) сторонами, заполненными
соответственно вещественными и мнимыми точками. Ясно, что без нарушения логического
закона тождества нельзя представить себе, чтобы две разные точки –
действительная и мнимая – совпали между собой. Но тогда возникает вопрос: как
же могут совпадать между собой две разные поверхности – та, что составлена из
действительных точек, и та, что составлена из мнимых? Из высказывания, помещенного на стр.33 можно
понять, что между каждыми двумя спаренными точками – действительной и мнимой –
должно быть некоторое расстояние, которое Флоренский отождествил с
дифференциалом Лейбница. Но в то же время он еще не мог оперировать в полной
мере понятием бесконечно малой величины в актуальном смысле, разработанным
несколькими десятилетиями позже в новой
отрасли математики – нестандартном, или не-архимедовом анализе.
Следовательно, при доработке топологической модели требуется
восстановить, по крайней мере, одно недостающее в ней звено. При этом полную
ясность обретает центральная идея всего построения – идея двойственности
пространственно-временного многообразия, утверждающая существование в нем
внутренней стороны, изнанки, наряду с внешними атрибутами – протяженностью и
длительностью.
Для Флоренского математический вывод о существовании «изнанки»
пространства-времени был, однако, не самоцелью, а средством представления в
терминах пространства и времени человеческой мысли, которая со времени Декарта
считалась непротяженной, а потому и внепространственной. На самом деле можно
представить себе и внепротяженную мысль, разлитую в мировом пространстве, если
она обладает свойством мгновенно связывать любые пространственно удаленные
объекты, способные реагировать на её влияние. Поиск ответа на вопрос, какой
должна быть структура пространства и времени, чтобы она согласовывалась со
столь необычными, с точки зрения здравого смысла, явлениями – вот то,
по-видимому, главное, что стимулировало работу над «Мнимостями в геометрии».
Поскольку исследование данной проблемы не ограничивалось геометрическими
построениями, а выверялось, как мы уже сказали, на разных уровнях рассуждений,
нельзя без хотя бы краткого ознакомления с ними оценить масштабы всего замысла».
Итак, у нас есть «идея
двойственности пространственно-временного многообразия, утверждающая
существование в нем внутренней стороны, изнанки, наряду с внешними атрибутами
– протяженностью и длительностью». Во-первых – не «двойственности», которая
есть результат разделения, но
бинарности, как целостности воспринимаемой в виде своих проекций. Во-вторых, существование «изнанки» и «внутренней стороны» предполагает именно существование глубины, пространственности, пространства
большего числа измерений. В-третьих, вход в это пространство осуществляется
через «разлом» и «выворачивание тела через самого себя», т.е. своего рода уже
не раз используемое нами выражение «выворачивание наизнанку».
Далее, для Флоренского вывод о существовании некоей
«изнанки», или как у нас определяется «внутренней глубины», «внутреннего
пространства» был не самоцелью, а «средством представления в терминах
пространства и времени человеческой мысли, которая со времени Декарта считалась
непротяженной, а потому и внепространственной». Кроме этого, данная своего рода
над- или внутрипространственность мышления и мысли влечет за собой то
обстоятельство, что человеческая мысль является живой частицей Пространственной
Мысли.
«2. Логико-арифметический способ выражения связи между двумя видами
реальности
В 1917 г. Флоренский опубликовал книгу «Данные к жизнеописанию
архимандрита Серапиона (Машкина)». Удивительную, полную
непрерывных изысканий жизнь, как видно по данной книге, прожил Серапион Машкин
(1854-1905). Образование начал в частном классическом пансионе, затем прошел
пансион школы Правоведения. Поступление экстерном в Морское училище, окончание
его в звании гардемарина. За 1,5 года дослужился до мичмана. Затем отставка.
Через год – это было в 1877 г. – поступление на естественное отделение
физико-математического факультета Санкт-петербургского университета. Неполный
университетский курс, затем поездка на Афон и проживание там в течение 5 лет. И
сорокалетние поиски решения проблемы,
которая постоянно стояла в центре внимания Серапиона. Это была проблема
обоснования сознания и самосознания человека.
Церковь традиционно утверждала, что в основе человеческого сознания и
самосознания лежит присущий человеку дух, приобщаемый к мировому духу на путях
молитвы и аскезы. Но не каждый был способен проникнуться таким мироощущением. В
науке велись параллельные поиски связи между духом и телом человека в частности
и между внеэмпирической и эмпирической реальностями вообще. Свыше сорока лет
усилий – и Серапион самостоятельно пришел к тому же выводу, к которому в свою
очередь в какой-то мере подвело развитие математики в целом. А именно, что
связь между двумя видами реальности выражается в математических понятиях с
помощью понятия актуальной бесконечности.
Вот как описывает это открытие сам архимандрит Серапион. Раскрыть
сущность сознания и самосознания можно только – к такому выводу он пришел –
исходя из требований самообоснованности и самодоказательности. Но за этими
терминами вовсе не скрывается какая-то тавтология. Самообоснованность
выражается идеей актуально заданного целого, полагание которого требует бесконечного ряда актов отнесения одного к
другому. «Эта Бесконечность, указывал Серапион, - действительно самообосновывается, так как в ней дан бесконечный ряд, она не обрывается
на первом, не выводимом из другого, просто данном, а восходит в бесконечность,
причем этим не отодвигается только решение – первое, чтоб никогда не быть
данным (в этом отодвигании в неопределенность опять нет решения), а напротив,
дается бесконечность как своего рода конечность, или, лучше сказать,
определенность как бесконечная Единица.
После многолетних исканий, комментирует данное открытие Флоренский,
упорным трудом самостоятельной мысли о.Серапион вышел, наконец, хотя и с другой
стороны, к тем же результатам, к которым пришла математика в лице Г.Кантора. То
же можно сказать, судя по данной книге, и о самом Флоренском.
Надо особо сказать и особо признать,
что всякого свободно мыслящего человека от любого иного отличает простая способность
увидеть ИМЕННО – «самообоснованность» бесконечного собой, всей совокупностью
того, что она составляет! Гениально, просто – и потому гениально-просто!
Бесконечное находит своё
основание – «самообоснование» – в самом себе как бесконечной совокупностью
конечного. Формальный ум видит конечную форму и более ничего. Мыслящий разум
видит в конечной форме и всех иных конечных формах – основу бесконечного, как
необходимое основание Единого, Целого – Единицы, которая определяет все свои
бесконечные частности точно так же, как все эти конечные формы-частности
определяют бесконечное, аформальное Единое. Сорок лет понадобилось очень
неглупому и чрезвычайно устремленному человеку, чтобы понять эту простоту
сосуществования и взаимной обусловленности бесконечного и конечного.
Почему же столь важна здесь идея
актуальной бесконечности? Важность её становится очевидной, если хорошенько
присмотреться к такому, с виду простому, объекту математики, как натуральный
ряд чисел 1,2,3,…,n… .
Идея потенциальной осуществимости в нем вполне понятна. Мы можем опираться на
нашу историческую память – память о наших прошлых действиях – чтобы каждый раз,
сделав n-ый шаг, т.е.
дойдя до числа n,
вспомнить о том, что мы неизменно пользовались знаками «+» и «1» в предыдущих
шагах, а потому допустим и следующий шаг в виде (n+1). Идея актуальной бесконечности
превращает потенциально осуществимую последовательность натуральных чисел в
последовательность законченную, данную одновременно всеми своими членами.
Эмпирики, кои в математике представлены когортой интуитивистов и конструктивистов,
утверждают, что идея актуальной бесконечности ведёт к логическому абсурду, так
как нельзя логически непротиворечивым образом представить себе неограниченную
последовательность объектов, имеющую начало, но не имеющую конца, несмотря на
то, что все объекты, начиная с первого, расположены в строго определенном (индуктивном ) порядке. И
они в своём эмпирическом созерцании правы. Но эмпирики не понимают того, что
актуальной бесконечностью перекидывается мост от одного вида реальности к
другому, и потому хотя идея актуальной бесконечности и приводит к ряду
логически противоречий, но последние не являются логическим абсурдом: они
выявляются в математических рассуждениях при самом строгом соблюдении всех
законов элементарной логики и именуются антиномиями. […]
Обратим особое внимание на
то, что ведущим признаком,а и скорее даже неизбежным
следствием формальности мышления является стремление этого мышления
отрицать само наличие существования актуальной бесконечности! Бесконечное актуальное, являющееся сущностью
всякого общего,
отрицается точно так же как отрицается существование, например,
Всеобщего-Бога! Рассудок как здравый
бухгалтер-учетчик рациональных форм просто не в состоянии получить и охватить
бесконечность, ибо бесконечное – бесформенно, лишено какой-либо здравой, т.е.
«рациональной» формы, бесконечное – парадоксально и к тому же всегда приводит с собой «лютого зверя» противоречия которого буквально «как черт
ладана» страшится рассудок!
Можно ещё раз повторить, что для
детей бесконечность воистину непостижима, даже если такое «дитя» уже
облысело на научной ниве, а с группы не по-детски блестящих ученых лысин легко
можно натрясти кучу песка для любой научной песочницы, чем собственно такого
рода ученый люд и занимается.
Теория Кантора, ведущая к формулировке соответствующей антиномии,
сводится к утверждению, что любое произвольное множество нельзя однозначно
отобразить на множество его подмножеств (множество-степень): множество-степень имеет большую мощность, чем
исходное множество. Если взять теперь множество всех множеств, мы придем к противоречию в оценке его мощности. В самом деле, пусть М будет
множеством всех множеств. Его множество-степень U, в соответствии с формулированной выше
теоремой, должно иметь мощность большую чем мощность множества М, что
парадоксально по той причине, что М, по определению, есть множество, содержащее
все множества и потому имеет наибольшую мощность […].
Истина есть соответствие одного другому, но истине положены конечные
пределы, выход за которые превращает её в ложь. Осознание таких пределов –
предпосылка возникновения родового сознания человечества и сознания отдельного
человека. Флоренский о границах истинной мысли пишет следующее: «В
неопределенной возможности, мысли пред-лежащей, - двигаться всячески, в безбрежности моря мысли, в
текучести потока её ею же ставится себе твердые грани, неподвижные межевые
камни, и притом ставятся как нечто клятвенно признанное нерушимым, как ею же
установленное, т.е. символически, посредством некоторого сверх-логического акта, волею сверх-личною,
хотя и проявляющеюся через личность, воздвигнутые в духе конкретные
безусловности: и тогда возникает сознание». Условие его
возникновения – включение – включение мыслительной способности человека во
вселенский
 . […]
. […]
Здесь Флоренский говорит о
самом важном акте, акте возникновения сознания, акте охвата
пред-мыслью пред-сознания самой себя – себя как момента пред-личности, и этот переход через границу, где границей
является становящаяся личность, то
есть сверх-личный, и в силу этого и сверх-логический акт порождает сознание. Сознание – по сути дела это
определенной меры плотности фронт волны чувственного отрывающегося от центра самости, т.е. самоощущаещего «я» и переходящего в
«свободное», но контролируемое центром притяжения существа «орбитальное
движение».
Математика с давних пор занята исследованием метрических и
топологических характеристик пространственно-временного многообразия. Но все
традиционные исследования оставались как-то в стороне от вопроса, поставленного
Флоренским, а именно от вопроса о существовании внутренней стороны, «изнанки»
пространства-времени. Возможно, это обусловлено тем, что допущение о
двойственном характере пространственно-временных отношений неизбежно упирается
в те самые антиномии, для которых не существовало, до работ Н.А.Васильева,
логического оправдания. Теперь страх перед противоречиями-антиномиями
окончательно преодолен. И сама математическая логика становится ориентиром в
поисках необычного, неосязаемого, сверхэмпирического в пространственно-временном
универсуме. Первый шаг на данном пути – открытие фактора поляризации
пространственно-временных отношений на внешние и внутренние. Последний шаг –
завершение построения геометрической модели Флоренского. […]
К.Гёдель заметил, что парадоксы теории множеств представляют собой очень
серьезную проблему, но не столько для математики, сколько для логики и
философии. За этим высказыванием скрывается, похоже, следующее обстоятельство.
Исходным отношением математической теории множеств, как и в логической теории исчисления
классов, служит отношение принадлежности элемента множеству (классу). Но
множества бывают разные. Одно дело – принадлежать натурального числа, допустим,
числа 5, множеству натуральных чисел, другое дело – принадлежность Земли множеству больших планет Солнечной системы. В
первом случае отношение принадлежности оправдывается теоретической
необходимостью, во втором – эмпирической схемой обобщения. Понимание этого
крайне важного обстоятельства и наводит естественным образом на мысль о том,
как разрешить антиномию. […]
Здесь же наша задача состоит в том, чтобы расселовскую конъюнкцию
оппозиции распространить на многомерные предикаты, причем такие предикаты,
которые могли бы быть представлены пространственно-временные отношения. В
практике научного исследования мы привыкли иметь дело с тем типом этих
отношений, в которых не фиксируются какие бы то было конкретные (частные)
атрибуты вещей. Такие отношения задаются сугубо экзистенсиональным способом и
называются внешними. Они
действительно имеют внешний характер в том смысле, что свойства вещей остаются
безразличными к ним и не меняются с их изменениями. Однако попытка свести
всевозможные пространственно-временные отношения к внешним приводит примерно к
такому же парадоксу, как антиномия Рассела. Т.е. наряду с внешними отношениями
выявляются внутренние пространственно-временные отношения так, что оба типа отношений взаимно
исключают и дополняют друг друга. Из противоположного характера внутренних
отношений следует, что свойства и состояния объектов, вступающих в данные
отношения, зависят от самих этих отношений и вне их просто не существуют.[…]
Сколько-нибудь общепринятого взгляда на природу связи между внешними и
внутренними отношениями до сих пор так и не сложилось. Известно, что логически
позитивисты – Б.Рассел, Л.Виттгенштейн и др. – признавали только отношения
внешние. Внутренние же – изгонялись как из логики, так и философии. «Внешние
отношения, - пишет разбирая данный вопрос Б.Дальбом, - использовались Джеймсом
Муром и Расселом в качестве главного оружия против идеализма. Центральное
значение имели, конечно, те отношения, которые соотносят познающего с
познаваемым, перципиента и его ощущения с воспринимаемым объектом и т.п., где
внутренние отношения обеспечивают интимную сторону идеализма, которая была
утрачена, когда уверовали в то, что эти отношения внешние».
Какими бы ухищрениями не
пользовалась формальная логика, но она не может не остаться логикой форм,
логикой внешнего.
На пути к полному выяснению данного вопроса находились исследования
Флоренского. Он определил внутреннее отношение между двумя объектами,
разнесенными в пространстве, как особый путь между ними, по которому расстояние
между тем и другим оказывается равным нулю. Геометрия учит, - указывал он в
одном месте, - что каково бы ни было расстояние между двумя точками в
пространстве по кратчайшему между ними, - кроме того всегда может быть
осуществлен путь, по которому расстояние равно нулю. Линия этого пути есть так
называемая изотропа. Устанавливая сообщение между двумя точками изотропическое,
мы непосредственно соприкасаем друг с другом любые две точки». Геометрия, в которой
исчезает расстояние между двумя пространственно удаленными друг от друга
точками, и создавалась автором путем расширения её точечного многообразия до сочетания
действительных и мнимых точек.[…]»
(Конец
цитируемого фрагмента)
Всеобщая связь всего – связь
через всеобщее, т.е. такая связь, такое отношение, в котором любая точка
непосредственно соотносится с каждой точкой…
Образно и очень точно такую
картину всеобщей связи всего как некоего результата Творения выразил Ауробиндо:
«Что же есть завершение всего? Подобными меду, что может попробовать
себя и разом все свои капли, все капли которого могут попробовать друг друга, а
каждая капля отведать все медовые соты целиком, как саму себя, должны быть в
итоге Бог, душа человеческая и вселенная».
Итак, для того чтобы
напомнить о внутренней логике, на которую мы будем опираться в своих действиях
ещё один важный фрагмент из работы А.Ф.Лосева:
«В
диалектике операции извлечения корня мы увидим, что извлечение корня и
возведение в степень относятся к области алогического становления, в частности
к области органического роста бытия, в отличие от остальных арифметических
действий, которые мыслятся как механические или усложненно-механические.
Возводя в степень, мы заставляем данное число повториться в каждом своем
элементе; а извлекая корень, мы находим в нем то первоначальное основание,
в подлинном смысле «корень», из которого [бытие] появилось путем самоповторения
во всех своих отдельных элементах. Это и есть признак организма — вещественное,
субстанциальное повторение целого в каждой отдельной части и вытекающая отсюда
невозможность существования этих частей в изолированном виде. Что значит в этом смысле извлечь квадратный корень?
Это значит найти такое первоначальное основание отрицательности, откуда она
появляется путем однократного
самоповторения во всех своих основных элементах.
Откуда появляется мыслимость единицы (отстраняющая реальную субстанцию
единицы) и откуда само отрицание, если процесс этого появления есть некое самоповторение? Отрицательная единица есть
чистая мыслимость единицы, отстраняющая, отталкивающая реальную единицу; откуда происходит это отстранение и
отталкивание, и почему оно есть результат некоего самоповторения, и что именно
повторяет тут себя самого в себе же самом?
4. Вот тут-то и рождается категория твердой
очерченности и оконтуренности числа,
той его абсолютной неупругой структурности и образности, перспективности, которая впервые и рождает
самое число. Как возможно отрицание чего-либо? Только путем проведения границ, точно отделяющих его от
всего иного. Мыслить отрицание единицы —
значит мыслить ее границы со всем прочим, что не есть она сама, границы,
отделяющие ее от всего прочего. Значит, корень отрицания единицы есть корень, из которого вырастают границы единицы,
отделяющие ее от всего прочего. А квадратный корень из отрицательной единицы
есть корень, из которого вырастают
границы единицы, если их повторить на всем их протяжении. От чего отталкивается мысленная единица, когда
она функционирует как отрицательная? Она отталкивается от <...> субстанции единицы, но это может значить только то, что реальная субстанция единицы имеет
твердые контуры, от которых и происходит отталкивание. Раз ставится вопрос об отталкивании, то тем самым
предполагается, что есть нечто твердое,
от чего и происходит отталкивание. Следовательно, реальная субстанция мыслится
здесь как твердая, т. е. имеющая
определенную негибкую форму. Надо, чтобы эта форма была; и надо, чтобы от этой
формы мы отошли и созерцали ее издали, чтобы вообще могло
состояться суждение о границах и, значит, об отрицании. Когда проведены
границы, то, как это ни [не]обходимо для четкого созерцания предмета, границы, сами по себе
взятые, тем самым еще не фиксируются
специально. Ограниченность имманентно сопровождает всякую мыслимость, но чтобы созерцать специально ограниченность,
границы, надо выйти за пределы этих границ или, точнее, надо просто различать
уже не просто всю вещь от инобытия, но только одну ее границу от инобытия, а
это значит — еще раз повторить эту границу в ней же самой, т. е. изменить эти
границы, сохраняя не форму, но какую-нибудь (пусть хотя бы
бесконечно-малую—этого вполне достаточно) величину. Это и значит извлечь квадратный корень из отрицательной единицы. Таким
образом,
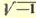 есть не что иное, как полагание твердо
очерченной границы, или перспективно сформулированного образа, для отвлеченно взятой единицы, осуществление
и утверждение оконтуренности единицы.
есть не что иное, как полагание твердо
очерченной границы, или перспективно сформулированного образа, для отвлеченно взятой единицы, осуществление
и утверждение оконтуренности единицы.
5. Тут еще не вскрыты все стороны мнимой величины, но покамест указана
только одна существенная сторона. Однако тут вскрыто все, что содержится в
конструкции
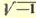 .
Как скоро увидим, другие методы представления мнимой величины дадут и другие
стороны в диалектике самой категории мнимого. Прежде чем перейти к этому,
повторим еще раз в строго последовательной форме диалектику
.
Как скоро увидим, другие методы представления мнимой величины дадут и другие
стороны в диалектике самой категории мнимого. Прежде чем перейти к этому,
повторим еще раз в строго последовательной форме диалектику
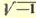 .
.
а) Единица есть утверждение, субстанция, и отвлеченная, абсолютная единица есть
утверждение и субстанция в мысли, в
идее, идеальное утверждение. Положительная единица есть новое утверждение, т. е. утверждение утверждения, реальное утверждение
идеального утверждения. Отрицательная же единица есть новый переход в сферу идеи и смысла, но переход не
с целью забвения реальности (тогда это была бы абсолютная единица), но с целью
активного ее отрицания. «Минус единица» есть мысленная, идеальная единица, отталкивающая реальную единицу. Другими
словами, (—1) есть оформление единицы, взятое в активном отстранении реальности
единицы. Такое оформление реального, которое отстраняет саму реальность, есть чистая форма <...>, его
смысловой образ.
b) Извлечение
корня из какого-нибудь числа есть операция, отражающая то первоначальное ядро числа, откуда появилось само число через свое
алогическое становление путем реального
самоповторения и самоотражения себя
самого в себе же самом, т. е. это есть арифметическое выражение живого роста
организма. Извлечение квадратного корня
из числа есть операция выявления его
указанного ядра, когда оно дорастает до данного числа путем однократного самоповторения (самоотражения).
с)
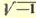 следовательно, есть выявление такого первоначального ядра и основания смысловой
образности числа, когда оно дорастает до этой образности путем однократного
самоповторения (самоотражения, самоотличения).
следовательно, есть выявление такого первоначального ядра и основания смысловой
образности числа, когда оно дорастает до этой образности путем однократного
самоповторения (самоотражения, самоотличения).
d) [1.] Это
первоначальное ядро и основание числа должно поэтому претерпеть самоповторение,
т. е. прежде всего самоотличение, но не то первоначальное самоотличение, без которого это ядро вообще
не могло бы существовать «...> правилам диалектики), но то самоотличение, которое отличает от инобытия,
не есть принцип, а уже утвержденный принцип, т.е. отличает реальность с
определенными границами, самоотличение, которое отличает от инобытия самые границы числа; это самоповторение есть
результат квадратности извлекаемого здесь корня. 2. Это основное ядро, или
основание, числа должно здесь мыслиться как нечто твердое и абсолютно негибкое, ибо оно выдерживает на себе
отталкивание, приносимое смысловой образностью (в случае отрицания), т. е.,
другими словами, искомое ядро, или основание смысловой образности, числа должно быть твердой, абсолютно твердой оконтуренностью числа, и только тогда эта
последняя и может обусловить собою, путем самопротивопоставления,
конкретно-смысловую образность числа.
3. Наконец, поскольку это самопротивопоставление и самоотрицание
мыслится, по условию, органически, как живой рост организма, оно должно
пониматься так, чтобы указанное ядро, т.
е. первоначальная, абсолютно-твердая оконтуренность, органически дорастало до конкретной образности числа, чтобы оно
было живым скелетом живого числового
тела. Это значит, что в той деформации,
которую претерпевает [числовой] контур, целиком присутствует самый контур, т. е. то целое, бывшее вначале, остается целым и для того нового, что из него
получилось путем деформации.
е) Сводя все вышеуказанное к одной максимально сжатой формуле, можно
сказать так. Все, что мыслится, и,
следовательно, также число, чтобы мыслиться, должно иметь свои границы, но это
еще не значит, что тут фиксируются самые границы. Чтобы фиксировать самые
границы, необходимо уже их отличать как таковые от всякого инобытия. Но это
значит, что тут фиксируются не границы, но границы границ, т. е. форма границ,
образ ограниченности. Мнимая величина и [есть] форма и вид, образ ограничения
числа, форма формы числа, число как смысловая перспектива».
Итак,
«Все, что мыслится, и, следовательно, также число, чтобы
мыслиться, должно иметь свои границы, но это еще не значит, что тут фиксируются
самые границы. Чтобы фиксировать самые границы, необходимо уже их отличать как таковые от всякого инобытия. Но это
значит, что тут фиксируются не границы,
но границы границ, т. е. форма границ, образ
ограниченности. Мнимая величина и [есть] форма и вид, образ ограничения
числа, форма формы числа, число как смысловая перспектива».
Вспомним:
«Кратко говоря и формульно выражаясь, числовая форма «5»
есть не только «5», но нечто иное, формально неотличимое от «5», а если
выразиться точно: «5» + нечто.
Что же это «нечто» собой представляет?
Очевидно, что в числовом смысле это может быть лишь числовой разностью: «5–5=0»…
Но «0» в выражении количественного отношения двух величин также есть
лишь формальная фиксация формального результата предельного перехода некоторого значения, предел которого и равен
«0».
Предел чего равен «0»?
А) Предел бесконечно малой (т.е.
стремящегося к нулю действительного числа);
Б) Предел комплексного числа,
мнимая компонента которого стремится к нулю.
В) Предел комплексного числа,
действительная и мнимая компоненты которого стремится к нулю».
А (Абсолютное Число) тождественно равно Себе:
А = А…
Но абсолютная
тождественность внутри себя самой должна выявлять различие с Собой:
«А» – «А» = «0»…,
где «–» рефлексивная операция различения-отождествления, в отношении
чистой количественности имеющая смысл «числовой количественной разности»
Но «0», являясь формой как
результатом, т.е. формой как проекцией,
имеет и содержание – причину результата, включающую в себя и проецируемое, и пространство проекции, и производящего проецирование: «0ί»,
«a + bί»…
Понятно и очевидно, что Форма
Абсолютного, пребывая в Своём Пространстве, являет собой абсолютность всех форм,
проекции которых тождественно равны друг
другу и соответственно тождественно равны трансформальному «0» как
трансформе всех трансформ.
Таким образом, в
недвижимость абсолютной тождественности, в её абсолютные глубины силой самой идеи тождественности входит движение отождествления, которое в свою
очередь включает в себя все моменты движения самоотличия себя от себя, а всё в
целом составляет движение рефлексии
тождества. Кроме этого, необходимое качество бесконечности такой рефлексии и потому её необходимой замкнутости на себя,
что является проявлением качества единственной формы движения Абсолютного – вращения, позволяет тождественность и
самотождественность Абсолютного представить как процесс бесконечное отождествление Относительного Абсолютного в Себе Самом.
На Высших ступенях бесконечной лестницы такого движения, уходящей в Абсолютные
Небеса, это движение проявляется как Движение Космического Разума. Какова же в
такой картине роль и значение разума человеческого?
Человек образно выражаясь, лишь в лучшем случае одной ногой стоит
на первой ступени этой лестницы, ведь абсолютное большинство «стоит», т.е. опирается на эту низшую ступень руками.
Если учесть, что двигаться
на четвереньках по такой лестнице
невозможно… то, можно догадаться о неизбежной судьбе такого человечьего «стояния
в разуме».
Итак, нет ничего удивительного в том, что хорошо всем
известная формальная структура
комплексного числа является универсальной структурой формы всей
противоположной Абсолютному А-числу А-мнимой иерархии математических числовых форм.
Глубокое кватерниональное заблуждение Гамильтона, повлекшее тяжелые, длительные но,
по сути, неизбежные формальные блуждания всей современной физики и математики,
черпает свою силу в невинном формализме математического софизма, когда сугубо
формальная форма т.н. действительного числа, являющегося в действительности α-мнимой формой абсолютного числа, принимается
за необходимое, то есть трансформальное, истинное основание:
«Кватернионы
можно определить как формальную сумму
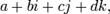 где
где
 —
вещественные числа, а
—
вещественные числа, а
 — мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов —
— мнимые единицы со следующим свойством: i2 = j2 = k2 = ijk = − 1. Таким образом, таблица умножения базисных кватернионов —
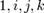 —
выглядит так:
—
выглядит так:
например,
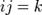 ,
a
,
a
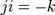 .»
.»
Итак, у нас есть комплексное
число с = a + bi, где «а» т.н. действительная, а «b» -
т.н. мнимая часть комплексного числа,
ί – т.н. «мнимая единица».
Очевидно, что если b → 0, то с → a.
Ключевой во
всей истории возвращения математики в истинное числовое пространство является очевидность того, что действительное число, является частным
случаем или проекцией комплексного
числа, и так же, как формальное
проецирование превращает комплексную числовую форму в действительную,
операция противоположная формальному проецированию – восстановление
числового первообраза по имеющейся проекции – превращает действительное число в комплексное.
Итак, числовым первообразом
(формой формы) т.н. действительного числа является комплексное число. Таков исходный пункт нашего строительства числового
поля (пространства).
Логика построения числового комплексного пространства
предельно проста. Действительные составляющие самого комплексного числа: с = a + bi, имеют
соответствующую комплексную структуру, которая в свою очередь также имея в
наличии действительные числа-компоненты, может быть представлена в комплексной
форме и т.д.
Такова логика восстановления
по отпечатку-форме – первообразной формы (формы проецируемой формы) результат проецирования которой породил данный
отпечаток-форму.
Такова и логика построения числовых
пространств высшего ранга, в которых когда-то чисто количественные,
наипростейшие значения становятся очень
сложными символами-значениями, которые человеческое сознание интерпретирует в виде потоков переживаний, чувств и наконец того, что принято называть мыслями, а особые формы таких потоков
мыслей являют собой спекулятивные понятия – истину
абсолютности, к которой человеческое сознание уже может прикоснуться.
Но рассмотренное представление самоопределения
полей чисел и интерпретация действительных чисел как α-комплексных, а
комплексных как β-комплексных была бы неполной, если бы не было показано как на основе изложенной трансформальной
теории чисел могут стать решаемы фундаментальные задачи, стоящие перед
наукой.
Покажем это на примере исследований В.И.Елисеева, прежде
всего его монографии «Введение в методы теории функций пространственного
комплексного переменного».
Порядок рассмотрения будет следующим – фрагменты книги
и цитаты из неё будут перемежаться с необходимыми комментариями. При этом мы совершенно не будем рассматривать многочисленные приложения развертываемой В.И.Елисеевым теории, которую он называет «теорией
пространственного комплексного переменного», безусловно заслуживающих отдельного и внимательного изучения.
«Теория функций комплексного переменного ТФКП дошла до наших дней почти
в том виде, в котором оставил нам ее создатель великий французский математик
Огюстен Коши (1789-1857 гг.).
Связность функций на комплексной плоскости наиболее адекватно отражает
ту связность, которая существует в реальных физических процессах. Методы ТФКП
применяются во всех областях математического естествознания, начиная от
макромира и кончая микромиром. Алгебра комплексных чисел отвечает классическим
операциям над действительными числами. Поле комплексных чисел получено из поля
действительных чисел присоединением лишь одного корня квадратного уравнения, не
имеющего решения на действительной оси. С точки зрения современной абстрактной
алгебры поле комплексных чисел алгебраически замкнуто, то есть, рассматривая
корни многочленов, нельзя получить новых чисел.
Связность пространства, адекватно отражающего связность реального мира,
требует создания аппарата комплексной пространственной алгебры с законами
действительных и комплексных чисел. Эта связность определит в пространстве те
геодезические линии, движение по которым является одним из математических
условий, лежащих в основе теории гравитации.
Теорема Фробениуса отрицает возможность расширения поля комплексных
чисел с коммутативным законом умножения элементов, то есть умножением,
результат которого не зависит от перестановки сомножителей.
До настоящего времени считается невозможным обобщение числа в
пространство. Совсем недавно математик Л. С. Понтрягин писал, “что никаких
других логических возможностей для построения приемлемых в математике величин,
аналогичных действительным и комплексным числам, кроме действительных и
комплексных, не существует».
Исследователи за 140 лет после О.
Коши не справились с основной проблемой математики – расширения поля чисел в N-мерное
пространство с соблюдением законов алгебры действительных и комплексных чисел.
Попытка расширить поле комплексных чисел натолкнулась на появление новых
чисел- объектов, свойство которых до настоящего времени не поддавались
исследованию. Эти объекты получили название делителей нуля. Произведение двух
чисел равно нулю, если одно из них равно нулю, а второе не равно нулю. Это
тривиальный результат. Появились новые числа не равные нулю, дающие в
произведении нуль. Исключить появление этих чисел возможно путем отказа от
коммутативности умножения. В результате появились алгебры со скалярным,
векторным, спинорным и тензорным умножением и т. д. Все это тупиковые варианты
как показывает жизнь, которые постепенно обречены на вымирание».
Теорема Фробениуса описывает «все конечномерные
ассоциативные действительные алгебры без делителей нуля», доказана Г.
Фробениусом. Теорема утверждает, что:
1) Поле действительных чисел и поле комплексных чисел
являются единственными конечномерными действительными ассоциативно-коммутативными
алгебрами без делителей нуля.
2) Тело кватернионов является единственной
конечномерной действительной ассоциативной, но не коммутативной алгеброй без
делителей нуля».
Доказано, что «размерность любой конечномерной
действительной алгебры без делителей нуля может принимать
лишь значения, равные 1, 2, 4 или 8».
Теорема действительно права,
т.е. истинна в том, в чём она, безусловно,
права.
Иными словами, ситуация
довольно забавная – невозможность существования расширения поля комплексных
чисел, фактически доказывается исключением условия, которое и является условием такого расширения!
Это условие – отсутствие
т.н. делителей нуля.
В чём суть проблемы?
Вновь обратимся к источнику:
«Появление делителей нуля при росте размерности пространства
закономерный результат, который следовал из теории функций О. Коши. Эти объекты
связаны с пониманием структуры плоскости, задаваемой алгеброй комплексного
числа. О. Коши показал, что на плоскости необходимо рассматривать точку с ее
 -окрестностью.
Этот результат и должен был быть использован при построении и переходе в
трехмерное пространство, когда к комплексной плоскости необходимо восстановить
также комплексную плоскость, свернутую в
-окрестностью.
Этот результат и должен был быть использован при построении и переходе в
трехмерное пространство, когда к комплексной плоскости необходимо восстановить
также комплексную плоскость, свернутую в
 -цилиндр.
Тогда новые объекты – делители нуля, которые подчиняются законам классической
алгебры, получают свое истолкование как числа
с модулем равным корню из нуля и изолированным бесконечным аргументом. Именно, вследствие наличия
изолированного направления, заключенного в третьем
-цилиндр.
Тогда новые объекты – делители нуля, которые подчиняются законам классической
алгебры, получают свое истолкование как числа
с модулем равным корню из нуля и изолированным бесконечным аргументом. Именно, вследствие наличия
изолированного направления, заключенного в третьем
 -цилиндре
корень из нуля в пространстве для этих чисел не равен тождественно нулю.
-цилиндре
корень из нуля в пространстве для этих чисел не равен тождественно нулю.
На действительной оси и в
комплексной плоскости корень из нуля равен нулю. В трехмерном пространстве
положение меняется. Срабатывает
 -окрестность
начала координат. Доказательство
основной теоремы алгебры не отрицает появление новых объектов, так как оно
проведено без учета их свойств».
-окрестность
начала координат. Доказательство
основной теоремы алгебры не отрицает появление новых объектов, так как оно
проведено без учета их свойств».
Исключение делителей нуля из рассмотрения привело к ограничению в
расширении поля комплексных чисел и фактически исключило из рассмотрения
математического естествознания изучение структуры пространства. Изучение
структуры пространства пошло по тупиковым вариантам алгебр с законами операций,
не соответствующих классическим законам чисел».
Несколько слов относительно
терминологии, используемой В.И.Елисеевым.
«
 -окрестность» некоторой точки
или «комплексная плоскость, свернутая в
-окрестность» некоторой точки
или «комплексная плоскость, свернутая в
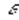 -цилиндр»
есть, конечно, ничто иное как внутреннее
пространство некоторой точки или прямой, проекции которых на действительную
ось представляются формальному уму в виде обычной «точки» (объекта не имеющего
каких-либо реальных размеров) или прямой» (как эвклидовской «длины без ширины»):
-цилиндр»
есть, конечно, ничто иное как внутреннее
пространство некоторой точки или прямой, проекции которых на действительную
ось представляются формальному уму в виде обычной «точки» (объекта не имеющего
каких-либо реальных размеров) или прямой» (как эвклидовской «длины без ширины»):
«Вершиной классической математики и математического анализа является
теория функций комплексного переменного (ТФКП), основателем которой является французский
математик О. Коши. Теория дошла до нашего времени почти в том виде, в котором
она была создана.
Значительно усилив мощь математического аппарата в инженерных расчетах,
теория Коши оставила инженерный аппарат плоским расчетным. Для перехода к
описанию пространственных физических процессов и явлений требуется введение в
аппарат дополнительных координат, которые не соответствуют определению пространственной точки и окрестности ее, которая заложена в теории Коши. В теоретической физике например, вводят матрицы, которые ближе к программному обеспечению чем
к математическому аппарату.
Для описания пространственных явлений и процессов исследователи строят свои конкретные физико-математические модели. Инженерный расчет достигает успеха лишь в том случае,
когда он проводится с соблюдением законов алгебры обычных чисел.
Сложность физических процессов, например, на уровне атомного ядра и
электронных оболочек требует
создание эффективной пространственной
модели.
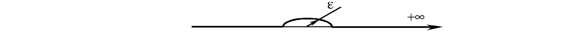
Рис. 1. Ось в комплексном пространстве
Теория Коши в этом плане дает предпосылки для построения такой
пространственной модели и она используется в теоретической физике. Теоремы Коши об изолированных точках и
вычетах, а также взаимосвязь точек на плоскости комплексных координат дают основание на пересмотр абстрактного понятия точки. Рассмотрим последовательно: линию, плоскость, пространство, опираясь на принятые понятия, но делая свои выводы.
Линия рассматривается как одномерное пространство, как и делают современные исследователи. Однако как только на линии ставится точка
ноль, как начало координат, что означает на инженерном языке привязку этой линии к реальному пространству, назвать линию одномерным пространством означает
допустить грубейшую ошибку. Переход по линии из −∞ через точку 0 к ∞ + нельзя не
обогнув 0 по дужке и совершив оборот на угол ϕ =± π.
Можно игнорировать этот факт,
называя линию одномерным пространством, но можно утверждать, что линия терпит разрыв в точке начале координат, какой
бы минимальный радиус
Дужке 0 → ε не был, либо это уже не одномерное
пространство.
Далее рассматриваем установившееся понятие двумерного (плоского) пространства. Если плоскость рисуется без начала
координат, то это понятие не несет физического смысла. Если плоскость привязана
к реальному пространству, то в ней фиксируется начало координат. В этом случае
логика предыдущих рассуждений вступает в силу. Окрестность нуля не принадлежит
этому двумерному миру. Окрестность нуля выколотое двумерное пространство. Определение, ноль имеет неопределенный аргумент 0 = 0eiϕ, физически означает, что плоскость проколота
лучом, исходящим из другого измерения. Последнее и утверждает, что плоскость
несет в себе элемент пространства.
Рис. 2. Комплексная плоскость
Нельзя пройти точку ноль по прямой, не обогнув ее по дужке в его
окрестности. Можно радиус дужки устремить к нулю, однако физическая сторона и в
этом случае не меняется. Определение нуля как 0 = 0eiϕ в физических расчетах
дает возможность игнорировать аргумент в точке ноль, до тех пор как ноль не
становится критической точкой. Простейшую кривую на плоскости окружность нельзя
стянуть в точку около критической точки.
Продолжая эту логическую цепочку, восстановим к плоскости не линию,
как это делает классическая математика, а цилиндрическую трубочку радиуса окрестности нуля. Сфера в таком пространстве является сферой с
проколотыми вершинами. Пространство внутри сферы между ее внутренней поверхность и наружной поверхностью цилиндрической
оси есть пространство другого измерения,
чем пространство вне сферы и внутри изолированной оси».
Подобно тому, как
неограниченный рост количественности (абстрактного количественного значения
параметра) так или иначе, приводит к тому, что абсолютная количественность бесконечного становится качеством, т.е. невозможностью дальнейшего роста
количественности, так и бесконечное уменьшение ведёт к тому же. Образно-формальная картина реализации подобного –
достижение кольцеобразной структуры числа и «проникновение» вовнутрь её, в
первом случае – при бесконечном возрастании числа – так сказать «внешней», во
втором – при бесконечном уменьшении и стремлении к нулю – «внутренней».
Так вхождение в новое
числовое качество оказывается действительным вхождением в новое измерение. Границей такого измерения с формально-умозрительной
стороны является такая окрестность точки, в которой количественное неотличимо от качественного и стало им, его форма собственно и есть
кольцо.
Фактически же границей
является само число «0», которое одновременно и принадлежит и не принадлежит
пространству действительной оси чисел, то есть является входом в комплексное пространство.
В.И.Елисеев, если и
несколько формально путается с противоречивыми понятиями, представляя
рассматриваемое нами «кольцо» как «
 -окрестность», но очевидно и фактически,
предмет рассмотрения один и тот же – «движение внутрь точки» в направлении
нового измерения, проекция которого и является «формальной точкой». Кроме того,
все рассматриваемые построения и все числовые пространства находятся именно как
бы внутри точки, то есть ноль является входом в новое измерение, само
осуществление вхождения в новое измерение, например, комплексное пространство, является
как бы «уходом» из измерения, на которое
проецируется внутреннее измерение.
-окрестность», но очевидно и фактически,
предмет рассмотрения один и тот же – «движение внутрь точки» в направлении
нового измерения, проекция которого и является «формальной точкой». Кроме того,
все рассматриваемые построения и все числовые пространства находятся именно как
бы внутри точки, то есть ноль является входом в новое измерение, само
осуществление вхождения в новое измерение, например, комплексное пространство, является
как бы «уходом» из измерения, на которое
проецируется внутреннее измерение.
Теперь относительно так
называемых «делителей нуля».
«Рассмотрим классический ход решения квадратного уравнения
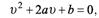
где коэффициенты a, b действительные или комплексные. Произведем последовательно операции»
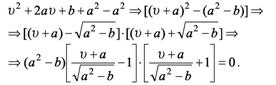
Считаем
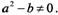 Произведение двух сомножителей XY равно нулю в
трех случаях:
Произведение двух сомножителей XY равно нулю в
трех случаях:
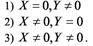
Третий случай определяет произведение делителей нуля. Первые два
варианта дают классический случай решения и два корня квадратного уравнения в
действительной и комплексной областях
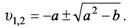
Это тривиальное решение. Исключить из рассмотрения третий случай не
оправдано с логической точки зрения. Два сомножителя не равные нулю, в
произведении дающих ноль, существуют в пространстве комплексных чисел.
Обозначим
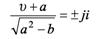
где было введено:
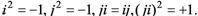
Подставляя выражение в квадратное уравнение, получим произведение
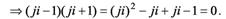
Откуда следует, что квадратное уравнение имеет еще два корня
в пространственном поле чисел
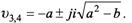
Ввиду того, что (ji)2 =1 отыскание
корней не представляет трудностей.
Появление коэффициента ji перед дискриминантом в решении квадратного уравнения определяет разветвление в решении в силу изменения размерности
пространства. Квадратный корень имеет разветвление на отрицательное и положительное значение в любой
размерности пространства и поэтому корни являются сопряженными. Поэтому
квадратное уравнение имеет по меньшей мере четыре корня».
Идея расширения поля
комплексных чисел, которую как проблему формулирует В.И.Елисеев и решает её, вообще говоря, находится на поверхности.
Она в логике отношения математической
формы (форм) фиксируемых уравнением –
приравниванием-отождествлением данной формы (форм) с необходимым основанием
этих форм.
F(x)=0;
Если «0» является чем-то
сугубо формальным, т.е. просто арифметическим
нулём и математическая форма – лишь некая абстракция, причём, например,
совершенно оторванная и независимая от иных
форм математической формы, то и результаты решения математического уравнения тривиальны и
в них нет, да и не может быть ничего необычного.
ab = 0;
Тождественность одной из переменных (a или b) нулю, и по
этой причине тождество произведения двух переменных нулю не может вызвать удивления даже у школьника, но если тождество произведения двух переменных равно нулю, но
каждая из них нулю не равна, эта ситуация очень необычна, хотя сам термин встречается
в теории колец.
Связь одной переменной с другой, выражаемая
через их обычное действительное произведение – это связь действительных линейных числовых форм в их моменте тождества с «0»
есть формальная, внешняя связь, связь числовых форм.
Частный случай внутреннего отношения, внутренней связи двух числовых форм – тождество двух форм друг другу
не через формальное, а уже трансформальное основание, приводит к обычному
квадратному уравнению вида - a2 = 0; решение которого, стоить вспомнить
символическое и логическое значение квадратного корня, прямо показывает, наряду с
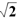 и
и
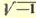 , общий путь расширения-превращения
низшей (формальной) числовой формы в высшую: a=
, общий путь расширения-превращения
низшей (формальной) числовой формы в высшую: a=
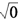 .
.
Таково начало бесконечного
движения к Центру Математического Абсолютного, Центру с формальной точки зрения
находящегося в бесконечности мнимой глубины Его Периферии.
Итак,
«Появление
делителей нуля при росте размерности пространства закономерный результат, который следовал из
теории функций О. Коши. Эти объекты связаны с пониманием структуры плоскости,
задаваемой алгеброй комплексного числа. О. Коши показал, что на плоскости
необходимо рассматривать точку с ее ε - окрестностью. Этот результат и должен был быть использован при построении и переходе в трехмерное пространство, когда к комплексной
плоскости необходимо восстановить также
комплексную плоскость, свернутую в ε - цилиндр. Тогда новые
объекты – делители нуля, которые подчиняются законам классической алгебры, получают свое истолкование как числа с модулем равным корню из нуля и изолированным
бесконечным аргументом. Именно, вследствие наличия изолированного направления, заключенного в третьем ε - цилиндре корень из нуля в пространстве для этих чисел не равен
тождественно нулю. На действительной оси и в комплексной плоскости корень из
нуля равен нулю. В трехмерном пространстве положение меняется. Срабатывает ε -
окрестность начала координат. Доказательство основной теоремы алгебры не отрицает появление новых объектов, так как оно проведено без учета их свойств.
Исключение
делителей нуля из рассмотрения привело к ограничению в расширении поля комплексных чисел и
фактически исключило из рассмотрения математического естествознания изучение структуры пространства. Изучение структуры пространства пошло по тупиковым вариантам алгебр с законами операций, не соответствующих классическим законам чисел».
Таким образом, с теорией
комплексных чисел и комплексных числовых форм, являющихся развитием действительных
чисел мы прощаемся, и переходим к тем математическим формам, которые дали
наименование данной Главе и становление которых происходит исторически строго
параллельно развитию гегелевской философской теории.
Речь идёт о неевклидовой и в общем случае проективной геометрии.
«И вот я хочу рассказать историю о человеческой тупости и о гении… Дело
идет об одном из величайших завоеваний человеческого духа, в котором
участвовали первоклассные таланты и подлинные гении, без преувеличений.
Речь - о неевклидовой геометрии, о ее более чем 2000-летней истории.
История эта очень интересна и поучительна. С ней связано много такого,
что касается не математики самой по себе, а свойств, путей и страстей
человеческих. Но прежде чем говорить об истории, надо бы объяснить
Что такое геометрия Лобачевского…»
Итак, сейчас видимо очень трудно найти такого
человека, который хотя бы что-нибудь не смог
сказать о геометрии Лобачевского, но воистину мало кто точно
знает, что в действительности такое
«геометрия Лобачевского», включая даже тех, кто полагает, что абсолютно точно это знает и потому может
рассказывать о неевклидовой геометрии иным.
Геометрия Лобачевского – одна из особенных форм аформального мышления, то есть
мышления как такового, наряду с иными
формами и той, которая известная как
гегелевская философия абсолютного
идеализма.
Именно в этом в частности и заключается отгадка
загадки тщетности двадцативековых попыток формально вывести т.н. «пятый
постулат» Евклида, так и глубоко, абсолютно обоснованное видение неэвклидовой геометрии как явления
исключительного и революционного.
Диалектика философии Ф.Гегеля и неэвклидова геометрия
явления однопорядковые по значимости по той простой причине, что это
одно и то же явление в двух своих формах.
Далее представлены два весьма интересных для нас письменных
отрывка.
В них, в глубинной логике их единства-противостояния
друг другу, несхожести и кажущегося абсолютного
отсутствия связи друг с другом в действительности скрыты многие тайны, разгадка
которых очень много дала бы человечеству.
Итак, читаем, думаем:
Отрывок первый:
«… Смотри. Здание, громадное,
громадное здание, каких теперь лишь по нескольку в самых больших
столицах, - или нет, теперь ни одного такого! Оно стоит среди нив и лугов, садов и рощ. Нивы - это
наши хлеба, только не такие, как у нас, а густые, густые, изобильные,
изобильные. Неужели это пшеница? Кто ж видел такие колосья? Кто ж
видел такие зерна? Только в оранжерее можно бы теперь вырастить такие колосья
с такими зернами. Поля, это наши поля; но такие цветы теперь только в цветниках у нас.
Сады, лимонные и апельсинные деревья, персики и абрикосы, - как же они
растут на открытом воздухе? О, да это
колонны вокруг них, это они открыты на лето; да, это оранжереи, раскрывающиеся на
лето. Рощи - это наши рощи: дуб и липа, клен и вяз, - да, рощи те же, как теперь; за ними очень
заботливый уход, нет в них ни одного больного дерева, но рощи те же, -
только они и остались те же, как теперь. […] Какая легкая архитектура этого
внутреннего дома, какие маленькие простенки между окнами,- а окна огромные, широкие, во всю
вышину этажей! Его каменные стены – будто ряд пилястров, составляющих раму для
окон, которые выходят на галерею. Но какие это полы и потолки? Из чего эти
двери и рамы окон? Что это такое? серебро? платина? Да и мебель почти
вся такая же, - мебель из дерева тут лишь каприз, она
только для разнообразия, но из чего ж вся остальная мебель, потолки и полы?
"Попробуй подвинуть это кресло", - говорит старшая царица. Эта металлическая мебель легче нашей ореховой. Но что ж это
за металл? Ах, знаю теперь, Саша показывал мне такую
дощечку, она была легка, как стекло, и теперь уж есть такие серьги, брошки, да,
Саша говорил, что, рано или поздно, алюминий {147} заменит собою дерево, может
быть, и камень. Но как же все это богато! Везде алюминий и алюминий, и все промежутки окон одеты огромными зеркалами. И какие ковры на полу!
Вот в этом зале половина пола открыта, тут и видно, что он из алюминия.
"Ты видишь, тут он матовый, чтобы не был слишком скользок, - тут
играют дети, а вместе с ними и большие; вот и в этом зале пол тоже без ковров,
- для танцев". И повсюду южные деревья и цветы; весь дом - громадный зимний сад.
Но кто же живет в этом доме,
который великолепнее дворцов? "Здесь живет много, очень много; иди, мы
увидим их". Они идут на балкон, выступающий из верхнего этажа
галлереи. Как же Вера Павловна не заметила прежде? "По этим нивам рассеяны группы людей; везде мужчины и женщины, старики, молодые и дети вместе. Но больше молодых;
стариков мало, старух еще меньше, детей больше, чем стариков, но все-таки
не очень много. Больше половицы детей осталось дома заниматься хозяйством: они делают почти все по
хозяйству, они очень любят это; с ними
несколько старух. А стариков и старух очень мало потому, что здесь
очень поздно становятся ими, здесь здоровая и спокойная жизнь; она сохраняет
свежесть". Группы, работающие на нивах, почти все поют; но какой работою
они заняты? Ах, это они убирают хлеб. Как быстро идет у них работа! Но еще бы
не идти ей быстро, и еще бы не петь им! Почти все делают за них машины, - и
жнут, и вяжут снопы, и отвозят их, - люди почти только ходят, ездят, управляют машинами.
И как они удобно устроили себе; день зноен, но им, конечно,
ничего: над тою частью нивы, где они работают, раскинут огромный
полог… […]
Но вот работа кончена, все идут к зданию. "Войдем опять в зал, посмотрим, как они будут
обедать", - говорит старшая сестра. Они входят в самый большой из огромных зал.
Половина его занята столами, - столы уж накрыты, - сколько их! Сколько же тут будет обедающих? Да человек
тысяча или больше: "здесь не все; кому угодно, обедают особо, у себя"; те старухи, старики, дети, которые не выходили в поле, приготовили все это: "готовить кушанье,
заниматься хозяйством, прибирать в комнатах, - это слишком легкая работа для других рук, - говорит старшая сестра, - ею следует заниматься тем, кто еще не может или уже не
может делать ничего другого". Великолепная сервировка. Все алюминий и хрусталь; по средней полосе широких столов расставлены вазы с цветами, блюда уж на столе, вошли работающие,
все садятся за обед, и они, и готовившие обед. "А кто ж будет
прислуживать?" - "Когда? во время стола? зачем? Ведь
всего пять шесть блюд: те, которые должны быть горячие, поставлены
на таких местах, что не остынут; видишь, в углублениях,- это ящики с кипятком, - говорит старшая сестра. -
"Ты хорошо живешь, ты любишь хороший стол, часто у тебя бывает такой обед?" - "Несколько раз в год". У них это обыкновенный: кому
угодно, тот имеет лучше, какой угодно, но тогда особый расчет; а кто не требует себе особенного против того, что делается для всех, с
тем нет никакого расчета. И все так: то, что могут посредствам своей компании все, за то нет
расчетов; за каждую особую вещь или прихоть
- расчет".
- Неужели ж это мы? неужели это
наша земля? Я слышала нашу песню, они говорят по-русски. - "Да, ты видишь
невдалеке реку, - это Ока; эти люди мы, ведь
с тобою я, русская!" - "И ты все это сделала?" - "Это
все сделано для меня, и я одушевляла делать это, я
одушевляю совершенствовать это, но делает это вот она, моя старшая сестра, она
работница, а я только наслаждаюсь". -"И все
так будут жить?" - "Все, - говорит старшая сестра, - для всех вечная весна и лето, вечная радость. Но мы
показали тебе только конец моей половины дня, работы, и начало ее половины; -
мы еще посмотрим на них вечером, через два
месяца".»
Отрывок второй:
«Милые дети мои, вашему отцу
тяжело и больно говорить о большинстве натуралистов и в данном деле по
преимуществу о большинстве математиков так, как говорит он. Но как быть! - Эти
господа вынуждают его к тому. Всему должна быть граница. Должна она быть и
невежеству специалистов. И у всякого рассудительного человека есть граница
уступчивости и снисходительности. И наперекор желанию вашего отца он принужден
поставить вопрос: до какой степени понятны большинству господ великих
математиков нашего времени простейшие, фундаментальнейшие из специальных
научных истин по их специальной науке, математике? Милые мои дети, мне тяжела
эта необходимость. Я ценю заслуги тех ученых, о которых ставлю такой
унизительный вопрос. Мне больно, что я должен поставить его. Но я должен. И материалом
для ответа на него я имею статью Гельмгольца "О происхождении и значении
геометрических аксиом". Я знаю ее разумеется, лишь по русскому переводу.
Он помещен в журнале "Знание" за 1876 год, №8,- я буду цитировать
перевод буквально.
Первые строки статьи: "Задачею настоящей
статьи является обсуждение философского значения новейших изысканий в области
геометрических аксиом и обсуждение возможности создания аналитическим путем
новых систем геометрии с иными аксиомами, чем у Эвклида". Это говорит г.
Гельмгольц, один из величайших -- это я знаю -- натуралистов и - читал я,
охотно верю, сам по этой его статье отчасти вижу -- один из самых лучших
математиков нашего времени. Все в этой статье я совершенно ясно понимаю. И я
говорю: он,- он, автор - он не понимает, о чем он говорит в ней и что он
говорит в ней. Он перепутывает математические термины и в путанице их
запутывает свои мысли так, что у него в голове сформировалась совершенно
бессмысленная чепуха, которую он и излагает в этой статье. Я буду поправлять
его ошибки в употреблении терминов, и техническая часть его статьи получит при
этих поправках правильный смысл. Без них в ней сплошная бессмыслица. Заметим
одно словечко в тех первых строках статьи. Гельмгольц хочет обсудить
философское значение предмета статьи. "Философское".- А в
"философии" он ничего не смыслит. В этом-то и причина падения его в
бессмыслицу. Он вычитал где-то что-то такое, чего не понял. Мы увидим, где и
что он вычитал. Но это увидим мы. Сам он этого не знает. […]
Дело у нас лишь в словах. А
Гельмгольц,- на этом,- на этом сбился, бедняжка. Он и какие-то, не помню в эту
минуту, но после найдем, какие именно,- он и какие-то другие
"новейшие" мастера рисовать формулы успели нарисовать какие-то
уравнения каких-то линий, о которых воображается им, что эти их
"открытия" очень важны. Так ли? Открытия ли это?- Я полагаю: это
мелочи, которых не вписали в свои трактаты и статьи Эйлер или Лагранж,
собственно, лишь потому, что пожалели - бумаги и времени писать такие пустые и
очевидные даже для меня решения пустяков. Вы лучше меня можете рассудить, так
ли,- но так ли, не так ли, мои милые друзья,- для сущности дела все равно.
Пусть эти "открытия" Гельмгольца с компанией действительно
"открытия", и притом даже "великие"; какой же убыток от
этих "открытий" аксиомам Эвклида? - Никакого, разумеется. […]
Пусть геометрия
совершенствуется; это прекрасно; но ровно ничего несогласного с
"Эвклидом" в ней не только теперь нет, но и никогда не будет. Так,
никакое развитие математики вообще не внесет в математику вообще ровно ничего
несогласного с правилами сложения и вычитания, и - спустимся еще ниже по
лестнице знаний - ничего несогласного даже с арифметикой дикарей, умеющих
считать только до трех. Неужели Гельмгольц не знает этого? - Сбился,
зафилософствавшись; вот и весь его грех; только. Так. Он лишь сбился. Но каково
же он сбился-то, это курьез. Нашел он с компанией какие-то - по-моему,
пустяки,- по его мнению, великие открытия. Пусть великие открытия. Нашел их и -
вообразил: найдены "новые системы геометрии", не согласные с
"Эвклидом". Вот до чего доводит "обсуждение философского
значения", когда пустится философствовать человек, ни уха, ни рыла не
смыслящий в философии. И надобно отдать справедливость этим "новым
системам геометрии": в них такие новости, что читать приятно.[…]
Это не факт, что пространство
имеет три измерения,- это лишь так кажется нам! Это не природа вещей иметь три
измерения,- это лишь иллюзия, производимая плохим устройством наших чувств! Мы
в этом отношении лишь "слепорожденные"! Милые мои друзья, возможно ли
человеку, находящемуся в здравом рассудке, иметь такую нелепую белиберду в
голове? - Пока он не "философствует", невозможно. Но если он, не
будучи подготовлен к пониманию и оценке философии Канта, пустится
философствовать во вкусе - он полагает - Канта, то всякая бессмыслица может
образоваться в его голове от возникновения в этой его бедненькой голове
комбинации слов, смысл которых не ясен ему. И, не понимая, о чем и что думает
он, может он воображать всякую такую бессмыслицу глубокомысленною
премудростью.[…]
Я рад был бы свалить всю вину
глупости на Гельмгольца, предположивши, что он вложил сам дикую фантазию свою в
работы Бельтрами, имевшие лишь дельную, разумную цель найти формулы для тех
поверхностей: кольцеобразной, двуседловидной и бокалообразной. Важны ли, не
важны ли эти формулы, новы ли они, или не новы в науке,- было бы все равно: цель работ, - дельная; и если автор доискивался решений, уж
данных другими, лишь неизвестных ему, это могло бы оказаться лишь случайным его
незнанием, и я рад признавать все такие случаи извинительными. Но - нет! - Бельтрами сочинял "не-Эвклидову
геометрию",- он сам; не Гельмгольц
вложил в его работы эту невежественную фантазию; он сам хвалится: он изобрел
новую геометрию. И не Гельмгольц вложил в его работы нелепое перепутывание
понятий "линия" и "поверхность" с понятием
"пространство"; нет, он сам говорит о "кривых
пространствах"; - о, урод!
Гельмгольц нашел, впрочем, что Бельтрами имел предшественника. Этот предтеча
сочинителя "кривых пространств", бывший профессором в Казани, некто
Лобачевский {1}. Еще в 1829 г., говорит Гельмгольц, "была составлена
Лобачевским система геометрии", которая "исключала аксиому
параллельных линий;- и тогда еще было вполне доказано, что эта система столь же
состоятельна, как и Эвклидова". И система Лобачевского "вполне
согласуется" с новою геометриею Бельтрами... Что такое "геометрия без
аксиомы параллельных линий"?»
Оба отрывка принадлежат перу одного человека: Николая
Гавриловича Чернышевского.
Первым, который является отрывком из известного романа
«Что делать?», упорно мучили многие поколения советских школьников, заставляя
учить его даже наизусть, вторым в виде фрагмента письма сам Чернышевский мучил своих
детей Сашу и Мишу.
Трудная судьба становления неэвклидовой геометрии являет
собой довольно типичную картину того, как сознание людское, а именно сознание тех немногих медиаторов-посредников, как
правило относимых в русском социуме к т.н. «интеллигенции», поступает с тем,
что оно осмыслить не в состоянии, но
может лишь представить и это
представление донести-передать другим, для которых даже чувственно представление
являет собой проблему и может восприниматься лишь непосредственное:
Итак, что же такое геометрия Лобачевского?
«Ответ, конечно, всем известен: это - геометрия, полученная из геометрии
Евклида изменением одной только аксиомы параллельных ("Геометрия
6-8", п. 33). Именно, у Лобачевского принимается за аксиому, что через
точку, не лежащую на данной прямой, проходит по крайней мере две прямые, параллельные
данной (то есть лежащие с ней в одной плоскости и ее не пересекающие).
Утверждения, или, другими словами, теоремы, которые выводятся из так измененных
оснований геометрии Евклида, и образуют геометрию Лобачевского.
Все это, как мы видим, "очень просто" и говорится коротко и
ясно. Трудность, однако,
в том, что аксиома Лобачевского не соответствует нашему наглядному
представлению. Поэтому и выводы из нее - многие теоремы геометрии Лобачевского
- оказываются вовсе странными и невообразимыми. Реальный смысл
этой геометрии из данного выше ее простого формального определения совершенно
не ясен».
Какая
же связь между неопределимым и манящим ароматом непредставимости и
невообразимости неэвклидовой геометрии, например, геометрии Лобачевского и специфическим
запахом казармености социалистических устремлений как в их
истоке (на примере чернышевский снов о светлом будущем), так и в самих «социалистических»
снах ставших реальностью т.н. «развитого социализма»?
Каждому представителю
вида хомо сапиенс ведь должно быть понятно, что именно стерло с мировой
политической карты мира «систему мирового социализма». Вовсе не усердие сотен и
сотен миллионов западных представителей «свободного мира», желающих защитить
свою насквозь животную свободу потреблять, потреблять и потреблять, а простое нежелание далее мириться с казарменной
вонью обитателей самих «социалистических» казарм.
N:
… Социализм… Чернышевский видит его в виде гигантской казармы-общежития,
не лишенная правда некоего абстрактно-утилитарного изящества на фоне нетронутой,
но облагороженной цивилизованностью природы…
… Единство, но единство как совершенно недифференцированной
рабочей массы… Причём явно кем-то хорошо организованной… И такая удивительная, почти необъяснимая тяга к
«кормлению больших масс людей»… Хотя пища видимо добротная
и её достаточно и всё, конечно же, с «песней по жизни», одним словом с одним словом…
И это слово такое странное, ибо слово это «социализм»…
Но каковы медиаторы – таков и … социализм.
Ведь Будущее может быть познано лишь как понятие и на уровне
понятия, а для этого нужно уметь мыслить и уметь видеть глазами разума.
Не будем просто критиковать
Чернышевского, он сделал то, что мог сделать и дорого заплатил за это. Другие
не смогли сделать и сотой части подобного, но проблема понимания и разумения
того, что должно пониматься, а не представляться
понятым остаётся.
И когда разума недостаточно,
в дело включается его формальный заместитель и тогда появляются оценки, за
которые придётся отвечать. Гений – не сумасшедший,
хотя в глазах тех кто не может в принципе сойти
с ума, так как ещё не знает, что это такое, и не имеет ни единой своей
мысли, как правило выглядит таковым.
Очень легко упрекнуть такого
«философа», как Чернышевский, и к тому же философа так … исключительно хорошо разбирающегося в геометрии, в грехе простого невежества и самонадеянности. Но осознаем полностью ситуацию, дело ведь в
том, что предмет социальной науки, за которую так смело взялся
Чернышевский и с удовольствием берется любой интеллигент ныне, существенно сложнее банальностей
неэвклидовой геометрии, в которой логика
геометрического пространства входит в противоречие с логикой непосредственного
здравомыслия формального восприятия.
Категории-понятия «класса»,
«стоимости», «государства», да и, например, самого сакраментального
понятия «социализм» («коммунизм») уже настолько оторваны от любого материально-вещественного носителя, и настолько непредставимы и лишены субстанции
чувственного восприятия, что любая самая невинная попытка формализации и
вульгаризации понятия превращает пытающегося
такое сделать в безумствующую бестолочь.
Безумствующей бестолочью и были все те, кто брался за задачу
социального проектирования и прогнозирования, что собственно и составляет
основу сложнейшей задачи социальной революции, так и не сумев осмыслить предмет, то есть выразить его в понятиях и прежде всего понимать, что означает понимать.
Из сказанного конечно же
совершенно не следует, что за подобного рода задачи не нужно браться.
Конечно, нужно. Необходимо, как вообще необходимо учиться мыслить, но чтобы
учиться мыслить нужно осознать,
что из мыслительной активности, которая делает человечка человеком, пока
самому мыслителю недоступно.
Ясно, что для Чернышевского, да и любого
здравомыслящего человека далекого от парадоксов проективной геометрии
утверждение вида «точки находятся по разные стороны, но при этом точки
находятся по одну сторону», утверждения которое кажется совершенно несовместимо
ни с каким здравым представлением и реальностью, не может удовлетворить и
вызовет лишь праведный гнев. Но мы уже знаем, знаем на примере «кольца
Мёбиуса», что формальная логика в данном
случае даёт осечку и что ситуация парадокса одновременности реализации указанных
противоречивых утверждений – это простая реальность, легко проверяемой и
наглядной банальности указанного кольца как упрощенной модели так называемой проективной плоскости.
Формальная логика при определенных условиях становится
аформальной, а при известных условиях обе логики могут превращаться, переходить
друг в друга являя таким образом логику
трансформального. Математическая сфера в этом отношении может научить
многому, так как в упрощенной форме даёт как бы мог выразиться сам А.Ф.Лосев
наглядную модель алогического становления новой логики, логики дающей ключ к
пониманию путей законного трансформирования самого сложного с чем может иметь
дело человек намеревающийся изменить мир – мир
социальных форм.
А творимое человеком в
соответствии с Законом – уже неподвластно тому, что всегда и неизменно превращает
в руины творения человеческие, делая их временным и подверженным тлению и
разрушению. Ведь человек как действующий
исторический субъект, действующий совместно с Законом, един с Ним и
неотличим от самого Закона, и этим являет Волю Всеобщего, которой является
Закон. Понятно, что речь идёт о любом
человеке и проблема человека и вообще человечности
как таковой лишь в неосознанности или осознанности самого действия.
Законность – это полная
осознанность.
Неудивительно, что Всеобщее так нечеловечески
и сверхчеловечески немилосердно к человечности, так яро стирает одни
формы, чтобы создать новые, но кажется с единственной целью - так же стереть последние
с лица Планеты. И за этой яростью торжества всеобщей вакханалии зла
перманентного уничтожения лишь самый внимательный и осмысленный человеческий взгляд
способен узреть и понять истину творящегося – Всеобщее-Творец с возрастающей
силой требует от Своих творений лишь одного – полной осознанности, что и
есть заповеданное в Священных Писаниях Образ и Подобие Творения – Творцу
Своему.
«Сам Лобачевский называл свою геометрию воображаемой. Он смотрел на нее
как на теорию, которая могла бы оказаться приложимой к реальному пространству.
Но только "могла бы" - реальных же приложений не было. Поэтому и
логическая непротиворечивость этой геометрии оставалась не установленной. Ведь
как ни развивал ее Лобачевский, а могло бы оказаться, что дальше все-таки
обнаружится противоречие.
Реальный смысл и логическая непротиворечивость геометрии Лобачевского
вытекают из ее простой модели, придуманной немецким математиком Ф. Клейном. Вот
эта модель.
За "плоскость" принимается внутренность какого-либо круга
(рис. 1), за "точки" - точки этой внутренности, за "прямые"
- хорды - конечно, с исключением концов,
поскольку рассматривается только внутренность круга. За "перемещения"
принимаются преобразования круга, переводящие его в себя и хорды - в хорды.
Соответственно, "конгруэнтными" называются фигуры, переводимые друг в
друга такими преобразованиями.
Всякая теорема планиметрии Лобачевского является в этой модели теоремой
геометрии Евклида и, обратно, всякая теорема геометрии Евклида, говорящая о
фигурах внутри данного круга, является теоремой геометрии Лобачевского. Это
общее утверждение доказывается проверкой справедливости в модели аксиом
геометрии Лобачевского.
То, что аксиома параллельных не выполняется в этой модели, видно
непосредственно: на рисунке 2 через точку С, не лежащую на "прямой"
(то есть на хорде) АВ, проходит бесконечно много "прямых" (хорд), не
пересекающих (АВ).
Поэтому, если в геометрии Лобачевского имеется противоречие, то это же
противоречие (вернее, его перевод на "язык в круге") имеется и в
геометрии Евклида.
Далее, всякая теорема геометрии Лобачевского описывает в модели Клейна
некоторые факты, имеющие место внутри круга. Именно факты, если мы берем не
абстрактный круг, а реальный круг и реальные хорды И понимаем теоремы как
утверждения об этих реальных вещах, взятые, конечно, с той точностью, которая
доступна для наших построений. Таким образом, геометрия Лобачевского имеет
вполне реальный смысл с той точностью, с какой вообще имеет смысл геометрия в
применении к реальным телам.
Стадо быть, геометрия Лобачевского настолько непротиворечива, насколько
непротиворечива геометрия Евклида, и имеет в такой же степени реальный,
экспериментально устанавливаемый смысл. […]
Из довольно многочисленных (55) появившихся в 18 в. сочинений по теории
параллельных особенно выделяется написанная в 1766 г. "Теория
параллельных" И. Г. Ламберта, немецкого математика, физика и астронома.
Ведя доказательство пятого постулата от противного, Ламберт вывел из его
отрицания много следствий. Он, можно сказать, в значительной мере построил
основы геометрии Лобачевского. В его выводах не было противоречия, и он не
подумал, что нашел его, как это делали почти все его предшественники. Ламберт
даже высказал мысль, что он "почти должен сделать вывод", что
опровергаемая им гипотеза "имеет место на какой-то мнимой сфере". Но
все же он остался уверен, что геометрия, основанная на отрицании пятого
постулата, невозможна. Его работа не давала, однако, доказательства этому
убеждению. Поэтому, надо думать, он остался ею недоволен и не опубликовал ее.
Она была издана только в 1786 г. - через 9 лет после его смерти и через 20 лет
после того, как она была написана. В общем Ламберт очень близко подошел к
открытию новой геометрии, но не сделал его.[…]
Гаусс, по его собственному свидетельству, занимался теорией параллельных
с 1792 г. и, как видно из его переписки, постепенно приходил к убеждению, что
доказательство пятого постулата невозможно. Так, в 1817 г. в письме к Ольберсу
он писал:
"Я прихожу все более к убеждению, что необходимость нашей геометрии
не может быть доказана, по крайней мере человеческим рассудком и для
человеческого рассудка".
[…] … только в 1831 г. он взялся за то, чтобы изложить, хотя бы кратко,
свои выводы, но за всю свою жизнь так ничего и не опубликовал по поводу
неевклидовой геометрии. В 1829 г. в письме к Бесселю он писал: "Я опасаюсь
крика беотийцев, если выскажу мои воззрения...". Он боялся подорвать свой
научный авторитет.
Беотийцы,
жители области Древней Греции Беотии, считались особо глупыми, так что название
"беотиец" было нарицательным.
Но когда Гаусс писал все это, уже нашелся человек, который не только
совершенно удовлетворительно развил геометрию, отрицающую пятый постулат, и не
только пришел к убеждению, что эта геометрия совершенно последовательна, но, не
убоявшись ничьего крика, доложил все это научному собранию. Это был Николай
Иванович Лобачевский, который пришел к убеждению о возможности неевклидовой
геометрии еще в 1824 г. и представил доклад с изложением ее начал
физико-математическому факультету Казанского университета 23 (11) февраля 1826
года; опубликовал он его в расширенном виде в работе "О началах
геометрии" в ряде выпусков "Казанского вестника", научного
издания Казанского университета, с февраля 1829 по август 1830 г.
В 1835-38 гг. Лобачевский публикует более развитое изложение своей
теории "Новые начала геометрии с полной теорией параллельных", в
предисловии к которому пишет:
"Напрасное старание со времен Евклида, в продолжении двух тысяч
лет, заставило меня подозревать, что в самих понятиях еще не заключается той
истины, которую хотели доказывать и которую проверить, подобно другим
физическим законам, могут лишь опыты, каковы, например, астрономические
наблюдения". […]
Как история пятого постулата и неевклидовой геометрии демонстрирует
человеческий гений, так демонстрирует она и неповоротливость ума, если избегать
грубого слова "тупость".
Начать с того, что множество попыток доказать пятый постулат было
основано на ошибках. Авторам этих доказательств только казалось, что они нашли
доказательство. Так было даже в начале XIX века. […]
И Ламберт, далеко развивший неевклидову геометрию, только
"почти" сделал вывод о ее выполнимости, и Гаусс мучительно долго
"все более приходил" к убеждению о невозможности доказать пятый
постулат.
Когда же неевклидова геометрия
была открыта и обнародована и встал вопрос о ее реальном смысле, то тут
несообразительность показала себя в полную силу.
Гаусс еще в 1827 г. развил основы общей теории геометрии на
поверхностях, в которой роль прямолинейных отрезков играют кратчайшие линии,
расположенные на поверхности. У него был получен, в частности, вывод, что на
некоторых поверхностях (поверхностях отрицательной кривизны) сумма углов
треугольника (стороны которого кратчайшие линии) меньше 180°. Он знал вместе с
тем, что в неевклидовой геометрии верно то же. Но он не сопоставил эти два
вывода, не догадался, что неевклидова геометрия должна осуществляться на
некоторых поверхностях. Если бы он додумался до этого, то доказательство не
представляло бы для него, при его исключительной силе математика, особого труда
(этот вывод был получен итальянским математиком Бельтрами только 40 лет
спустя). […]
И только в 1871 году Клейн делает это сопоставление - приходит к той
простой модели в круге, о которой мы рассказали вначале. Указанием на эту
элементарную модель решается вопрос о недоказуемости пятого постулата. Вот к
чему, можно сказать, свелось то, над чем более 2000 лет бились умы математиков!
История неевклидовой геометрии показывает, с каким трудом люди доходят
до вещей, которые, когда они наконец ухвачены и понятны, оказываются простыми,
и как люди зачастую не понимают, что делают и что лежит у них под руками. Ни
Гаусс, ни Лобачевский не поняли то, что было у них почти в руках. Даже Гаусс и Лобачевский.
В наше время все еще находятся
люди, занимающиеся "доказательством" пятого постулата и осаждающие
математиков этими своими "трудами". Но так как вопрос о пятом
постулате решен и решение это с помощью модели в круге нетрудно понять каждому,
названные "доказательства" и "труды" относятся уже не к
неповоротливости ума, а к глупости или даже к сфере медицины. Глупость - это
совсем не то, что тупость - неповоротливость ума; напротив, у дурака может быть
"легкость в мыслях необыкновенная", ум его может поворачиваться с
головокружительной быстротою, да бестолку. Это не имеет никакого отношения к
той неповоротливости ума, свойственной даже гениям, которую так ярко показывает
трудная история пятого постулата и неевклидовой геометрии. […]
Талант, гений - это не только специальные способности, но и характер.
Как Магеллану и Нансену была нужна решимость, чтобы отправиться в неизведанное
плавание, так теоретику нужна интеллектуальная решимость, чтобы подумать
"невероятное" и развивать его вопреки не только устоявшимся взглядам
и традициям, но нередко и вопреки собственным сомнениям. Но мало убедиться в
своих идеях для самого себя - их нужно передать другим людям. А это тоже может
требовать решимости, потому что люди могут не понять, отбросить и даже
подвергнуть насмешкам и поруганию новые идеи и выводы. Это могут сделать в
первую очередь свои же коллеги - ученые, убежденные в незыблемости своих
взглядов в своей академической непогрешимости, - мещане в академических креслах
и на профессорских кафедрах, те "беотийцы", которым побоялся
противопоставить себя Гаусс.
… Гауссу ничего не грозило, кроме разве нелестных суждений коллег, а он
скрыл свои научные убеждения, скрыл истину. Он поступил мудро с точки зрения
мещанства, одинаково - прошлого или современного, подвизающегося в науке или
всякого другого.».
Как уже было сказано, мы не ставим себе целью дать
более или менее полное освещение рассматриваемой темы и предмета, но лишь наглядно показать пути, которые при желании могут
позволить всякому развитому формальному
мышлению своим собственным развитием и усилиями перейти на следующую
интеллектуальную ступень. И в этом (безусловно, нелегком деле) овладение
основами проективной геометрии может очень существенно помочь познающему
субъекту.
По указанным
причинам нет ничего удивительного в том, что мы, как правило, используем самый
доступные для понимания учебные источники и материалы, в самом простом и популярном изложении.
Не
исключение и источник, который мы будем рассматривать далее.
Итак, научно популярная серия «Мир знаний», «От
проективной геометрии — к неевклидовой (вокруг абсолюта).
Одной из дополнительных причин, которые делают
необходимым избрать именно эту небольшую брошюру является её название, которое
в явной и совершенно отчетливой форме показывает то, вокруг чего всё происходит - показывает абсолют. И хоть абсолют этот во многом всё же формальный, но
сам факт ясного выявления основания, центра математической формы очень привлекает.
Мы помним, что
простой моделью предложенной хорошо нам знакомым Феликсом Клейном, которая
показывает, как именно формально
реализуется геометрия Лобачевского, является довольно маловразумительная
картинка круга, внутри которого находятся некие «прямые» и «точки»:

Что это за круг, почему граница круга обозначена
пунктиром и по всей видимости ещё многие иные «почему?» требуют ответа.
Раз требуют – начнём отвечать.
«Значение открытия Николая
Ивановича Лобачевского общеизвестно и сущность его широко освещена в популярной
литературе. В результате у значительной части читателей создалось впечатление,
что решение проблемы пятого постулата является высшим достижением и последним
словом геометрии, что все основные задачи этой науки решены, что геометры в наше
время занимаются лишь какими-то частными и незначительными вопросами.
В действительности дело обстоит далеко не так. Более того, именно с
появлением новой геометрии открылись совершенно новые горизонты в развитии
одной из древнейших наук и началось активное проникновение геометрии не только
во все разделы современной математики, но и во многие области физики.
В эволюции идей Лобачевского и создании современной геометрии решающую
роль сыграло возникновение проективной и дифференциальной геометрий. Однако ни
проективная, ни дифференциальная геометрии не получили в отечественной
популярной литературе достаточного освещения. В предлагаемой книге излагается
история развития и некоторые факты проективной геометрии. Но главная цель книги
не в этом.
Проективная геометрия является наиболее удобным исходным пунктом для
объяснения сущности не только геометрии Лобачевского, но и широкого круга
других геометрических систем, возникновение которых связано с именем Феликса
Клейна, с идеями теории групп преобразований. Именно, при помощи методов
проективной геометрии, обходясь относительно простым математическим аппаратом,
можно описать девять хорошо известных в науке неевклидовых геометрий плоскости
и показать возможность их применения в физике. Решающую роль в таком описании
играет понятие абсолюта, т. е. некоторой фигуры, заданной на проективной
плоскости и остающейся неизменной при всех преобразованиях некоторой подгруппы
группы проективных преобразований. Рассказ об этом и составляет основное
содержание книги.
Возникновение нового всегда связано с творчеством выдающихся личностей.
Идеи, о которых пойдет речь, связаны с именами Леонардо да Винчи, Дезарга и
Паскаля, Понселе и Шаля, Штейнера, Мёбиуса и Штаудта, Клейна, Гильберта и
Минковского, К.А.Андреева и Н.А. Глаголева. Познакомить читателей с жизнью и
творчеством этих замечательных людей — еще одна цель книги».
Очень интересное, простое и поучительное наблюдение.
Параллельные прямые при непосредственном (пространственном) восприятии
человеком мира всегда пересекаются в
одной точке, причём, если таковое отсутствует, прямые не воспринимаются как
параллельные.
И это правда. Несомненно
параллельные друг другу рельсы сходятся в точку на горизонте. В любом
живописном полотне которое призвано показывать зрителю объем, пространство должно
строиться по закону перспективы, научные основы которой заложил гениальный
Леонардо да Винчи:
«Леонардо не был первым из тех,
кто понял значение перспективы, значение геометрии для живописи. Но он сумел
наиболее четко и выразительно сформулировать основные идеи теории перспективы,
определить ее значение для практики живописца, архитектора, инженера и оставить
примеры гениального применения этих идей не только в «Тайной вечере».
Теорию перспективы Леонардо рассматривает как порождение науки живописи.
Уже само словосочетание «наука живописи» полно глубокого смысла. Оно
показывает, что живопись имеет в своей основе строго научные закономерности,
связанные с закономерностями человеческого зрения. «Мы знаем, что точка зрения
помещается в глазу зрителя сюжета» — этой фразой начинается у Леонардо его
теория перспективы.
Попытаемся уточнить формулировку задачи, стоявшей перед великим
художником. Необходимо, чтобы изображение производило на зрителя такое же
впечатление, что и изображаемый предмет. Как же возникает это впечатление? Из
каждой видимой точки предмета луч света попадает в глаз зрителю, преломляется в
зрачке, попадает на сетчатку глаза, на сетчатке возникает изображение
рассматриваемого предмета. Дальнейшее (сетчатка, зрительный нерв, кора
головного мозга) изучается анатомией и физиологией.
Теперь представим себе, что между
глазом и предметом установлена прозрачная плоская пластинка. Каждый луч,
направленный от видимой точки к глазу, пересечет эту пластинку в одной точке.
Множество таких точек и даст изображение предмета на пластинке. Описанный
процесс носит название центрального проектирования, а полученное изображение
называется проекцией.
Такой проекцией в принципе должно быть и изображение предмета на любой
плоскости, заменяющей эту прозрачную пластинку, — будь то холст, или бумага,
или стена, отведенная для будущей фрески».

Вернемся к «Тайной вечере». Каждой видимой зрителю точке помещения, где
происходило изображенное событие, соответствует определенная точка на картине.
Каждому отрезку прямой (край стола, стороны окон и т.д.) в помещении
соответствует отрезок прямой и на фреске. При этом равные отрезки не всегда
изображаются на картине равными же отрезками, изменяются и некоторые углы.
Например, надо полагать — и нарисовано так, что в это веришь, — потолок в
комнате был прямоугольным, но его изображение на фреске имеет вид трапеции.
Наконец, самое важное. В оригинале линии, по которым стены пересекаются с
потолком, параллельны. На проекции соответствующие линии (точнее, их продолжения)
пересекаются в одной точке. Тот факт, что они пересекаются на изображении
головы Христа, делает его фигуру еще более значительной, центральной,
подчеркивающей особое место главного, героя картины...»
Теория перспективы в объеме необходимом для живописи
быстро была освоена художниками, но её неосознаваемые пока значимость для
многих иных сфер активности человека отложило дальнейшие исследование на многие десятилетия.
Первый шаг был сделан в 1639 году архитектором Жираром
Дезаргом 1591 — 1661).
«Дезарг решается на очень простой и именно в простоте своей и необычный
шаг: он предлагает считать эти точки пересечения изображениями (проекциями)
«бесконечно удаленных» точек, в которых «пересекаются» параллельные прямые
(рис. 2; точке Т' плоскости β соответствует бесконечно удаленная точка Т
плоскости α). Более того, он предлагает считать бесконечно удаленные точки
прямых равноправными (со всеми остальными) точками. Говоря более современным
языком, Дезарг дополняет евклидово пространство новыми элементами: несобственными
(бесконечно удаленными) точками, а также еще и плоскостью, на которой лежат все
несобственные точки, — несобственной плоскостью».
«Две прямые, лежащие в одной и той
же плоскости, у Евклида пересекаются, если они не параллельны. У Дезарга две
прямые одной плоскости всегда пересекаются. Ограничений никаких. Значит,
большая общность, значит, большая область применения, значит, новое
пространство охватывает «старое» евклидово примерно так же, как множество
рациональных чисел включает в себя множество чисел целых.
Это «дополненное» евклидово
пространство и служит хорошей моделью того нового пространства, которое ввел
Дезарг и которое в наше время называется проективным пространством. Геометрия
этого пространства, называется проективной геометрией, и будет основным
объектом нашего внимания в дальнейшем. Название «проективная»
подчеркивает, что идеи новой геометрии возникли при изучении операции
проектирования».
Следующим весьма интересным моментом развития
проективной геометрии является то, что на удивление у неё выявились русские
корни, и корни эти весьма своеобразны. Дело в том, что в особо рассматриваемом
нами 19-м столетии эстафета развития теории была подхвачена Жаном Виктором
Понселе, а свои проективные изыскания последний осуществлял в течение
пятнадцати месяцев в русском плену.
В чём заслуга Понселе?
«Понселе выделил «проективные»
свойства геометрических фигур и указал на замечательный инструмент их изучения,
порожденный внутренней структурой проективного пространства, — на «принцип двойственности».
Теперь стала ясной область исследования новой геометрии — проективные свойства
фигур».
Что такое принцип двойственности?
«…из каждого проективного предложения относительно
точек и прямых на плоскости может быть получено второе предложение путем замены
слова «точка» словом «прямая» и наоборот».
Видимо достаточно трудно оценить полностью глубину и
значение принципа двойственности, если не учитывать ещё некоторые важные
обстоятельства.
Воспользуемся ещё одним источником, который пожалуй наиболее наглядно показывает главную
особенность пространства проективной геометрии, заставляя преодолевать границу между
представлением и осмыслением:
«В элементарной геометрии вопрос о том, что такое пространство, равно
как и вопрос, что такое геометрическая фигура, вообще не возникает или, если
возникает, то сразу же получает разрешение: пространство воспринимается как
непосредственно данная, не требующая никакого пояснения, реальность; фигуры,
расположенные в пространстве—это хорошо всем известные треугольники, квадраты,
параллелепипеды и пирамиды, а также круги, цилиндры, шары и конусы. В этом
положении вещей принципиально ничего не меняется, когда запас изучаемых фигур
пополняется, как это делается в курсах высшей математики, привлечением ряда
новых линий и поверхностей.
Однако, при весьма простой операции проектирования одной плоскости на
другую, или одной данной прямой на другую из некоторого центра проекции,
наступает явление, заставляющее серьезно задуматься о природе изучаемого
геометрией пространства. Операция проектирования из точки О заключается, как
известно, в следующем. В данной точке O воображаем источник света, испускающий
лучи во всех направлениях. Одну из двух плоскостей мыслим в качестве бесконечно
простирающегося во все стороны прозрачного листа, на котором могут быть
нарисованы различные фигуры (как на пластинке для волшебного фонаря). Другую
плоскость мыслим в виде также бесконечно простирающегося во все стороны экрана.
Тогда луч света, исходящий из точки О и проходящий через какую-либо точку
стеклянного листа, отображает эту точку в некоторую точку экрана. Таким образом
каждой одной плоскости будет, вообще говоря,1 соответствовать одна единственная
точка другой плоскости: соответствующими друг другу являются точки наших двух
плоскостей, лежащие на одном и том же луче, исходящем из “центра проекции О”.
Это соответствие называется перспективным соответствием, а операция перехода от
какой-либо точки одной плоскости к соответствующей ей точке другой плоскости
называется проектированием этой точки (на определенную плоскость) из точки О.
Предположим, в частности, что наши две плоскости не параллельны друг
другу. Пусть на одной из них (“на пластинке”) нарисована окружность. Лучи,
идущие из О через точки этой окружности, образуют конус лучей с вершиной в О. В
зависимости от угла между нашими двумя плоскостями, окружность, лежащая на
одной из них, спроектируется на другую или в виде эллипса, или в виде параболы,
или, наконец, в виде гиперболы. Но окружность есть линия замкнутая, тогда как
парабола и обе ветви гиперболы не смыкаются нигде в конечной части плоскости.
Приходится признать одно из двух: или, что можно спроектировать замкнутую линию
в незамкнутую, или, что такие линии, как парабола и гипербола, в
действительности суть линии замкнутые, но что смыкаются они в
бесконечно-удаленных точках плоскости.
Второе допущение было сделано свыше ста лет тому назад знаменитым
французским геометром Понселе (Poncelet). Понселе предположил, что на плоскости
существует бесконечно много бесконечно-удаленных точек, образующих так
называемую бесконечно-удаленную прямую, с которой всякая прямая пересекается в
единственной точке, в своей бесконечно-удаленной точке. Таким образом из
допущения Понселе в частности следует существование
одной бесконечно-удаленной точки на каждой прямой; следует также и то, что и прямая есть замкнутая линия (смыкающаяся в
своей бесконечно-удаленной точке). Кроме того, две
прямые тогда и только тогда имеют одну и ту же бесконечно-удаленную точку, если
они – параллельны».
«Приходится
признать одно из двух: или, что можно спроектировать замкнутую линию в
незамкнутую, или, что такие линии, как парабола и гипербола, в действительности
суть линии замкнутые, но что смыкаются они в бесконечно-удаленных точках
плоскости».
Итак, во-первых, именно формальная
логика позволяет сделать вывод о том, что проекции окружности (парабола и
гипербола) также являются замкнутыми геометрическими формами.
«… из
допущения Понселе в частности следует существование одной бесконечно-удаленной
точки на каждой прямой;»
Во-вторых, (хочется даже с некоторой
иронией добавить «как ни удивительно») сама логика самоопределения понятия
«прямой», как «неограниченно простирающейся линии обладающей качеством
прямизны» и по этой причине, очевидно, всё же не являющейся конечным отрезком, предполагает
существование таких точек прямой (на прямой) которые бесконечно удалены от данной точки.
«…из допущения Понселе в
частности… следует также и то, что и
прямая есть замкнутая линия (смыкающаяся в своей бесконечно-удаленной точке).
В-третьих, и этот вывод особо для нас значим, любая
прямая – замкнута и являет собой, если как-то представить указанное «смыкание в
своей бесконечно-удаленной точке», бесконечное кольцо, фрагмент которого в
силу осуществления формального определения носит наименование «прямой».
«Кроме того, две прямые тогда и
только тогда имеют одну и ту же бесконечно-удаленную точку, если они –
параллельны»
И, наконец, в-четвертых,
формальная параллельность двух прямых как отсутствие у них – формальное
требование!- общей точки имеет
необходимое основание в виде наличия в бесконечности такой точки.
Без второго – не может быть
первого.
Таким образом, именно
появление аформальности (бесконечности, охватываемой как некоторое целое), так
называемых «бесконечно удаленных элементов» является по сути обретением аформального основания.
Логика существования такого
основания, являющегося необходимым
основанием любой формы диктует-и-определяет
логику существования формальных форм, которые определяются через существование
(движение) аформальных форм, которые в свою очередь также самоопределяются
своим-иным, т.е. формальным.
Теперь мы уже, видимо, можем
отдать должное принципу двойственности, сущность которого – вовсе не провозглашаемая
формальная «двойственность», а напротив – единство и неразличимость в
проективном пространстве любых отношений двух форм: точки и прямой, что не может не означать сущностное
единство обоих, которое легко можно увидеть в единой универсальной т-форме,
форме кольца.
Иными словами, в разумозрительном отношении «принцип двойственности» в проективной геометрии означает уже нам хорошо известное:
А) Относительно
необходимого аформального основания точка тождественна прямой, т.е. бесконечно малое кольцо это точка, а бесконечно
большое кольцо (абстрактно-формальный
«фрагмент») – это прямая.
Б) любая бесконечная
прямая замкнута на саму себя и потому
бесконечна и несёт в качестве своего необходимого основания своё
противоположное (выражаясь строго математически
аналитически) – замкнутую кривую второго
порядка;
И если просто не
формализовать аформальное и затем рассматривать противоположные формы как
простую формальную двойственность и абстрактные и независимые друг от друга
первичные геометрические формы,
т.е. сделать следующий шаг от формального к аформальному, речь, разумеется о трансформизации понятий:
В) точка и
прямая порождаются друг другом своим собственным движением через самих себя.
Итак, именно та или иная форма формализация геометрической аформальности, появившейся в математике (геометрии), к слову совершенно неизбежная и даже
необходимая, выявившаяся в 19 столетии,
породила целый спектр математических форм, в которых в той или иной мере такая
аформальность имела место в явном или неявном виде.
Дело в том, что
видоизменение математического основания (та или иная форма его аформализации)
неизбежно и сразу ведёт к изменению формально-аксиоматического основания математической
дисциплины.
Неэвклидова геометрия формально
ни в малейшей мере не содержит в себе явного присутствия бесконечности.
Бесконечное скрыто и даже намертво вмуровано в аксиоматике пятого постулата эвклидовой геометрии,
которая по этой причине видится именно и
только как отношение формальных базовых
аксиоматических форм, логика отношений которых строго соответствует формальной
логике непосредственно-чувственного восприятия.
«Прямая» («плоскость») - это
некая абстракция, причём фактически и
логически формально нереализуемая – невозможно изобразить бесконечную прямую
(плоскость), изображая прямую тот,
кто занимается таким делом, изображает обязательно формальную, оконеченную
модель прямой (плоскости) и далее оперирует с ней, но оперирует уже как с
«настоящей» прямой(плоскостью).
Аформальное, бесконечное не привносится
откуда-то и не является чем-то чуждым форме и определенности всякой формы.
Проективная геометрия, например, возникает из формального осмысления
непосредственного – чувственного восприятия того, что параллельные прямые сближаются, сходятся, если наблюдать указанную картину на «больших расстояниях»,
и как логическое следствие – формулировки вполне закономерного вопроса: «А не
пересекаются ли эти параллельные прямые в бесконечности?»
Аформальное рождается в процессе отношения и взаимодействия самих форм, а рождаясь, неизбежно
делает подвижными и изменчивыми формальные т.е. аксиоматические основания, что в свою очередь соответственным образом видоизменяет сами формы и их
отношения, которые вырастают из таких аксиоматических
мутаций.
Неэвклидова геометрия
появлялась на свет как некоторое осмысление, но именно формальное осмысления
чисто формальной возможности существования иных, чем виделось
самим математикам определений и отношений математических (геометрических) форм
и их непротиворечивости, по крайней мере в той мере в какой была непротиворечивой
сама эвклидова геометрия, из которой проклёвывался цыпленок неэвклидовости:
«Мысль о том, что в основу фактического построения геометрии могут быть
положены не только точки, но и другие элементы, в первую очередь прямые, а
затем и гораздо более сложные образы, с необходимостью возникла при построении
проективной геометрии, то есть свыше ста лет тому назад; она получила свое
дальнейшее развитие в середине прошлого века в работах Плюккера (Plucker) и
Клейна (Klein) и в настоящее время является одной из неотъемлемых основных
частей геометрического мышления.
Если одни и те же соотношения господствуют в двух различных системах
элементов, то мы говорим об одной геометрии, а не о двух разных: так, например,
мы отождествляем геометрию проективной плоскости с геометрией связки лучей.
Но если рассматривать две разные системы соотношений, хотя бы в одной и
той же системе пространственных элементов, то мы получим две различные
геометрии. Первым по времени и наиболее важным примером этого рода наука
обязана неэвклидовой геометрии, возникшей приблизительно одновременно с
проективной в трудах великого русского геометра Н. И. Лобачевского и некоторых
его современников. Суть неэвклидовой геометрии заключается в том, что система
основных пространственных элементов начальной геометрии — точек, прямых,
плоскостей — в неэвклидовой геометрии предполагается удовлетворяющей иной
системе основных соотношений (аксиом), чем в обычной, эвклидовой геометрии.
Конкретно, в геометрии Лобачевского предполагается, что в данной плоскости к
данной прямой через не принадлежащую к этой прямой точку можно провести более
одной параллельной прямой. Это изменение в основных соотношениях (аксиомах)
влечет за собою, конечно, изменение и в остальных соотношениях между
пространственными элементами, соотношениях, составляющих содержание данной
геометрии. Так, например, в геометрии Лобачевского сумма углов треугольника
меньше двух прямых, в ней не существует прямоугольников; всякие две подобные
фигуры в геометрии Лобачевского необходимо равны между собою и т. д. Словом,
получается геометрическая картина, резко отличающаяся от привычной нам
геометрии Эвклида.
Естественно возникает тот же вопрос, который мы уже ставили по поводу
проективной геометрии, а именно, вопрос о реальности, о фактическом смысле
неэвклидовой геометрии. Из этого вопроса современники Лобачевского так и не
могли выпутаться, и в этом, в основном, и заключается, конечно причина
непризнания идей Лобачевского со стороны большинства даже и крупных математиков
его времени (например Остроградского)».
Обратим внимание:
«Суть
неэвклидовой геометрии заключается в том, что система основных пространственных
элементов начальной геометрии — точек, прямых, плоскостей — в неэвклидовой
геометрии предполагается удовлетворяющей иной системе основных соотношений
(аксиом), чем в обычной, эвклидовой геометрии. Конкретно, в геометрии Лобачевского
предполагается, что в данной плоскости к данной прямой через не принадлежащую к
этой прямой точку можно провести более одной параллельной прямой».
Но суть неэвклидовой
геометрии вовсе не в этом, уж по
крайней мере не в том, чтобы ученые-геометры хоть в чём-то уподобились
персонажам из романа Дюма «Графиня Де Монсоро»:
«… мне страшно хочется съесть эту курицу и в то же время не согрешить.
Послушайте, брат мой, сделайте милость - во имя нашей взаимной любви окропите
ее несколькими капельками воды и нареките карпом.
- Чур меня! Чур! - заохал монах.
- Я вас очень прошу, иначе я могу оскоромиться и впасть в смертный грех.
- Ну ладно, так и быть, - сдался Горанфло, который по природе своей был
хорошим товарищем, и, кроме того, на нем уже сказывались вышеописанные три
дегустации, - однако у нас нет воды.
- Я не помню где, но было сказано, - заявил Шико. - "В случае
необходимости ты возьмешь то, что найдется под рукой". Цель оправдывает
средства; окрестите курицу вином, брат мой, окрестите вином; может быть, она от
этого станет чуточку менее католической, но вкус ее но пострадает.
И Шико опорожнил первую бутылку, наполнив до краев стакан монаха.
- Во имя Бахуса, Мома и Кома, троицы великого святого Пантагрюэля, -
произнес Горанфло, - нарекаю тебя карпом».
«Модель Пуанкаре — это одна из возможных евклидовых моделей геометрии
Лобачевского. * Что представляет собой
такая модель? Это конкретная небольшая часть геометрии Евклида, в которой
выделены специальные понятия, играющие роль основных понятий геометрии Лобачевского
— таких, как точка, прямая, перемещение и т. п. Выделенные понятия выбираются с
таким расчетом, чтобы для них выполнялись все основные положения (аксиомы)
геометрии Лобачевского.
- Как такое может быть? — спросит читатель. — Разве могут аксиомы Лобачевского выполняться в геометрии
Евклида?
Оказывается, могут. Дело в том, что в роли основных понятий геометрии
Лобачевского выступают не обычные точки, прямые, перемещения евклидовой
геометрии, а более специальные понятия. Для задания модели, таким образом,
используется своего рода «словарь» — перечень основных понятий геометрии
Лобачевского и их «перевод»: соответствующие специальные понятия из выбранной
части евклидовой геометрии».
Откровенно говоря, ученые не
очень стесняются или вообще не стесняются впадать в настоящий парадокс в стремлении как можно быстрее и
полнее формализовать то, что формализовать, вообще говоря, не так-то просто и
удобно, ведь приходится формализовывать то, что формы не имеет – бесконечное, аформальное. Дело ведь как раз в том,
что получаемые таким образом – «методом формального
нарекания геометрической курицы – геометрическим карпом» – евклидовые, то
есть чисто формальные модели подчиняющиеся строго формальной логике уже не являются таковыми, ибо самой формальной логикой переводятся в пространство
действия логики аформальной (диалектической).
Итак, смотрим:
«Оказывается (мы это подробнее проверим ниже), что при таком толковании
слов «точка», «прямая», «плоскости», «перемещение плоскости» выполняются все
аксиомы геометрии Лобачевского. А это как раз и значит, что
геометрия-Лобачевского — непротиворечива. - Почему? Вот как это объясняет сам
автор модели, Анри Пуанкаре:
«Возьмем теоремы Лобачевского и переведем их с помощью нашего словаря,
как мы переводим немецкий текст на французский язык с помощью
немецко-французского словаря. Мы получим, таким образом, теоремы обыкновенной
геометрии. (...) Стало быть, как бы далеко мы ни развивали следствия из
допущений Лобачевского, мы никогда не натолкнемся на противоречие. В самом
деле, если бы две теоремы Лобачевского находились в противоречии, то то
же самое имело бы место и для переводов этих двух теорем, сделанных при помощи
нашего словаря; но эти переводы суть теоремы обыкновенной геометрии (...),
которая свободна от противоречий».
Это рассуждение показывает, что из
непротиворечивости евклидовой геометрии следует непротиворечивость геометрии
Лобачевского. Именно в этом смысле Пуанкаре говорил, что ни одна геометрия
не может быть более истинна, чем другая.
Таким образом, чтобы установить непротиворечивость геометрии
Лобачевского, осталось проверить, что все ее аксиомы выполнены для построенной
выше модели».
Мы не будем проверять
непротиворечивость геометрии Лобачевского, а отметим лишь противоречивость
самого «метода словаря», в котором весь математический интерес исчерпывается результатом перевода, а не пониманием
сути и смысла, т.е. процессом становления этого результата, в котором понятия
содержательно весьма отличные друг от друга становятся друг другом. Ведь результат таков (см.ниже), но что он
означает?
«В модели Пуанкаре в круге за плоскость Лобачевского принимается
внутренность круга (изображено на иллюстрации) в евклидовом пространстве;
граница данного круга (окружность) называется «абсолютом». Роль прямых выполняют
содержащиеся в этом круге дуги окружностей
 ,
перпендикулярных абсолюту, и его диаметры; роль движений — преобразования,
получаемые комбинациями инверсий относительно окружностей, дуги которых служат
прямыми».
,
перпендикулярных абсолюту, и его диаметры; роль движений — преобразования,
получаемые комбинациями инверсий относительно окружностей, дуги которых служат
прямыми».
Едва ли «круг» - это
«плоскость», и если плоскость, то
весьма своеобразно обрезано-оконеченная, причём к «плоскости Лобачевского»
относится именно только внутренность «круга-абсолюта»,
а не сам круг, т.е. точки собственно границ круга. «Прямые» тоже весьма
своеобразные, по школьному говоря «очень кривые прямые»….
Аналогичная и тоже достаточно
странная картина является познающему
взору если мы возьмём модель Ф.Клейна, которую мы уже ранее видели:

«Прямые» являют собой
отрезки, концевые точки которых однако не принадлежат прямой, а «плоскость»
также – некий круг граница которого не принадлежит пространству плоскости
Лобачевского.
«Модель
Клейна — модель геометрии Лобачевского. Эта модель была предложена
Бельтрами, наряду с моделью Пуанкаре. С её помощью возможно доказать
непротиворечивость геометрии Лобачевского в предположении непротиворечивости
Евклидовой геометрии.
Плоскость Лобачевского представлена в этой модели внутренностью
некоторого круга («абсолюта»). Точки абсолюта, называемые также «идеальными
точками», плоскости Лобачевского уже не принадлежат. Прямая плоскости
Лобачевского — это хорда абсолюта, соединяющая две идеальные точки.
Движениями геометрии Лобачевского в модели Клейна объявляются
проективные преобразования плоскости, переводящие абсолют в себя. Конгруэнтными
считаются фигуры внутри абсолюта, переводимые друг в друга такими движениями.
Если точки A и B лежат на хорде PQ так, что порядок их следования
на прямой PABQ, тогда расстояние
 в
плоскости Лобачевского определяется как
в
плоскости Лобачевского определяется как
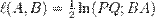
где (PQ;BA) обозначает двойное
отношение.
Любой факт евклидовой геометрии, описанный на таком языке, представляет
некоторый факт геометрии Лобачевского. Иными словами, всякое утверждение
неевклидовой геометрии Лобачевского на плоскости есть не что иное, как
утверждение евклидовой геометрии на плоскости, относящееся к фигурам внутри
круга, пересказанное в указанных терминах. Евклидова аксиома о параллельных
здесь явно не выполняется, так как через точку O, не лежащую на данной
хорде a, проходит сколько угодно не пересекающих её хорд».
Как отмечено, математиков
такие мелочи, как правило, не очень
смущают или попросту вообще не смущают, а нас же интересует именно то, что
объединяет все эти формально противоречивые, то есть противоречивые по форме, но единые в сути понятия, нас интересует процесс их превращения друг в друга.
Интересно кроме всего прочего, что нередко истина указанного рода отношений спокойно декларируется тут же, так сказать в одной формально
определённой геометрической куче:
«Одно из преимуществ модели Пуанкаре состоит в том, что на ней — с нашей
евклидовой точки зрения — можно увидеть таинственное множество «бесконечно
удаленных» точек геометрии Лобачевского.
Покажем, что граничную окружность у естественно рассматривать как
«бесконечно удаленную окружность» плоскости Лобачевского К. Для этого
возвратимся ненадолго в обычную евклидову плоскость и посмотрим, как с помощью
перемещений евклидовой плоскости сдвинуть заданную фигуру сколь угодно далеко
от ее первоначального положения».
Отметим, что на странной
плоскости-круге модели Пуанкаре можно обнаружить нечто в виде «таинственного множества «бесконечно
удаленных» точек геометрии Лобачевского», но чтобы видеть это нечто необходимо узнать кое-что дополнительное, без чего
логика существования самой модели так и останется покрытой глубоким геометрическим
мраком.
Прежде всего, нам необходимо
понять, что такое «инверсия».
Это понятие не является для
нас совершенно новым.
Пришла пора узнать подробно, что это такое.
«Инверсией (О, r)
(или симметрией относительно окружности с центром О и радиусом r) называется преобразование
плоскости, при котором каждой точке М ставится в соответствие такая точка М' на
луче ОМ, что
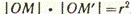 .
.
Точку О называют центром инверсии (это единственная точка, где
преобразование не определено), число r — радиусом инверсии, а окружность (О, r) — окружностью инверсии.
Инверсия — действительно своего рода симметрия относительно окружности;
она «выворачивает» внутренность окружности в ее внешность (и наоборот),
своеобразно искажает форму и размеры фигур (см. иллюстрации к статье «Инверсия»
в «Кванте» №. 5, с. 26). Основные свойства инверсии (О, R) показаны на рисунке
2, где можно проследить, что
1) точки, лежащие внутри окружности инверсии, переходят в точки, лежащие вне нее, и наоборот;
2) точки окружности инверсии, и только они, остаются
на месте;
3) прямые, проходящие через центр
инверсии, переходят в себя;
3') прямые, не проходящие через центр инверсии, переходят в окружности;
4) окружности, проходящие через центр инверсии, переходят в прямые;
4') окружности, не проходящие через центр инверсии, переходят в
окружности;
5) величина углов между линиями
сохраняется;
6) инверсия, как и другие виды
симметрии, обратно самой себе; другими словами, двукратное применение инверсии возвращает
все точки (кроме О) на место.[…]
7) Любая окружность, ортогональная
окружности инверсии, переходит в себя при этой инверсии».
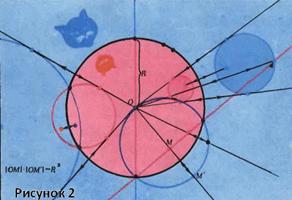
Внимательно всмотримся в
рисунок 2, где достаточно наглядно показано, что такое инверсия относительно
окружности радиуса r.
Возможно, остался открытым вопрос о том, что такое
ортогональность.
«Назовем две линии — окружности или прямые — ортогональными, если они
пересекаются под прямым углом. … под углом между двумя окружностями понимается
угол между касательными, проведенными к ним в точке пересечения. Заметим, что
прямая, ортогональная окружности, обязательно проходит через ее центр, а
касательная к одной из двух ортогональных окружностей в точке их пересечения
проходит через центр другой (рис. 1).»
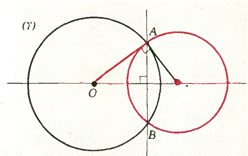 Рис.1
Рис.1
Итак, «одно из преимуществ модели Пуанкаре состоит в том, что на ней — с
нашей евклидовой точки зрения — можно увидеть «нечто таинственное» - «бесконечно
удаленные» точки геометрии Лобачевского.
Покажем, что граничную окружность γ естественно рассматривать как «бесконечно удаленную окружность» плоскости
Лобачевского λ. Для этого возвратимся ненадолго в обычную евклидову
плоскость и посмотрим, как с помощью перемещений евклидовой плоскости сдвинуть
заданную фигуру сколь угодно далеко от ее первоначального положения. Например,
это можно сделать так. Выберем на евклидовой плоскости две параллельные
несовпадающие прямые l1, l2 и отразим плоскость симметрично относительно прямой l2. Тогда прямая l1,
перейдет в прямую l3.
Отразим плоскость симметрично относительно l3, обозначим l4
образ прямой l1, при
этом отображении. Продолжая дальше этот процесс, получим семейство параллельных
прямых. При отражении заданной фигуры относительно этих прямых
последовательность ее образов уходит в бесконечность (рис.6).
Аналогичное построение можно выполнить на плоскости Лобачевского λ.
Выберем две произвольные параллельные «прямые» m1, m2 и на каждом шаге вместо осевой симметрии будем производить
симметрию относительно окружности. В результате возникает семейство
ортогональных у окружностей. При последовательном отражении в них произвольная
фигура будет передвигаться все ближе и ближе к окружности γ (рис. 6).
Точки окружности γ, таким образом, играют роль бесконечно удаленных точек».
 Рис.6
Рис.6
Дабы принципиальные отличия «эвклидовой плоскости» и
«эвклидовой модели плоскости Лобачевского» было ещё нагляднее ниже на рисунке А1 и А2 представлены два решения задачи
замощения плоскости правильными треугольниками:
 Рис.А1
Рис.А1
 Рис.А2
Рис.А2
Понятно, что замощение
треугольниками плоскости на Рис.А1, так сказать, неоконченное и может быть бесконечно продолжено на все
три стороны.
А вот Рис.А2 показывает если
и не оконченное замощение пространства плоскости, то по крайней мере четко
очерчивает его границы, показывая диалектическую сущность
всякой границы.
Модель Пуанкаре показывает нам, наконец-то, в явном виде самую суть проблемы – «эвклидовой
модели плоскости Лобачевского» – она неевклидова и обладает знакомым нас
набором качеств аформального
пространственного объекта:
А) Граница пространство
плоскости Лобачевского является определенным
пределом геометрических форм, которые строят такое пространство;
Б) Пространство плоскости Лобачевского является
бесконечным;
В) Пространство плоскости Лобачевского,
являясь бесконечным пространством, охватывается как целое и имеет свою
форму-границу, которая, таким образом, одновременно и бесконечна и конечна.
Учитывая кроме сказанного эффекты инверсии, которые можно видеть
на рисунке далее, и понимая глубинную
идею инверсии как бесконечного, строящего самого себя рефлексивного основания,
в котором Абсолютная Точка Центра Инверсии проецируясь относительно Своих
Мнимых Форм порождает Пространства Проекций, являющиеся подобиями Центра
Инверсии, можно подвести некоторый итог проективно-неевклидовым изысканиям.

Рис. Инверсия шахматной
доски относительно центра шахматной доски
Любая точка, лежащая на
окружности, относительно которой производится преобразование инверсии, при
отображении переходит в себя же. Любая точка, лежащая внутри окружности,
переходит во внешнюю область, и наоборот. Центр окружности переходит в точку
"бесконечность", а точка "бесконечность" — наоборот, в
центр окружности.
Указанный переход, в котором – и это очень важно – бесконечное становится (становится!) конечным, а конечное – бесконечным, порождая при этом и бесконечное
пространство, и пространственную границу, которая
определяет такое бесконечное пространство в его двуединой форме – точки и бесконечной
плоскости, является ещё одной наглядной математической моделью того, что
такое понятие.
Неевклидова (проективная)
геометрия – отрасль
математического знания, в которой в явной форме необходимым основанием
построения математических форм становится аформальное или бесконечное, т.е. как
бы «не имеющее формы» основание. Видимо не случайно такое основание было
названо «абсолютом». Конечно, это так сказать, не настоящий абсолют, и более
того – вовсе даже не абсолют, но лишь
начало движения к нему, в котором, однако же, ещё по сути отсутствует непосредственный переход и движение от
одной формы к другой, но лишь результат такого
движения.
В математике т.н. «абсолют» появился
в тот момент, когда неподвижные
евклидовы геометрические формы познающий
субъект смог развернуть в бесконечность, и математическое (геометрическое)
пространство стало, наконец, на деле пространством
бесконечным, но таким бесконечным, которое было охвачено математическим разумом в качестве целого:
«Проективная геометрия является наиболее удобным исходным пунктом для
объяснения сущности не только геометрии Лобачевского, но и широкого круга
других геометрических систем, возникновение которых связано с именем Феликса
Клейна, с идеями теории групп преобразований. Именно, при помощи методов
проективной геометрии, обходясь относительно простым математическим аппаратом,
можно описать девять хорошо известных в науке неевклидовых геометрий плоскости
и показать возможность их применения в физике. Решающую роль в таком описании
играет понятие абсолюта, т. е. некоторой фигуры, заданной на проективной
плоскости и остающейся неизменной при всех преобразованиях некоторой подгруппы
группы проективных преобразований».
Проективная геометрия и
проективное пространство первоначально появились как результат простого
дополнения обычных евклидовых пространственных форм, так называемыми, несобственными элементами – т.е. бесконечно
удалёнными точками, прямыми и плоскостью:
«При этом каждая прямая дополняется одной несобственной точкой, каждая
плоскость — одной несобственной прямой, всё пространство — одной несобственной
плоскостью; параллельные прямые дополняются общей несобственной точкой,
непараллельные — разными; параллельные плоскости дополняются общей
несобственной прямой, непараллельные — разными; несобственные точки,
дополняющие всевозможные прямые данной плоскости, принадлежат несобственной
прямой, дополняющей ту же плоскость; все несобственные точки и прямые
принадлежат несобственной плоскости».
Выявление такого
бесконечного (аформального) математического
основания как этапа движения к абсолютному основанию закономерно не могло
не привести к эффекту универсализации математического знания,
множество математических форм «вдруг» в себе обрели нечто такое, из чего все
эти формы могут быть выведены. Более того, при этом даже сама форма математического
мышления приобретает особые объединяющее-систематизирующие черты…
И здесь, по-видимому, стоит немного
остановиться на т.н. «Эрлангерской программе» Феликса Клейна, в которой
собственно и проявилось то особое качество мышления, которое сам Клейн
определил как «проективное»…
«— Милостивые государи! Между приобретениями, сделанными в области
геометрии за последние пятьдесят лет, развитие проективной геометрии занимает
первое место.
Если в начале казалось, что для нее недоступно изучение так называемых
метрических свойств, так как они не остаются без изменения при проектировании,
то в новейшее время научились представлять и их с проективной точки зрения, так
что теперь проективный метод охватывает всю геометрию...
Так начал Феликс Клейн свою первую лекцию, которая не только обеспечила
ему право на кафедру в Эрлангене, но и открыла дорогу в бессмертие. Через
двадцать лет, будучи уже маститым ученым, профессором Геттингенского
университета и редактором крупнейшего в мире журнала «Mathematische Annalen»,
Клейн вновь опубликовал текст этой лекции, снабдив его подробными дополнениями
и пояснениями. Именно этот текст и стал «каноническим» вариантом «Эрлангенской
программы», именно он и переведен на все языки мира.
Сущность и значение «программы» Клейна наиболее кратко и выразительно
сформулировал его ученик и последователь, известный немецкий геометр Вильгельм
Бляшке: «От него (т.е. от Клейна) ведет начало геометрическое мышление,
базирующееся на рассмотрении непрерывных групп преобразований, а этот образ
мыслей является основой всего дальнейшего». Большая часть Эрлангенской
программы как раз и посвящена теории этих групп, на основе которой и
сравниваются «новейшие геометрические исследования», производится классификация
геометрических фактов и теорий.
Что же такое «непрерывная группа преобразований»?
Каждое из трех слов в отдельности — «непрерывность», «группа»,
«преобразование» — попятно любому человеку и вроде бы не содержит ничего
специального, математического. Но их соединение в обычной речи не встречается,
это уже чисто математический термин, более того, важнейший термин современной
математики. Попробуем разобраться в нем, так сказать, «по порядку».
«Преобразование». Под этим словом понимается почти то же, что и в
обычной жизни. Кстати, наш читатель, наверняка не забыл симметрию, параллельный
перенос, гомотетию. Мы подробно описывали проектирование: при этом
преобразовании одна фигура превращается, преобразуется в другую, более того,
вся плоскость, содержавшая проектируемую фигуру, также подвергается
преобразованию — все ее точки проектируются в точки другой плоскости,
«плоскости проекций». Теория таких преобразований является научной основой
живописи, начертательной геометрии, фотографии, кинематографии, аэрофотосъемки,
картографии и т.д.
Когда говорят о группе
преобразовании? Очевидно, тогда, когда речь идет не об одном
преобразовании, а о нескольких, о множестве (конечном или даже бесконечном). В
математике группа преобразований — это не любое множество преобразований, а
множество, обладающее определенными свойствами.
Главное свойство заключается в том, что двукратное (следовательно, и
многократное) повторение преобразований из этого множества может быть заменено
одним преобразованием из этого же множества, причем результат окажется тем же
самым. В главе третьей мы видели, что обычные проектирования (перспективы) не
обладают таким свойством, — следовательно, множество проектирований не является
группой. Но проективные преобразования, характеризующиеся сохранением сложного
отношения четырех точек, уже обладают этим свойством: результат двух
проективных преобразований снова дает проективное преобразование, так как все
сложные отношения по-прежнему останутся неизменными.
Нам осталось объяснить последнюю часть термина «непрерывные группы
преобразований» — эпитет «непрерывные».
Понятие непрерывности интуитивно сопоставляется с геометрическим образом
— непрерывной линией. Линии же мы привыкли связывать с графиками функций:
синусоида есть график функции у = sinх, парабола — график функции у = х2,
кубическая парабола — график функции у = х3 и т. д. Все эти графики
представляют собой непрерывные кривые. Естественно, что и соответствующие
функции называются непрерывными.
Перенести это хорошо известное понятие на группы преобразований нетрудно
— надо лишь научиться задавать преобразования аналитическими формулами, так же,
как мы задаем кривые уравнениями. В следующих главах мы познакомимся с
некоторыми примерами непрерывных групп преобразований.
Разработанная Клейном в многолетнем сотрудничестве с норвежским
математиком Софусом Ли (1842—1899) теория непрерывных групп преобразований
(теперь их часто называют «группами Ли») стала основой классификации в
геометрии.
Идея Клейна состоит в том, что признаком, определяющим принадлежность
геометрического факта (свойства фигуры, геометрической величины и т.д.) тому
или иному разделу геометрии, является его сохранение, инвариантность при любом
преобразовании данной непрерывной группы. Значит, каждой непрерывной группе
преобразований соответствует вполне определенная часть геометрии. В дальнейшем
каждую такую часть стали называть просто геометрией с эпитетом, указывающим на
группу. Например, часть геометрии, соответствующая группе проективных
преобразований, есть проективная геометрия.
Итак, классификация «геометрий» сводится к классификации непрерывных
групп. Трудность реализации идей Клейна состояла в том, что вопрос о самой
классификации непрерывных групп тогда еще не только не был решен, но даже и не
был поставлен. Этот вопрос в основном был решен в XX веке знаменитым
французским математиком Эли Картаном (1869—1951), получившим за исследования по
геометрии и теории групп премию имени Н. И. Лобачевского. Однако Клейн имел
основания надеяться, что такая классификация возможна и что она относительно
проста. В чем же состояли основания надежды Клейна? По работам Камиля Жордана (1838—1922)
и особенно в результате общения с Софусом Ли Клейн хорошо знал, что понятие
группы позволило пролить свет на самые различные и самые трудные проблемы
математики. Именно в книге Жордана «Трактат о подстановках и алгебраических
уравнениях» было изложено гениальное открытие безвременно погибшего Эвариста
Галуа (1811—1832), показавшего, что из всех алгебраических уравнений только
уравнения не выше четвертой степени всегда могут быть «решены в радикалах»,
т.е. по формулам, аналогичным известной формуле для квадратного уравнения.
Более того, Галуа указал способ, дающий возможность узнать, разрешимо ли в
радикалах то или иное конкретное алгебраическое уравнение пятой или более
высокой степени.
Эта задача, мучившая многие поколения математиков, была решена
двадцатилетним юношей Галуа при помощи созданной им теории «групп подстановок»
— теории удивительно глубокой, достойной создавшего ее гения».
Но нас по понятным разумозрительным
причинам интересуют, прежде всего, такие проективные
качества, которые позволяют любому, вставшему на дорогу познания диалектических
тайн, наглядно увидеть пространственно-геометрическую интерпретацию диалектических парадоксов, или, по
крайней мере, выявить подобие аформальных
форм, лежащих в основе таких парадоксов. Пример кольца Мёбиуса (по
количеству фактических упоминаний) должен быть уже видимо, назван хрестоматийным.
Двумерное проективное
пространство называется проективной плоскостью.
Вспомним, что в Третьей Главе уже было анонсировано
наблюдение Б.Римана о том, что из неограниченности пространства ещё не следует
его бесконечность:
«В 1854 Б. Риман (1826-1866) заметил, что из неограниченности
пространства еще не следует его бесконечная протяженность. Смысл этого утверждения станет яснее, если представить, что в
неограниченной, но конечной вселенной астроном в принципе мог бы увидеть в
телескоп, обладающий достаточно высокой разрешающей способностью, свой
собственный затылок (если отвлечься от небольшой детали, связанной с тем, что
свет, отраженный от затылка, достиг бы глаза астронома через тысячи миллионов
лет). В своем доказательстве того, что внешний угол при любой вершине треугольника
больше внутреннего угла при любой из двух остальных вершин, Евклид неявно
использовал бесконечную длину прямой. Из этой теоремы тотчас же следует теорема
о том, что сумма любых двух углов треугольника меньше суммы двух прямых углов.
Если отказаться от бесконечной длины прямой, то гипотеза Саккери о тупом угле
становиться верной и из нее следует, что сумма углов треугольника больше суммы
двух прямых. Такое положение дел было давно известно в сферической
тригонометрии, где стороны треугольника являются дугами больших кругов. Риман внес эпохальный вклад, распространив
представление о конечном, но неограниченном пространстве с двух на три и
большее число измерений.
Эллиптическая плоскость. Ф.Клейн (1849-1925) первым увидел, как избавить
сферическую геометрию от одного из ее недостатков - того, что две лежащие в
одной плоскости "прямые" (два больших круга на сфере) имеют не одну
общую точку, а две (рис. 3,а). Так как для каждой точки существует
одна-единственная точка-антипод (диаметрально противоположная точка), а для
любой фигуры существует ее дубликат из точек-антиподов, мы можем, ничем не
жертвуя, но многое приобретая, абстрактно
отождествить обе точки такой пары, объединив их в одну. Таким образом можно
изменить смысл термина "точка", условившись впредь называть
"одной точкой" пару диаметрально противоположных точек. Иначе
говоря, точки так называемой "эллиптической" плоскости представлены
на единичной сфере парами точек-антиподов или диаметрами, соединяющими
точки-антиподы».
а - на эллиптической плоскости "точка" представлена двумя
точками-антиподами на сфере, например, точками P и P'. б - диаметр, соединяющий
северный и южный полюсы сферы, на эллиптической плоскости является
"полюсом" экватора».
Такое
представление с помощью диаметров и диаметральных плоскостей сферы (при котором
диаметр, соединяющий северный и южный полюсы сферы, является
"полюсом" экватора), показывает, что все свойства действительной
проективной плоскости сохраняются и для эллиптической плоскости.
Обратим внимание на то, что отношение форм, порождая из себя
нечто, выходящее за границы формального отношения, а для этого необходим сам
факт наличия аформального в общем виде, т.е.бесконечности, тут же оформляет это
неформальное отношение, например, в некоторой аформальной форме, в форме в буквальном смысле непредставимо-удивительной
сферы, в которой точки попарно тождственны друг другу.
Воистину было бы интеллектуальным грехом, если бы такой
аформализм что называется «пропал зря» в философской сфере как яркая модель
диалектического отношения, в котором двойственность и противоположность,
символизируемая парами точек, которые образуют форму сферы Римана, не означала
бы одновременно того, что точки
эти попарно тождественным друг другу и факт тождества всовокупности являет
собой особую и воистину непредставимую
форму, с которой однако легко, непринужденно и продуктивно работают
математики и физики.
Сфера Римана одновременно являет собой так называемое расширение комплексной плоскости, что
для нас по понятным причинам весьма значимо.
Одно из интересных и важный свойств проективной
плоскости, интересных и важных как раз
потому что эти свойства парадоксальны – это то что проективная плоскость демонстрирует самое существенное свойство
понятия.
Вспомним (Третья Глава):
«… любое понятие является антиномией – воплощенным противоречием двух своих сторон,
а точнее пространств, пространств симметричных относительно замкнутой
границы, являющейся границей понятия:
А) содержательно объем понятия
является неограниченным и может свободно расти именами форм содержания понятия, таково «внутреннее» пространство
понятия и оно в своем роде может быть названо бесконечным (если быть формально
точным – безграничным);
Б) формально – т.е. именем формы понятия, содержательность которого может свободно и неограниченно возрастать, вся эта потенциальная и
актуальна неограниченность охватывается
извне пространства содержательности понятия, и таково «внешнее»
пространство понятия;
С) оба эти пространства, как
«внешнее», так и «внутреннее» являются одним и тем же пространством.
В любом обобщающем понятии в
действительности происходит процесс
отождествления понятий в соответствии с общей формулой: «единичное (особенное)
есть особенное (общее)» или «единичное есть общее (всеобщее)».
Итак, как же получается сфера Римана?
Очень просто:
На плоскости находится сфера, которая касается плоскости в
точке S. Из точки N противоположной точке S мы
осуществляем проецирование, в результате которого каждой точке сферы ставится в
соответствие точка плоскости (z z’).
Можно видеть, что при проецировании бесконечно близкая
окресность точки N и сама точка N составляют соответственно: бесконечно удаленную окресностью бесконечно
удаленной границы комплексной плоскости. Проецирующая прямая в этом случае
перпендикулярна диаметру сферы SN и паралллельна плоскости.
Что такое проективная
плоскость с точки зрения нашего трехмерного пространства (в качестве примера
процесса оформления того, что на первый взгляд не может иметь никакого здраво представимого
оформления)?..
«Проективная плоскость (аббревиатура RP
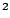 , real projective plane) -
это множество всех прямых в трёхмерном пространстве, проходящих через начало
координат (рис.а).
, real projective plane) -
это множество всех прямых в трёхмерном пространстве, проходящих через начало
координат (рис.а).
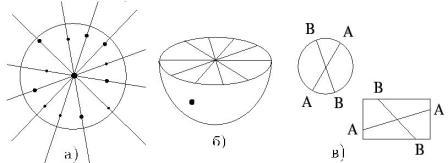
Рис.5.1.Эквивалентные определения
проективной плоскости.
Каждая прямая однозначно определяется своим
пересечением со сферой с центром в начале координат, однако противоположные
точки сферы определяют одну и ту же прямую. Поэтому другой моделью проективной
плоскости является сфера в трёхмерном пространстве, на которой пары
противоположных точек отождествлены, т.е. рассматриваются как одна точка. Мы
всегда можем считать, что эта сфера отображена куда-нибудь, например снова в
трёхмерное пространство, используя отображение, которое действительно склеивает
противоположные точки в одну. При этом мы получаем модель проективной
плоскости, представляющую её как поверхность в трёхмерном пространстве. Для
представления проективной плоскости достаточно использовать только полусферу и
принять во внимание то, что противоположные точки на её экваторе должны быть
отождествлены (рис.б). Топологически полусфера эквивалентна диску (или
прямоугольнику), поэтому проективная плоскость может быть определена как
результат склеивания противоположных точек на границе диска (рис.в).
Рис.5.2.Два метода сборки проективной
плоскости.
Попробуем построить эту поверхность в трёхмерном пространстве, используя
последнее определение. Возьмём эластичный диск (рис.а), потянем друг к другу
противоположные стороны диска, скрутив одну сторону, как показано на рисунке, и
склеим сомкнутые участки. Продолжим склеивание влево и вправо вдоль границ поверхности.
На последнем этапе склейки мы встретим одно топологическое препятствие:
скрученную ленту, которая мешает нам сомкнуть отверстие. Смыкая отверстие
сквозь ленту, мы получим модель проективной плоскости. Описанное препятствие
показывает, что проективная плоскость не может быть вложена в трёхмерное
пространство, т.е. представлена как гладкая поверхность без самопересечений.
Проективная плоскость обладает двумя свойствами:
1. она замкнута - не имеет границы, подобно сфере;
2. она неориентируема - имеет одну сторону, подобно бутылке Клейна.
Существует общая топологическая теорема [57],
запрещающая вложение замкнутых неориентируемых поверхностей в трёхмерное
пространство. Таким образом, мы вынуждены смириться с самопересечениями, имея в
виду, что каждая точка на самопересечении представляет две точки проективной
плоскости.
Другой топологически регулярный способ представления поверхностей
называется погружением. Погруженные поверхности могут иметь самопересечения, но
не должны иметь особых точек. В каждой точке погруженной поверхности должны
существовать касательная плоскость и нормальный вектор. Иначе говоря, в
окрестности каждой точки поверхность должна выглядеть как слабо искривлённый
диск, за исключением точек на линии самопересечения, где поверхность должна
выглядеть как несколько пересекающихся дисков. В силу другой общей
топологической теоремы (теоремы Уитни), любая поверхность может быть погружена
в трёхмерное пространство. На рис.б показан другой способ построения
проективной плоскости. Как мы уже говорили, проективную плоскость можно
определить как прямоугольник с отождествлёнными противоположными точками на
границе. Разделим прямоугольник на три части, как показано на рисунке рис.. Из
верхней и нижней частей склеим диск, а из центральной части - ленту. Поскольку
эта лента должна быть скрученной (см.рис.рис.б), это - лента Мёбиуса. Её
граница является одной (связной) кривой, как и для диска. Нам осталось только
склеить ленту Мёбиуса и диск вдоль их границ. Подробнее мы опишем этот процесс
в конце данного подраздела. Полученная в итоге поверхность называется
скрещённым колпаком. Это одно из возможных изображений проективной плоскости в
трёхмерном пространстве.
Скрещённый колпак является неориентируемым, подобно бутылке Клейна и
ленте Мебиуса (последняя, по построению, содержится в скрещённом колпаке).
Поместив малый объект на поверхность и перемещая его по определённому
замкнутому пути, мы можем получить объект с обратной ориентацией. Таким
образом, на поверхности невозможно задать глобальную ориентацию. Мы можем легко
продемонстрировать это свойство поверхности, используя анимацию.
Поскольку скрещённый колпак имеет самопересечение, эта поверхность не
является вложенной. Как уже отмечалось, вложения проективной плоскости в
трёхмерное пространство не существует. Скрещённый колпак также обладает
особенностями специального вида, которые называются точками пинча. Поверхность
вблизи точек пинча не выглядит как несколько пересекающихся дисков, а обладает
более сложной структурой. В частности, она не является здесь гладкой: в этих
точках не существует касательной плоскости и нормального вектора к поверхности.
Таким образом, скрещённый колпак не является погруженной поверхностью.
В силу теоремы, упомянутой выше, погружение проективной плоскости в
трёхмерное пространство существует. Это погружение было построено Вернером Боем
в 1900 году, но его явное аналитическое представление было найдено Фрасуа Апери
только в 1987 году. Поверхность Боя имеет линию самопересечения в виде трёх
петель, связанных в одной точке (узле). В действительности это одна гладкая
замкнутая кривая (топологическая окружность), которая пересекает себя в этом
узле. Узел является тройной точкой поверхности. Вблизи узла поверхность
выглядит подобно трём пересекающимся плоскостям».
Этим мы, наконец и завершим наш долгий путь выявления в
математике того, что роднит её с гегелевской философией и её бессмертным
методом.
Будем считать процесс окантовки диалектики завершенным, как будем
считать завершенным этап рассмотрения Теории
предстоящей Практики, той Практики
которая станет условием воплощения Коммунистического Будущего человечества.
Рассматриваемая нами Теория является научно-обоснованным необходимым
основанием, т.е. Всеобщей Точкой Зрения,
которая одновременно есть и Точка Зрения Всеобщего,
при этом мы не будем вновь даже поднимать
вопрос о том, в какой мере «Всеобщее» может быть обозначено понятием «Бог»
или «Всевышний»…
Видящий Глазами Всеобщего –
видит Истину.
А Истина эта… воистину неожиданна
и страшна.
Но иной не будет. И это нужно принять.
Мы переходим ко Второй Части
Книги помня при этом, что задача
Первой Части Книги заключалась в том, чтобы вопреки существующему торжеству
тотальности слабоумия донести истину знания до тех, кто в нем
нуждается более чем в чем-либо другом.
Часть Вторая продолжит дело Первой.
Как мы рассчитываем это сделать?
Можно сказать «как всегда», т.е.: через
развенчание тупости и не взирая на лица, через очищение авгиевых конюшен
философии и науки, через раскрытие и познание глубочайших основ философского
мышления, через утверждение этих
философских основ, заложенных признанными гениями и выдающимися мыслителями
человечества, через кардинальный пересмотр самых
прочных стереотипов и утверждение самых парадоксальных и кажется совершенно
немыслимых вещей…
О чём конкретно пойдёт речь?
А) речь идёт именно о Научной Теории, истинно-научной Теории Трансформ-марксизма, истинной потому что
универсальной и всеохватной, обладающей той
же мерой всеобщности, что и философская концепция Ф.Гегеля, которая
является центральным стержнем этой
Теории;
Б) общий
каркас Теории Трансформ-марксизма – это кардинально
пересмотренная и очищенная от глупостей и потому принципиально улучшенная
широко известная теория марксизма,
включая и ту её версию, которая была дана Владимиром Ульяновым (Лениным), и
которая как это ни покажется невероятным до настоящего момента совершенно не известна ни широкой читательской
аудитории, ни в ученых (академических) кругах;
В) содержанием-наполнением Теории Трансформ-марксизма является много-
и разнообразное теоретическое и практическое приложение Теории на самом
различном материале, в том числе и уже показанном в Первой Части
(на примере математики и её форм) учебного материала;
Г) особо,
а в ряде случаях абсолютно значимым является уже наработанные на основе Теории Трансформ-марксизма ряд практически готовых к применению и
воплощению целостных и согласованных друг с другом по всем
социально-иерархическим уровням моделей (проектов) строительства будущего
общества, которые призваны стать единой общемировой моделью развития.
Ч. Мизнер, К. Торн, Дж. Уилер «Гравитация» том 3 Пер. с англ.
А. Г.Полнарева под ред. Б. Б. Брагинского и И. Д. Новикова изд. «Мир» М. 1977
Что касается «товарища Сталина» то сразу можно было бы кое-что
отметить, дабы вновь не сработал указанный обывательский рефлекс. Как философ и ученый «Сталин» даже не дотягивает до уровня тяжеловесно-бестолкового горбачевского
«нового мышления», которым Горби так
непоправимо загрузил советское мышление,
что в нём что-то с хрустом сломалось. Хотя, кто знает, может быть, схожесть
звучания «загрузить» и «загрузинить» вовсе и не случайна, судя по тому, что
гордая «грузинскость» на деле оказалась саакашлоидностью темного пресмыкания. И
сказанное вовсе не является некоей
«эмоциональной оценкой», которые так модны сейчас, когда можно говорить что
душе угодно, и которые выставляют как раз те, у кого за душой нет ни единой
своей мысли, но обязательно есть свой убогий скрюченный интерес, который и принимает самые немыслимые вербальные формы при
любом удобном случае.
Итак, во Второй Части
Книги будет показано и доказано, что
Сталин если и обладал гениальностью, то единственной и особой. Сталин –
гениальный тиран, во всём же ином он посредственность, порой просто до смешного
слабоумная. Что касается остальных упомянутых персонажей, от которых нынешних
философов начинает корчить, то с ними не всё так просто, как хочется обывателю,
вкусившему буржуазных прелестей, пусть даже у него в шкафу лежит выданный
соответствующей инстанцией документ о том, что он «философ» и потому видимо
«мыслитель».
И хотя Маркс и Ленин
кое в чём и очень существенном ошибались, но в отличие от революционного недоумка
«Сталина», эти настоящие революционеры Истории действительно были гениями, в том числе и как ученые. Но вот «марксисты», «ленинцы», а также «марксисты-ленинцы»
на их фоне выглядят, если выразиться бесконечно деликатно – инициативными
даунами, а такие вещи необходимо знать.
Вот тут-то с учетом
указанного знания и возникает вполне правомерные вопросы: а при чём же здесь
те, чьими именами прикрывались те проходимцы, которые умело, и лишь для
малограмотных масс убедительно рядились в коммунистические мундиры и паразитировали
на всех тех, кто не мог мыслить и не понимал происходящего? И, главное, что при
этом делали все те, кто обязан был понимать и быть мыслителем, просто потому что назвались таковыми?
Вейль Герман «О философии
математики: Пер. с нем. / Предисл. .А.Яновской. Вступ. ст.А.П.Юшкевича.
Изд.2-е, стереотипное. — М.: КомКнига, 2005. — 128 с., с.9-12
На
геометрический манер — лат.
Гегель Г.В.Ф. Энциклопедия философских наук. Т. 1.
Наука логики. М., «Мысль», 1974.-452 с.- (Филос. Наследие. Т.63).-С.53-424с
примечаниями; с. 134-135
Гегель Г.В.Ф. Энциклопедия философских наук. Т. 1.
Наука логики. М., «Мысль», 1974.-452 с.- (Филос. Наследие. Т.63).-С.53-424с
примечаниями; с. 134-135
Все фрагменты из Г.В.Ф. Гегель «Наука логики». -
Спб., - 1997. Жирный шрифт - Наш
А ведь дурость как известно даже
последнему дураку – не лечится, хотя и заразна как бубонная чума, что известно
очень немногим умным (Вспоминая М.Задорнова…)
Вейль Г. «Топология и абстрактная алгебра как два
способа понимания математики» (Доклад на Летней школе (Ferienkurs),
организованной швейцарским Обществом преподавателей гимназий в Берне; 10.1931
г.) Источник: Вейль Г. МАТЕМАТИЧЕСКИЙ СПОСОБ МЫШЛЕНИЯ (под ред. Б.В. Бирюкова и А.Н. Паршина; пер.
с англ. Ю.А.Данилова). — М.: Наука, 1989. —стр. 24
Эл.ресурс URL:
http://www.i-u.ru/biblio/archive/veyl_topology/
Лосев А. Ф. «Хаос и структура» /Сост. А. А. Тахо-Годи и В. П.
Троицкого, общ. ред. А. А. Тахо-Годи и В. П. Троицкого.— М.: Мысль, 1997.— 831
с. («Математика и диалектика. К логическому обоснованию аксиоматики
трансфинитов») с.800-801
Единое – множественно, множественное – едино. Конечное – бесконечно,
бесконечное – конечно.
Количественное
– качественно, качественное –
количественно. Единое, единое как ОСНОВА, как сущность – формально и
поверхностно, поверхностное и форма – сущностны, и всё есть лишь переход…
М.Клайн «Математика Утрата определенности» Пер. с англ. Ю. А. Данилова под ред. д-ра
физ.-мат. наук, И. М. Яглома М. «Мир» 1984 с.174-175
Что уже нами наглядно рассмотрено на примере применения гипотетических
оптических приборов с бесконечным «увеличением» («уменьшением»).
Иначе говоря, лишь квадрат числа называемого «мнимой единицей»,
результат её умножение на себя имеет привычный числовой смысл.
Бинер «вера - знание» утверждает фактическое
равноправие полярностей, доминирование
одного (веры) соответствует законному периоду правильного, т.е.
соответствующего истине чувства-мироощущения
существование Всевышнего. Знание вырастает из веры, мысль – из чувств, переход
их друг в друга выражает нормальный процесс познания мира субъектом. По этой
причине «подвиг веры» который не отодвигает или просто игнорирует
противоречивость антиномии, а по-своему снимает её. Верить, как ни странно
намного сложнее, чем знать, знание – лишено чувственного, по крайней мере
такого без которого вера не может существовать – постоянного удерживания в
фокусе полноты горения пламени чувства сопричастности сверхчеловеческого бытия.
Флоренский П.А. У водораздела мысли. М., 1990, с.225
Флоренский П.А. У водораздела
мысли. М., 1990, с.292
«Делители нуля Пусть
— произвольное кольцо. Определение 1. Элемент
называется левым
делителем нуля1), если существует такой
, что
. Элемент
называется правым
делителем нуля2), если существует такой
, что
. Элемент
называется делителем
нуля3), если он является одновременно левым и правым делителем
нуля. Замечание 1. Если
— коммутативное кольцо, то левый делитель нуля
является правым делителем нуля и наоборот.
Пример 1. Пусть
— кольцо матриц порядка 2. Матрица
является делителем нуля, так как
А. Д. Александров «Тупость и гений» «Квант», №№11,
12, 1982
Хотя бы всем известного, но совершенно маловразумительного
и совершенно ничего не выражающего по рассматриваемой теме: «параллельные
прямые пересекаются»
Да нередко ещё не в одной
жизни, а во многих.
К тому же – как же похож этот философствующий медиатор на своих
отдаленных потомков которые сломя голову брались рассуждать о предметах в
которых они смыслили ещё меньше чем Чернышевский в геометрии! И разве не эти
интеллигентствующие потомки из социалистического
сна вытворяли такое, что ныне этот сон приобрёл в мире нерушимо твердую
репутацию кошмара?
Р. Н. Щербаков, Л. Ф. Пичурин «От проективной
геометрии — к неевклидовой (вокруг абсолюта): Кн. для внеклассного чтения. IX, X
кл. — М.: Просвещение, 1979.— 158 с, ил.— (Мир знаний).
Отсюда, например, всем известный школьный
идиотизм откровенной тавтологии «доказательства» от противного того, что
«параллельные прямые не имеют общей точки» - мол, «допустим, они параллельные
прямые пересекаются…»
Первичным является смысл, содержание, а не
форма. Форма есть результат движения содержания, результат оформления этого
движения самим содержанием. Интересен, прежде всего смысл перевода, а вовсе не
формальный результат в виде неких малопонятных начертаний-символов на некоем
языке…
Бесконечная она с точки зрения внутреннего
наблюдателя-обитателя пространства плоскости Лобачевского, а конечна с точки
зрения внешнего наблюдателя
Энциклопедия Кольера «НЕЕВКЛИДОВА ГЕОМЕТРИЯ»
Эл.ресурс URL: http://dic.academic.ru/dic.nsf/enc_colier/6335/НЕЕВКЛИДОВА
Так как мы уже знаем что такое комплексное число и число
вообще



